Машина тьюринга проверка на палиндром

Время работы алгоритма Дейкстры на машине Тьюринга

Машина Тьюринга как абстрактный исполнитель, вычислительная машина. Ее устройство и принципы управления, взаимосвязь элементов и назначение. Исследование отдельных палиндромических словосочетаний и фраз. Реализация проверки палиндрома на машине Тьюринга.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Размещено на http://www.allbest.ru/

3. Реализация проверки палиндрома на машине Тьюринга

4. Время работы алгоритма Дейкстры на машине Тьюринга

Устройство машины Тьюринга

В состав машины Тьюринга входит полубесконечная лента (возможны машины Тьюринга, которые имеют несколько лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.

Описание машины Тьюринга

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j>q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_j записывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (S)). Для каждой возможной конфигурации имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния (q₀), попав в которое машина останавливается.

Существуют разновидности, когда чтение производится не в обратном направлении, а в прямом, но с другого места в «размноженном» термине, например, кабанкабан, кольцокольцо, викивики. Такие «разночтения» могут встречаться и в ДНК.

3. Реализация проверки палиндрома на машине Тьюринга

тьюринг палиндром алгоритм

Построим машину Тьюринга, определяющую, является ли входное слово палиндромом. Алфавит машины: У = <0,1,>,?>.

Составим функцию переходов. Если лента пустая, то мы принимаем вход.

(q₀,?) > (q_yes. ·). Если лента не пустая, то мы запоминаем в состоянии первый символ (q₂, если это 0 и q₃, если это 1), заменяем его на > и перемещаемся к концу ленты.

Источник

Машина Тьюринга

Содержание

Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.

Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:

При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.

Определение [ править ]

Определение машины [ править ]

Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.

Определение процесса работы [ править ]

Особо следует рассмотреть случай переходов по пробельному символу:

Для машины Тьюринга, которая пишет символ [math]B[/math] на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.

Результат работы [ править ]

Примеры машин-распознавателей и машин-преобразователей будут даны ниже.

Примеры машин Тьюринга [ править ]

Прибавление единицы [ править ]

Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:

Проверка того, является ли слово палиндромом [ править ]

Варианты машины Тьюринга [ править ]

В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.

Многодорожечная машина Тьюринга [ править ]

Машина Тьюринга с полубесконечной лентой [ править ]

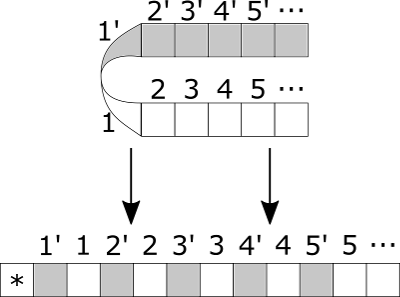
Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.

Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом:

Затем перенумеруем ячейки, и запишем символ [math]c \in \Pi \setminus \Sigma, B[/math] в начало ленты, который будет означать границу рабочей зоны:

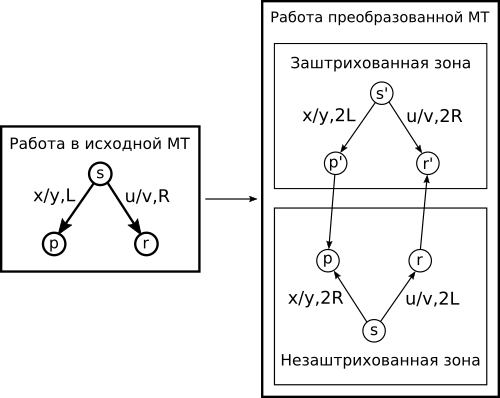
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации.[math]\triangleleft[/math]

Многоленточная машина Тьюринга [ править ]

Многоленточная машина с [math]n[/math] дорожками эмулируется многодорожечной машиной с [math]2n[/math] дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом [math]*[/math] позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).

Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов [math]*[/math] символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.

Аланом Тьюрингом было сформулировано следующее утверждение:

Иными словами, тезис говорит о том, что любой алгоритм можно запрограммировать на машине Тьюринга.

Универсальная машина Тьюринга [ править ]

Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, универсальный язык перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже.

Источник

Алгоритмы для поиска палиндромов

Сегодня я хочу вам рассказать об алгоритмах подсчёта количества палиндромов в строке: для чего это нужно, где применяется, как это быстро сделать, какие подводные камни нас ожидают и многое другое. Рассмотрим различные способы для решения данной задачи, выясним плюсы и минусы каждого способа. Эта статья будет обзорной: если я что-то не описываю здесь, то постараюсь всегда дать вам набор ссылок, где всё подробно описано и расписано. Надеюсь, что материал будет интересен как новичкам в сфере алгоритмов, так и матёрым программистам. Что же, если я смог заинтересовать вас, то прошу под кат!

Для начала стоит вспомнить, что же такое палиндром.

Палиндро́м — число (например, 404), буквосочетание, слово или текст, одинаково читающееся в обоих направлениях. Иногда палиндромом называют любой симметричный относительно своей середины набор символов.(выдержка из Википедии)

Определение очень лёгкое и понятное. Мы в данном посте будем рассматривать палиндромы-слова(поп, кок и т.д.). Но это не значит, что алгоритмы неприменимы для иных ситуаций. Просто чуть сузим область.

Для чего может потребоваться искать палиндромы?

На самом деле, не очень то и часто приходится искать палиндромы в повседневной жизни. Уж больно специфичная это задача. Если говорить о строковых алгоритмах, то мы намного чаще встречаем тот же поиск подстроки в строке, чем нахождение количества палиндромов. Поэтому и освещение в литературе намного слабее.

Одно из основных применений — спортивное/олимпиадное программирование. Там задач на такое хватает. Задач понаписывают, а участникам уже думай, каким способом это решить. Из личного опыта скажу, что мне такие задачи встречались всего пару раз, но все они были из разряда «вот тебе задача, ты не думай, а просто напиши алгоритм». То есть не интересные задачи, которые развивают просто механическую память по набиванию алгоритмов.

А более практическое применение нахождения палиндромов — это биологические алгоритмы. Согласно всё той же Википедии и ссылкам снизу Вики, палиндромность биологических соединений играет важную роль на свойствах различных биологических соединений. Я в биологии слаб, поэтому если вам интересно, то вы можете найти более подробную информацию сами.

Отлично, мы выяснили, что мы будем заниматься не совсем бесполезными делами. Давайте же уже перейдем к рассмотрению алгоритмов!

Замечание: во всех нижеприведённых алгоритмах одиночный символ не считается за палиндром. Как вы понимаете, это легко поправить, если одиночные символы тоже нужно будет учесть.

0) Самый банальный алгоритм с асимптотикой O(N^3)

Хочу предупредить сразу, что все исходники будут на C++, и это будут значимые части классов, которые нам могут быть интересны.

Алгоритм самый что ни на есть «лоб»: имеется строка, есть указатель на начало подстроки данной строки, есть указатель на конец данной подстроки. В двух вложенных циклах перебираем границы подстрок и банально проверяем, является ли наша подстрока палиндромом. Ничего сложного.

Но это всё ужасно медленно работает. Почему? Да потому что мы квадрат от N раз (N у нас будет всегда длина строки) перебираем границы текущей подстроки, а потом ещё и за O(N) в худшем случае выполняем проверку для каждой подстроки на палиндромность.

Плюсов у данного способа немного:

+ Легко реализуется. Действительно, оставить багу здесь ну очень сложно.
+ Легко читается. Вы только взглянули, и уже поняли, что да как здесь работает.
+ Малая скрытая константа. Как известно, на время работы алгоритма влияет не только асимптотическая оценка (здесь мы работаем только с худшими случаями), но и скрытая константа. У этого алгоритма скрытая константа крайне мала.

— Крайне малая скорость работы. Как вы можете видеть, что при строке из тысячи букв ‘a’ данный алгоритм сделает порядка 10^9 итераций, что есть очень плохо. А что если строка длиной 100000?

1) Самый банальный алгоритм с асимптотикой O(N^2)

Здесь уже чуточку интереснее. У нас имеется строка, и два временных массива для палиндромов чётной и нечётной длины. А число в ячейке i массива будет хранить количество палиндромов в строке s(исходная строка) с центром в точке i. Для нечётной длины палиндрома центр находится легко, ну а для чётной мы просто чуть поиграемся с индексами и сместим чуточку центр(что видно в коде). Наш результат это есть сумма чисел из двух массивов.

Как видите, снова ничего сложного. Но работает это заметно быстрее предыдущего алгоритма. Почему? Давайте рассмотрим, как же оно всё работает.

Мы бежим по строке, перебирая центральный символ нашего потенциального палиндрома. А потом просто бежим влево и вправо от центрального элемента до тех пор, пока символы одинаковы. Как только они стали разными, это значит, что дальше не будет палиндромов с центром в нашем выбранном элементе, и переходим к следующему.

А работает это быстро на обычных строках очень быстро потому, что наш второй, вложенный цикл, который бежит до тех пор, пока крайние символы равны, обрывается крайне быстро(если предположить, что палиндромов в строке много меньше общего числа подстрок).

Рассмотрим плюсы и минусы способа.

+ Всё также легко кодится. Ошибиться очень сложно.
+ Малая скрытая константа
+ Хорошо ведёт себя на случайных строках

— Всё ещё долгое время работы

После этого способа уже голова начинает думать-думать-думать. И тут идея! А что если мы модифицируем этот способ, только будем от центрального элемента прыгать не на 1 символ с каждой итерацией, а на чуточку больше? И тут нам на помощь приходят…

2) Используем хеши!

Этот способ чуточку сложнее, поэтому сразу приведу код, а потом постараюсь обьяснить, что за магия там творится(хотя магии нет, как вы сами прекрасно знаете):

Краткая суть данного способа: мы перебираем центральный элемент нашего палиндрома, и потом дихотомией стараемся найти наибольший радиус нашего палиндрома (под радиусом здесь понимается расстояние от центрального элемента до крайнего, если у нас палиндром чётной длины, то просто добавим чуточку игры с индексами, чтобы всё работало). Во время подбора мы должны как-то быстро сравнивать подстроки на идентичность. делаем это с помощью хешей. Асимптотика, как легко догадаться: N тратим на перебор центрального элемента, logN в худшем случае тратим на подбор радиуса палиндрома, за единицу сравниваем подстроки с помощью хешей. Итого имеем O(NlogN), что очень даже неплохо на самом деле.

Теперь чуть подробнее остановимся на данном методе.

На чём основывается наш метод? Так как мы перебираем центральный элемент, а потом дихотомией подбираем радиус наибольшего палиндрома с центром в данном элементе, то мы должны быстро брать хеш левой части нашего потенциального палиндрома и сравнивать его с хешем правой части нашего потенциального палиндрома.

Как это сделать? Давайте предварительно рассчитаем хеш для каждого префикса и суффикса исходной строки. В коде это у нас делают методы CountingPrefixHash() и CountingSuffixHash() соответственно.

С помощью методов getHash() и getRevHash() мы можем быстро получить хеши левой и правой частей рассматриваемого на данном этапе потенциального палиндрома. Тут может возникнуть вопрос, почему нельзя воспользоваться одной и той же функцией подсчёта хеша для левой и правой частей. А всё потому, что мы при проверке на палиндромность левую часть мы читаем слева направо, а вторую справа налево. И нам необходимо поддерживать хеш слева направо и справа налево.

Осталась единственная сложность: как сравнить этих 2 хеша? И эту проблему мы решаем с помощью метода isPalindrome(), который приводит хеши к одному основанию и сравнивает их.

Результатом каждой итерации у нас будет количество палиндромов с центром i. Пробегаемся 2 раза для палиндромов чётной и нечётной длины, ответ на нашу задачу есть сумма всех значений массивов oddCount и evenCount

Более подробно про данный метод вы можете почитать в этой статье.

+ Асимптотически мы снизили до NlogN, что не может не радовать. Если брать только худшие случаи, то в теории когда-нибудь мы выиграем

— Довольно тяжело пишется. Легко посеять багу. Нужна немного теоретическая подготовка в области хешей.
— Медленно работает на случайных тестах. Вы можете сами в этом убедиться. А всё из-за большой скрытой константы и из-за того, что даже если у нас нет ни одного палиндрома с центром в данном элементе, то алгоритм сделает logN прыжков, а это всё занимает время.
— Коллизии. Как вы видите, в моём исходнике используется хеш, который обычно пишут на олимпиадах по программированию(да-да, я немного этим когда-то занимался). Так вот, на соревнованиях данный способ показывает себя хорошо. Лично у меня коллизии не случались. Но я знаю про способы спокойно данный хеш завалить(в частности способ с использованием строк Туэ-Морса). Я когда-то слышал, что есть какой-то фиббоначиевый хеш, который вроде бы не ломается на данном тесте, но информация недостоверная. Так что будьте осторожны с коллизиями.

А если мы хотим 100% решение без всякой там коллизийной поправки и ввода хеша по другому основанию и так далее?

3) Алгоритм Манакера

Итак, мы получили с помощью хешей алгоритм за NlogN. Но хочется быстрее. Хочется чего-то линейного. И тут нам на помощь спешит Алгоритм Манакера (по ссылке вы также можете видеть реализацию алгоритма на Java), который мало того, что линеен, так ещё и обладает крайне малой скрытой константой, что положительно сказывается на его скорости работы. Подробно описывать способ я не буду, так как это получится пересказ этой замечательной ссылки (я сам учил алгоритм именно по этой ссылке). Здесь я приведу слегка пересказанное объяснение.

Алгоритм заключается в том, что мы обрабатываем строку символ за символом, поддерживая самый правый палиндром в нашей строке. И на каждой итерации смотрим, наш текущий элемент находится внутри границ самого правого палиндрома или нет. Если находится, то мы можем извлечь ответ из ранее посчитанных значений, путём нехитрых манипуляций с индексами. Если же не находится, то мы идём точно таким же алгоритмом, который описан в пункте 1) этого обзора: идём символ за символом и сравниваем зеркальные элементы относительно центра. Идём до тех пор, пока они равны. И не забываем обновить после этого границы самого правого найденного палиндрома. Это вкратце. Про некоторые подводные камни вы можете почитать в приведённой статье.

Что ещё интересного: во всех задачах, которые я решал на контестах (по олимпиадному программированию), хватало именно этого алгоритма. Очень просто пишется, если ты его писал N раз дома и уже знаешь наизусть.

+ Довольно короткий код.
+ Очень быстро работает. Мало того, что асимптотика O(N), так ещё и малая скрытая константа.

— Идея не такая простая, чтобы самому сходу придумать данный алгоритм
— Можно запутаться во всяких индексах, если проявить невнимательность при написании кода

А есть ли другие способы решить данную задачу за линейное время?

4) Дерево палиндромов

Немного предыстории. Эту относительно новую структуру данных открыл Михаил Рубинчик rumi13 и представил её на Петрозаводских сборах. Структура крайне интересная своей с одной стороны простотой, а с другой тем, что позволяет быстро решать довольно широкий спектр задачи про палиндромы. И самое главное — позволяет довольно просто считать количество палиндромов в строке за O(N) (но само дерево палиндромов думаю придумывалось далеко не для этого, а для более серьёзных задач с палиндромами).

Опять же, перескажу вкратце суть данного алгоритма. С более подробным разъяснением вы можете ознакомиться в этой замечательной статье.

Итак, идея дерева. В вершинах нашего дерева будут находиться только сами палиндромы: ‘a’, ‘b’, ‘aba’ и так далее. Понятно, что сам палиндромы мы не будем хранить, а просто будем хранить из какой вершины мы пришли сюда, и какой символ с двух сторон добавили. Также у нас существуют две фиктивные вершины для удобной реализации алгоритма.

Но как и в любом интересном дереве, у нас также существуют суффиксные ссылки. Суффиксная ссылка будет вести в вершину, которая также является палиндромом (ну потому что у нас в вершинах хранятся только палиндромы) и которая является наибольшим собственным суффиксом данной вершины. То есть из вершины ‘aba’ ссылка будет вести в вершину ‘a’.

Далее, мы по очереди добавляем символы в дерево по одному. И благодаря хитрому устройству дерева и рекурсивной операции добавления (а также суффиксным ссылкам, по которым осуществляется переход), мы обновляем всё дерево.

Это вкратце, подробнее почитайте информацию по ссылке выше (если не боитесь английского)

+ Если Вы ранее работали с деревьями, то вам будет очень просто понять данную идею.
+ Позволяет решать большой спектр задач на палиндромы

— Работает медленнее, чем алгоритм Манакера.
— Можно поставить багу. Но, чисто субъективно, тут это сделать сложнее, чем в том же алгоритме Манакера.

Также стоит упомянуть, что с помощью деревьев существует ещё одно решение данной задачи. Оно заключается в использовании суффиксного дерева и быстрого алгоритма LCA(который работает за препроцессинг O(N) и ответ на запрос O(1). Алгоритм Фарах-Колтон-Бендера). Но он на практике не применяется, так как довольно сложен и у него крайне большая скрытая константа. Представляет скорее академический интерес.

Что может быть ещё интересно про алгоритмы? Правильно, потребление памяти и время работы.
На гитхабе Вы можете скачать также код для тестирования, который генерирует случайные строки и ищет в них палиндромы.

Моё тестирование показало, что ожидаемо алгоритм номер 0 работает крайне медленно. Лидером, как Вы можете догадаться, является алгоритм Манакера. Но что самое интересное: алгоритм с O(N^2) выигрывает с примерно двукратным отрывом у алгоритма с использованием хешей с O(NlogN), что ещё раз доказывает, что не асимптотикой единой меряются алгоритмы. Так происходит из-за особенностей отсечения алгоритма номер 1, и отсутствия оной в способе с хешами. Что касается дерева палиндромов, то оно проигрывает Манакеру в основном из-за операций с памятью, так как приходится выделять память под каждую новую вершину. Но если использовать, например, new с размещением, то разрыв сократится.

Память все алгоритмы потребляют линейно от размера входных данных.

На этом мы завершим наш обзор. Надеюсь, что вы почерпнули для себя хоть что-то новое и вам было хоть чуточку интересно! Все исходники вы можете найти в моём публичном репозитории на Github.

P.S.: Если вы заметили какие-то опечатки, неточности или у вас есть дополнения — прошу отписываться в комментариях и писать в ЛС.
P.P.S.: Смело задавайте вопросы в комментариях — постараюсь ответить, если хватит моей компетенции.

Полезные ссылки, которые могут быть вам интересны после прочтения данной статьи (некоторые ссылки могут повторяться, так как могли проскакивать в самой статье):

0) Что такое палиндром
1) Алгоритм Манакера: Вики, Codeforces, e-maxx
2) Немного про хеши и их применение: e-maxx, Habrahabr
3) Обсуждение про завал хешей на Codeforces: тыц
4) Строки (слова) Туэ-Морса: раз, два
5) Статьи про дерево палиндромов: хорошее описание, codeforces
6) Вот ещё цикл статей про поиск чисел-палиндромов: Хабр

Источник

• ← Машина тьюринга принцип работы кратко
• Машина тьюринга простым языком →