Машина тьюринга увеличить двоичное число на 1
Машина Тьюринга на формулах Excel
Что такое Машина Тьюринга
Простой пример: прибавление единицы к двоичному числу
Для такой машины потребуется алфавит из трех символов (0,1, х) – где 0 и 1 будут для числа, а х для пустой ячейки. То есть пустая лента вся заполнена символами «х».
У головки будет 4 состояния: q1,q2,q3 и q4 – остановка машины.
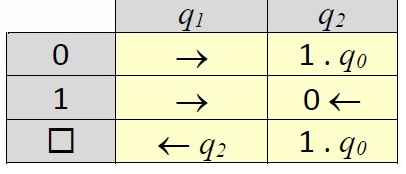
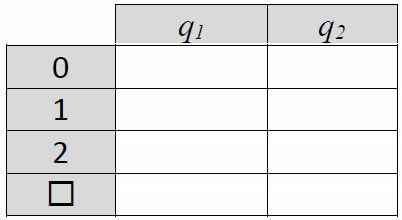
Правила для машины выпишем в виде матрицы: 
Нетрудно проверить, что такая машина при помещении головки на старший разряд двоичного числа, при начальном состоянии q1, увеличит это число на 1.
Реализация на Excel
Создадим таблицу правил, как в примере выше. Выделим всю эту таблицу и назовем ее «rules». Жмем Enter.
Зададим начальное состояние ленты:
Оно означает, что на ленте записано число 10111, а головка находится в состоянии 1, и в ячейке, соответствующей старшему разряду. Excel поддерживает условное форматирование, что и применено для большей наглядности.
Новый шаг машины будет моделироваться новыми строками эксель, а формулы будут имитировать состояние машины согласно правилам.
Формула для ячейки ленты:
=ЕСЛИ(K14<>0; ИНДЕКС(rules;K14+1;2+K13*3);K13)
Эта формула для значения ячейки ленты на следующем шаге (K17). Она означает, что если головка (K14) находится под ячейкой (то есть в клетке K14 не ноль), то следует записать в эту ячейку значение согласно правилам (из массива rules). Если же в клетке под ячейкой ленты ноль (что значит, под ней нет головки), то значение не меняется.
Формула для состояния головки (для удобства чтения сделаны переносы строки):
=ЕСЛИ(K14<>0; ЕСЛИ(ИНДЕКС(rules;K14+1;4+K13*3)=0; ИНДЕКС(rules;K14+1;3+K13*3);0);
ЕСЛИ(J14<>0; ЕСЛИ(ИНДЕКС(rules;J14+1;4+J13*3)=1; ИНДЕКС(rules;J14+1;3+J13*3);0);
ЕСЛИ(L14<>0; ЕСЛИ(ИНДЕКС(rules;L14+1;4+L13*3)=-1; ИНДЕКС(rules;L14+1;3+L13*3);0);0)))
Эта формула
1) сначала проверяет, находится ли головка в этой ячейке (K14) – тогда если правила говорят оставаться на месте, в эту клетку пишется состояние машины согласно правилам
2) Если головка находится на одну ячейку влево (J14) и правила говорят сдвинуться вправо – тогда в эту клетку пишется состояние машины согласно правилам
3) Если головка находится на одну ячейку справа (L14) и правила говорят сдвинуться влево – тогда в эту клетку пишется состояние машины согласно правилам
4) Во всех остальных случаях пишется ноль
Такая формула имитирует движение головки.
В формулах использована функция Индекс(массив, строка, столбец). Вычислим значение ИНДЕКС(rules;K14+1;4+K13*3) – кусочка формулы состояния головки.
Как видно из рисунка, K14=1, K13=1. Значит надо найти ИНДЕКС(rules;1+1;4+1*3) то есть ИНДЕКС(rules;2;7) – значение в массиве «rules» на пересечении 2й строки и 7го столбцы (нумеруются строки и столбцы начиная с 1, а не 0). В нашей табличке это значение «1».
Формулы относительные – то есть при копировании их на новые ячейки эксель берет данные из ячеек соответствующий предыдущему состоянию машины.
В итоге, выполнив все шаги, машина «останавливается» — достигнуто состояние «4», к числу прибавлена единица.
Вот ссылка на файл Excel
Заключение
Если бы Эксель поддерживал сколь угодно большое число строк и столбцов, то это автоматически означало бы, что используя формулы экселя можно реализовать любую вычислимую функцию, так как Excel был бы Тьюринг-полным
Машина тьюринга увеличить двоичное число на 1
Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным. Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A=
Q=
Каждая ячейка ленты может содержать символ из внешнего алфавита A =
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q =
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), «
Машина Тьюринга
Первым из всех ученых идею универсального исполнителя предложил Алан Тьюринг (1936г.). Для уточнения понятия алгоритма, им был разработан абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Машина Тьюринга состоит из:
— бесконечной в обе стороны ленты, разделенной на ячейки;
— каретки (читающей и записывающей головки);
Программируемый автомат управляет кареткой, посылая ей команды в соответствии с заложенной в него сменяемой программой. Лента выполняет роль внешней памяти компьютера, автомат — роль процессора, а каретка служит для ввода и вывода данных.
Программа для машины Тьюринга
Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
Внешний алфавит. Конечное множество (обозначают буквой А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.
Например, алфавит машины Тьюринга, работающей с двоичными числами, задается в виде A = <0, 1, а0>.
Непрерывную цепочку символов на ленте называют словом.
Автоматом называют устройство, работающее без участия человека. Автомат в машине Тьюринга имеет несколько состояний и при определенных условиях переходит из одного состояния в другое. Множество состояний автомата называют внутренним алфавитом.
Таблица переходов. Описание поведения автомата (каретки) в зависимости от состояния и считанного символа.
Автомат машины Тьюринга в процессе своей работы управляется программой, во время каждого шага которой выполняются последовательно следующие действия:
— Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
— Передвигаться на одну ячейку влево или вправо.
— Менять свое внутреннее состояние.
Поэтому при составлении программы для каждой пары (символ, состояние) нужно определить три параметра: символ ai из выбранного алфавита A, направление перемещения каретки («←” — влево, «→” — вправо, «точка” — нет перемещения) и новое состояние автомата qk.
Например, команда 1 «←” q2 обозначает «заменить символ на 1, переместить каретку влево на одну ячейку и перейти в состояние q2”.
Предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.
Примеры работы машины Тьюринга
На ленте записано число в двоичной системе счисления. Каретка находится где-то над числом. Требуется увеличить число на единицу.
Чтобы решить задачу, нам нужно:
-определить алфавит машины Тьюринга А,
— определить набор состояний Q,
— составить программу (т.е. для каждой пары (аi,qi) определить команду автомата.)
Алфавит машины Тьюринга, работающей с двоичными цифрами будет включать цифры 0, 1 и пробел a0. Т.е. А=<1,0,a0>.
Определим возможные состояния:
3) если в рабочей ячейке пробел, переместить каретку влево и перейти в состояние q2
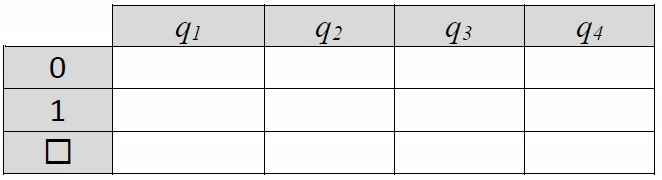
Составим таблицу переходов для q1 т.о.:
1) если в рабочей ячейке записана цифра 0, записать в нее 1 и стоп
2) если в рабочей ячейке записана цифра 1, выполнить перенос в старший разряд — записать в ячейку 0 и переместиться влево.
3) если в рабочей ячейке пробел, записать в нее 1 и стоп.
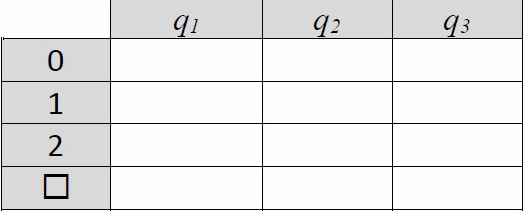
Добавим в нашу таблицу состояние q2:
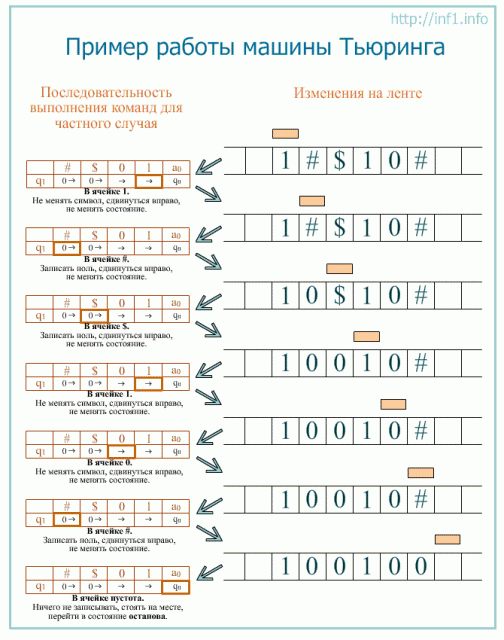
Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость).
Вопросы: 1
1. Что такое универсальный исполнитель?
2. Опишите устройство и систему программирования машины Тьюринга.
3. Что такое состояние машины Тьюринга?
4. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера?
5. В чем особенность состояний q0 и q1 машины Тьюринга?
6. По какому принципу можно построить программу для машины Тьюринга, которая последовательно выполняет операции А и Б?
7. Сформулируйте тезис Чёрча — Тьюринга.
Компьютерный практикум:
(Методические материалы И.Г. Семакина. Сетевой семинар «Преподавание профильного курса информатики»)
1. Дано целое число в троичной системе счисления; нужно увеличить его на единицу. Для реализации программы использовать учебную модель машины Тьюринга.
2. К данному троичному числу прибавить 2.
3. Прибавление единицы для целых чисел в пятеричной системе счисления
4. Составьте два варианта программы для машины Тьюринга, решающей следующую задачу: целое десятичное число нужно умножить на 10. Головка автомата расположена: а) левее числа на какой-то свободной ячейке; б) правее числа на какой-то свободной ячейке.
5. На ленте машины Тьюринга слева от головки автомата расположена группа подряд стоящих звездочек. Нужно стереть все звездочки и получить на ленте число, равное первоначальному количеству звездочек. Составить программу, реализовать ее на учебной модели машины Тьюринга. Протестировать программу.
Машина Тьюринга программа (К. Поляков)
Дополнительный материал:
1. Тренажер для изучения работы машины: программа (К. Поляков) (пароль к архиву kpolyakov.narod.ru)
4. Пильщиков В.Н., Абрамов В.Г., Вылиток А.А., Горячая И.В. Машины Тьюринга и алгоритмы Маркова. Решение задач. М.: МГУ, 2006.
1. К.Ю. Поляков, Е.А. Еремин «Элементы теории алгоритмов». Журнал «Информатика» №1, 2012 г.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Уточнение понятия алгоритма. ГДЗ по Информатике 11 класс.
Информатика. 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю., Еремин Е.А.
§ 34. Уточнение понятия алгоритма
Вопросы и задания
1. Зачем понадобилось уточнять понятие «алгоритм»?
2. Какие задачи рассматриваются в теории алгоритмов?
3. Почему можно ограничиться алгоритмами обработки символьных строк? Можно ли рассматривать только алгоритмы для преобразования двоичных кодов?
4. Как вы понимаете утверждение «Алгоритм задаёт некоторую функцию»?
5. Как связаны понятия «алгоритм» и «исполнитель»?
6. Что такое программа?
7. В каком случае говорят, что два алгоритма эквивалентны?
8. Что такое универсальный исполнитель?
9. Сравните интуитивное и строгое понятия алгоритма.
10. Опишите устройство и систему программирования машины Тьюринга.
11. Что такое состояние машины Тьюринга?
12. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера?
13. В чем особенность состояний q0 и q1, машины Тьюринга?
14. По какому принципу можно построить программу для машины Тьюринга, которая последовательно выполняет операции А и Б?
15. Сформулируйте тезис Чёрча-Тьюринга.
16. Сравните машины Тьюринга и Поста.
17. Зачем нумеруются строки в программе для машины Поста?
18. Что такое нормальный алгорифм Маркова?
19. Зачем используют специальные символы в НАМ?
20. Что означает эквивалентность различных универсальных исполнителей?
Подготовьте сообщение
а) «Какие бывают машины Тьюринга?»
б) «Эзотерические языки программирования»
в) «Рекурсивные функции»
Задача
1. Что делают следующие программы для машины Тьюринга?
В каких случаях эти программы зацикливаются?
2. Предложите программу для машины Тьюринга и начальное состояние ленты, при котором эта программа зацикливается.
3. Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1.
4. Составьте программы для машины Тьюринга, которые увеличивают и уменьшают на единицу число, записанное в десятичной системе счисления.
5. Составьте программу для машины Тьюринга, которая складывает два числа в двоичной системе, разделенные на ленте знаком «+».
6. Составьте программы для машины Тьюринга, которые выполняют сложение и вычитание двух чисел в десятичной системе счисления.
7. Что делают следующие программы для машины Поста?
Как будет работать каждая из программ при различных начальных состояниях ленты?
8. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
9. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
10. Что делают следующие НАМ, если применить их к символьной цепочке, состоящей из нулей и единиц?
Как будет работать каждая из программ при различных начальных состояниях ленты?
11. Напишите НАМ, который сортирует цифры двоичного числа так, чтобы сначала стояли все нули, а потом — все единицы.
12. Напишите: НАМ, который удаляет поглгдпий символ строки, состоящей из цифр 0 и 1. Какую операцию он выполняет, если рассматривать строку как двоичную запись числа.
13. Напишите НАМ, который умножает двоичное число на 2, добавляя О в конец записи числа.
Практическая работа № 36
«Машина Тьюринга»
Файлы-заготовки для выполнения этой практической работы
Файлы-заготовки для выполнения этой практической работы 1. Наберите программу из учебника (или из презентации), которая увеличивает двоичное число на 1 и проверьте её работу.
Будет ли правильно работать эта программа, если вначале каретка расположена справа от числа? Почему?
2. Измените программу для увеличения двоичного числа на 1 так, чтобы она работала правильно, если вначале каретка расположена справа от числа.
3. Опишите алгоритм работы программы для машины Тьюринга:
При каком начальном состоянии ленты и положении каретки эта программа зацикливается?
4. Составьте программу для машины Тьюринга, которая заменяет в двоичном числе все 0 на 1 и все 1 на 0 (из числа 10101100 получается 01010011). Каретка находится слева от числа.
5. Составьте программу для машины Тьюринга, которая умножает двоичное число на 2. Каретка находится над числом.
6. Составьте программу для машины Тьюринга, которая увеличивает троичное число на 1. Каретка находится справа от числа.
При каком начальном положении каретки эта программа зацикливается?
7. Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1. Каретка находится над числом.
При каком начальном положении каретки эта программа зацикливается?
8. Составьте программу для машины Тьюринга, которая умножает троичное число на 2. Каретка находится над числом.
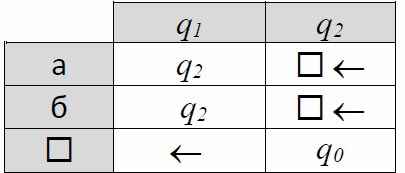
9. Дана строка, состоящая только из символов «а» и «б». Составьте программу для машины Тьюринга, которая переставляет последний символ в начало строки. Каретка находится над первым символом строки.
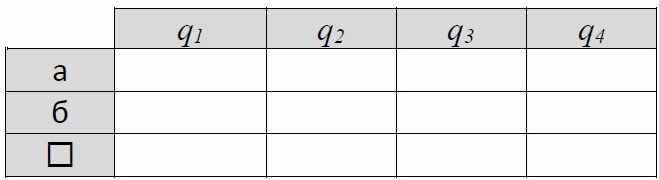
10. *Дана строка, состоящая только из символов «а» и «б». Составьте программу для машины Тьюринга, которая сортирует символы, то есть переставляет все буквы «а» в начало строки. Каретка находится над первым символом строки. Используйте состояния, которые перечислены род таблицей.
11. *Составьте программу для машины Тьюринга, которая складывает два числа в двоичной системе, разделенные на ленте знаком «+».
12. *Составьте программы для машины Тьюринга, которые увеличивают и уменьшают на единицу число, записанное в десятичной системе счисления.
13. Составьте программы для машины Тьюринга, которые выполняют сложение и вычитание двух чисел в десятичной системе счисления.