Начальная координата автомобиля 300 м а велосипедиста 100
1385. Верно ли выражение: в телескоп мы видим предметы в «увеличенном виде»?
Мы видим увеличенные изображения предметов.
1386. Какая из двух луп дает большее увеличение: с фокусным расстоянием 4 см или 2 см?
1387. Фокусное расстояние человеческого глаза около 15 мм. Вычислите его оптическую силу.
1388. Изображение диапозитива размером 8,5 ͯ 8,5 см желают получить на экране, имеющем размеры 1,5 м ͯ 2 м, находящемся на расстоянии f = 6 м от проекционного аппарата. Какое фокусное расстояние должен иметь для этой цели объектив?
1389. Какое увеличение дает лупа в 10 диоптрий?
1390. Фокусное расстояние объектива микроскопа 4 мм, а окуляра 2,5 см. Определите увеличение этого микроскопа, если предмет помещается на 0,2 мм дальше фокуса объектива.
1391. Объектив телескопа имеет фокусное расстояние 10 м, а окуляр 5 см. Определите увеличение, даваемое этим телескопом.
1392. Отличается ли хрусталик здорового глаза от хрусталика близорукого глаза? дальнозоркого глаза? Если да, то в чем состоит отличие?
Отличается. Здоровый хрусталик фокусирует изображение точно на сетчатке. При дальнозоркости фокус располагается за сетчаткой. При близорукости фокус располагается перед сетчаткой.
1393. Какие линзы применяются при близорукости?
Рассеивающие линзы.
1394. Какие линзы применяются при дальнозоркости?
Собирающие линзы.
1395. Можно ли считать автомобиль материальной точкой при определении пути, который он проехал за 2 ч? за 2 с?
В первом случае можно. Во втором случае нельзя, потому что тело можно считать материальной точкой тогда, когда его размеры меньше расстояний, рассматриваемых в задаче.
1396. Можно ли рассматривать поезд длиной 200 м как материальную точку при определении времени, за которое он проехал расстояние 2 м?
Нельзя. Длина поезда больше пройденного им расстояния. Для рассмотрения поезда в качестве материальной точки расстояние, пройденное им, должно быть больше его собственной длины.
1397. Можно ли считать поезд длиной 200 м материальной точкой при определении времени, за которое он проехал мост длиной 800 м?
Можно.
1398. Муха ползет по краю блюдца из точки А в точку В (рис. 176). На рисунке покажите:
а) траекторию движения мухи;
б) перемещение мухи.
1399. При каком движении материальной точки путь, пройденный точкой, равен модулю перемещения?
При прямолинейном.
1400. Рота солдат прошла на север 4 км, затем солдаты повернули на восток и прошли еще 3 км. Найдите путь и перемещение солдат за все время движения. Нарисуйте в тетради траекторию их движения.
1401. Найдите координаты точек А, В и С в системе координат XOY (рис. 177). Определите расстояния между точками:
а) А и В, б) В и С, в) А и С.
1402. На рисунке 178 показаны перемещения трех материальных точек: s1, s2, s3. Найдите:
а) координаты начального положения каждой точки;
б) координаты конечного положения каждой точки;
в) проекции перемещения каждой точки на координатную ось OX;
г) проекции перемещения каждой точки на координатную ось OY;
д) модуль перемещения каждой точки.
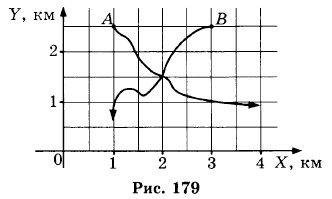
1404. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
1406. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось OX, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату x0 начального положения мяча;
б) координату xm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1407. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.
Материальная точка. Система отсчета. Перемещение. Определение координаты
Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.
1404. Можно ли считать автомобиль материальной точкой при определении пути, который он проехал за 2 ч? за 2 с?
В первом случае можно. Во втором случае нельзя, потому что тело можно считать материальной точкой тогда, когда его размеры меньше расстояний, рассматриваемых в задаче.
1405. Можно ли рассматривать поезд длиной 200 м как материальную точку при определении времени, за которое он проехал расстояние 2 м?
Нельзя. Длина поезда больше пройденного им расстояния. Для рассмотрения поезда в качестве материальной точки расстояние, пройденное им, должно быть больше его собственной длины.
1406. Можно ли считать поезд длиной 200 м материальной точкой при определении времени, за которое он проехал мост длиной 800 м?
Можно.
1407. Муха ползет по краю блюдца из точки А в точку В (рис. 176). На рисунке покажите:
а) траекторию движения мухи;
б) перемещение мухи.
1408. При каком движении материальной точки путь, пройденный точкой, равен модулю перемещения?
При прямолинейном.
1409. Рота солдат прошла на север 4 км, затем солдаты повернули на восток и прошли еще 3 км. Найдите путь и перемещение солдат за все время движения. Нарисуйте в тетради траекторию их движения.
1410. Найдите координаты точек А, В и С в системе координат XOY (рис. 177). Определите расстояния между точками:
а) А и В, б) В и С, в) А и С.
1411. На рисунке 178 показаны перемещения трех материальных точек: s1, s2, s3. Найдите:
а) координаты начального положения каждой точки;
б) координаты конечного положения каждой точки;
в) проекции перемещения каждой точки на координатную ось OX;
г) проекции перемещения каждой точки на координатную ось OY;
д) модуль перемещения каждой точки.
1413. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
1415. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось OX, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату x0 начального положения мяча;
б) координату xm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1416. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.
Начальная координата автомобиля 300 м а велосипедиста 100
На рисунке представлен график зависимости пути S велосипедиста от времени t.
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
На других интервалах скорость была иная.
Правильный ответ указан под номером 4.
а на интервале от 10 до 30, он же тоже двигается 5 м/с
На этом интервале пройденный им путь не изменяется, а значит, он покоится.
Тоесть,он двигается со скоростью 5м/c,но пройденный путь не изменяется?
Нет, раз его путь не изменяется, значит его скорость на этом интервале времени равна нулю.
А в интервале времени от 50 до 70 сек,разве скорость равнялась не 5м/c? 100м/20c=5(м/c)
В интервале от 50 до 70 с скорость велосипедиста равнялась
На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
Пункт A находится в точке а пункт Б — в точке
Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна
Здесь использована формула для движения без ускорения. Но если всмотреться в график, то можно заметить, что за первые 0,1ч автобус прошел 5км. За вторые 0,1 км автобус проехал уже больше 5км.
То есть движение-то получается не равномерное.
Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки: Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение:
что в этой задаче является
1. скоростью относительно неподвижной с.о.
2. скоростью относительно подвижной с.о.
3. переносной скоростью
1. скорость относительно неподвижной с.о. — скорость пловца относительно берега ;
2. скорость относительно подвижной с.о. — скорость пловца относительно воды ;
3. переносная скорость — скорость воды относительно берега .
Если бы он бы плыл против течения, то ответ был бы 0,1 м/с?
Все верно, но была бы она направлена в противоположную сторону.
Ваше решение совершенно верно. Однако есть некоторая небрежность в определении переносной скорости.
Переносной скоростью нельзя называть скорость движения системы отсчета, тем более при вращательном движении СО понятие скорости СО вообще исчезает, так как разные ее точки имеют разные скорости.
Итак, Vа=Vп+Vо (в формулах все величины векторные). С определением абсолютной и относительной скорости нет проблем. Так что же такое переносная скорость? Определение легко дать, исходя из самой формулы. Если Vо=0, то Vа=Vп. То есть переносная скорость это скорость точки в неподвижной системе, если в подвижной системе она покоится. Это скорость, с которой подвижная система переносит относительно неподвижной покоящуюся на ней точку. Потому она и называется переносной.
Из такого понятия и вытекает, что в нашем случая скорость течения реки и есть переносная скорость.
Спасибо за уточняющий комментарий.
Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: То есть, буквально, надо весь пройденный телом путь разделить на всё время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберёмся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через L, тогда весь путь, пройденный велосипедистом, равен На первую половину пути велосипедист затратил время
На обратную дорогу — время
Всё время пути составило
Окончательно, находим, что средняя путевая скорость велосипедиста равна
Начальная координата автомобиля 300 м а велосипедиста 100
По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)
Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале времени от 0 до 2 с автомобиль прошёл путь
Примечание. В принципе, интересующий нас участок (от 0 до 2 с) не обязательно разбивать на два, площадь под графиком можно посчитать, как площадь трапеции:
В принципе, можно использовать стандартные кинематические формулы для изменения координаты, скорости, ускорения, а все необходимые данные снимать с графика. Но так получается значительно дольше.
Почему же не через площадь дольше?
S= So + vt + (at^2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;
Правильно. Так тоже можно.
В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.
В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂
Утверждение «в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)» не совсем верно, правильно тогда уж говорить так: «за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с».
Однако такое утверждение в свою очередь требует разъяснений.
так путь же нужно найти почему нельзя воспользоваться формулой S=Vt
Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется
В задании не сказано, но тело двигалось прямолинейно
Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.
На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)
Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь
Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.
Материальная точка. Система отсчета. Перемещение. Определение координаты движущегося тела
1394. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?
а) модуль перемещения автомобиля;
б) модуль перемещения велосипедиста;
в) проекцию перемещения каждого тела на ось ОХ;
г) путь, пройденный каждым телом;
д) расстояние между телами в начальный момент времени;
е) расстояние между телами в конечный момент времени.
1396. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось ОХ, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату х0 начального положения мяча;
б) координату хm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.
1397. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.