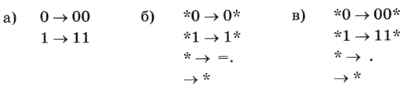Напишите программу для машины поста которая складывает два числа в единичной системе счисления
Напишите программу для машины поста которая складывает два числа в единичной системе счисления
МАШИНЫ ПОСТА И ТЬЮРИНГА
Машина Поста состоит из ленты, разбитой на ячейки, и каретки, которая может считывать содержимое обозреваемой ячейки, стирать метки и ставить метки. Создайте компьютерную модель машины Поста, вычитающей два числа.
Алгоритм вычитания целых чисел для машины Поста приведен ниже. В первых двух строчках указывается положение каретки и состояние ленты, на которой в унарной системе счисления записаны два числа (в данном случае 6 и 4). В результате исполнения программы на ленте останется число 2 в унарной системе счисления.
Рис. 1. Вычитание целых чисел.
Напишите компьютерную программу, моделирующую машину Поста, которая увеличивает целое число на 2.
Алгоритм увеличения целого числа на 2 представлен ниже:
Для реализации этого алгоритма в процедуру Programma программы ПР-1 необходимо вставить следующий код:
Рис. 2. Увеличение числа на 2
Напишите компьютерную программу, моделирующую машину Поста, которая уменьшает целое число на 2.
Пусть на ленте машины Поста записано число 6, каретка находится напротив левой ячейки (координата x=1). Для вычитания из любого целого N числа 2 в процедуру Programma программы ПР-1 следует вставить следующий код:
Рис. 3. Уменьшение целого числа на 2
Напишите компьютерную программу, моделирующую машину Поста, которая складывает два целых числа.
Программа сложения целых чисел на машине Поста выглядит так:
В программу ПР-1 следует вставить код:
Рис. 4. Сложение двух целых чисел
Напишите компьютерную программу, моделирующую машину Поста, которая умножает целое число на 2.
Результат решения представлен на рис. 5. Возможен другой способ решения:
Рис. 5. Умножение целого числа на 2
Машина Тьюринга состоит из бесконечной ленты и головки, которая перемещается относительно ленты, стирает символы, ставит новые символы. Напишите программу, моделирующую работу машины Тьюринга, которая увеличивает заданное число на 2.
Используется программа ПР-2. Состояние ленты машины Тьюринга записывается в массиве:
Программа для машины Тьюринга записывается в виде последовательности команд, представленных в общепринятом формате:
Программа для машины Тьюринга, увеличивающая целое число на 2, состоит из 3 команд:
Рис. 6. Увеличение целого числа на 2
Напишите программу для МТ, складывающую два целых числа, заданных набором единиц.
| q | «1» | «_» |
| 1 | 2_R | |
| 2 | 21R | 31R |
| 3 | 31R | 4_L |
| 4 | 1_S |
В программу ПР-2 следует вставить код:
Результат работы программы представлен на рис. 7.
Рис. 7. Сложение целых чисел
Пусть машина Тьюринга находится в состоянии 1. В компьютерную программу ПР-2 необходимо вставить следующий код:
Рис. 8. Замена единиц на звездочки и пробелы
Программа для машины Тьюринга имеет вид:
| q | «_» | «1» | «*» |
| 1 | 1_R | 3*R | |
| 2 | 2_L | 2*R | 3*L |
| 3 | 3_S | 2*R | 3*L |
Для решения этой задачи в программу ПР-2 следует вставить код:
Результат работы программы представлен на рис.9.
Рис. 9. Замена единиц на звездочки
Программа для машины Тьюринга выглядит так:
| q | «_» | «A» | «B» | «*» | » | « |
| 1 | 1_R | 2*R | 1BR | 1*R | 1|S |
| 2 | 3|R | 2AR | 2BR | 2*R | 3|R |
| 3 | 4AL | 3AR | |||
| 4 | 1_R | 4AL | 4BL | 4*L | 4|L |
В компьютерную программу ПР-2 следует вставить код:
Рис. 10. Группировка символов A
Программа для машины Тьюринга представлена в таблице:
| q | «_» | «1» | «2» | «3» | «4» | «5» | «6» | «7» | «8» | «9» | «0» |
| 1 | 2_L | 11R | 12R | 13R | 14R | 15R | 16R | 17R | 18R | 19R | 10R |
| 2 | 21S | 22S | 23S | 24S | 25S | 26S | 27S | 28S | 29S | 20L | 21S |
В программу ПР-2 следует вставить код:
Рис. 11. Увеличение числа на 1.
Тексты программ находятся в zip-архиве, файл gl-14.pas.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Уточнение понятия алгоритма. ГДЗ по Информатике 11 класс.
Информатика. 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю., Еремин Е.А.
§ 34. Уточнение понятия алгоритма
Вопросы и задания
1. Зачем понадобилось уточнять понятие «алгоритм»?
2. Какие задачи рассматриваются в теории алгоритмов?
3. Почему можно ограничиться алгоритмами обработки символьных строк? Можно ли рассматривать только алгоритмы для преобразования двоичных кодов?
4. Как вы понимаете утверждение «Алгоритм задаёт некоторую функцию»?
5. Как связаны понятия «алгоритм» и «исполнитель»?
6. Что такое программа?
7. В каком случае говорят, что два алгоритма эквивалентны?
8. Что такое универсальный исполнитель?
9. Сравните интуитивное и строгое понятия алгоритма.
10. Опишите устройство и систему программирования машины Тьюринга.
11. Что такое состояние машины Тьюринга?
12. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера?
13. В чем особенность состояний q0 и q1, машины Тьюринга?
14. По какому принципу можно построить программу для машины Тьюринга, которая последовательно выполняет операции А и Б?
15. Сформулируйте тезис Чёрча-Тьюринга.
16. Сравните машины Тьюринга и Поста.
17. Зачем нумеруются строки в программе для машины Поста?
18. Что такое нормальный алгорифм Маркова?
19. Зачем используют специальные символы в НАМ?
20. Что означает эквивалентность различных универсальных исполнителей?
Подготовьте сообщение
а) «Какие бывают машины Тьюринга?»
б) «Эзотерические языки программирования»
в) «Рекурсивные функции»
Задача
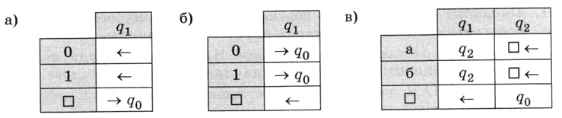
1. Что делают следующие программы для машины Тьюринга?
В каких случаях эти программы зацикливаются?
2. Предложите программу для машины Тьюринга и начальное состояние ленты, при котором эта программа зацикливается.
3. Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1.
4. Составьте программы для машины Тьюринга, которые увеличивают и уменьшают на единицу число, записанное в десятичной системе счисления.
5. Составьте программу для машины Тьюринга, которая складывает два числа в двоичной системе, разделенные на ленте знаком «+».
6. Составьте программы для машины Тьюринга, которые выполняют сложение и вычитание двух чисел в десятичной системе счисления.
7. Что делают следующие программы для машины Поста?
Как будет работать каждая из программ при различных начальных состояниях ленты?
8. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
9. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
10. Что делают следующие НАМ, если применить их к символьной цепочке, состоящей из нулей и единиц?
Как будет работать каждая из программ при различных начальных состояниях ленты?
11. Напишите НАМ, который сортирует цифры двоичного числа так, чтобы сначала стояли все нули, а потом — все единицы.
12. Напишите: НАМ, который удаляет поглгдпий символ строки, состоящей из цифр 0 и 1. Какую операцию он выполняет, если рассматривать строку как двоичную запись числа.
13. Напишите НАМ, который умножает двоичное число на 2, добавляя О в конец записи числа.
Машина Поста (устройство, команды и принцип работы)
Содержимое разработки

Машина Поста – это абстрактная (несуществующая реально) вычислительная машина, созданная для уточнения (формализации) понятия алгоритма. Представляет собой универсальный исполнитель, позволяющий вводить начальные данные и читать результат выполнения программы.
В 1936 г. американский математик Эмиль Пост в статье описал систему, обладающую алгоритмической простотой и способную определять, является ли та или иная задача алгоритмически разрешимой. Если задача имеет алгоритмическое решение, то она представима в форме команд для машины Поста.
Структура машины Поста:
Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (также как у машины Тьюринга). Каждая ячейка ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит.
Т.о., Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.
Алгоритм работы машины Поста задается не в виде таблицы, а как программа для универсального исполнителя.
Программа состоит из конечного числа строк и использует всего 6 команд.
где N. — номер строки, J — строка на которую переходит управление далее.
Попытка стереть метку там, где ее нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается.
Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки).
После запуска возможны варианты:
— работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
— работа может закончиться командой Stop;
— работа никогда не закончится.
Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n0,n1). С помощью этой команды можно также строить циклы, как с предусловием, так и с постусловием.
Пост предположил, что любой алгоритм может быть записан как программа для машины Поста.
В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.
После команд «←”, «→”, «0” и «1” можно указать номер строки, на которую нужно перейти сразу после выполнения этой команды. Например, команда ← 3 означает «переместить каретку влево и перейти на строку 3”.
При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счетные палочки в младшей школе).
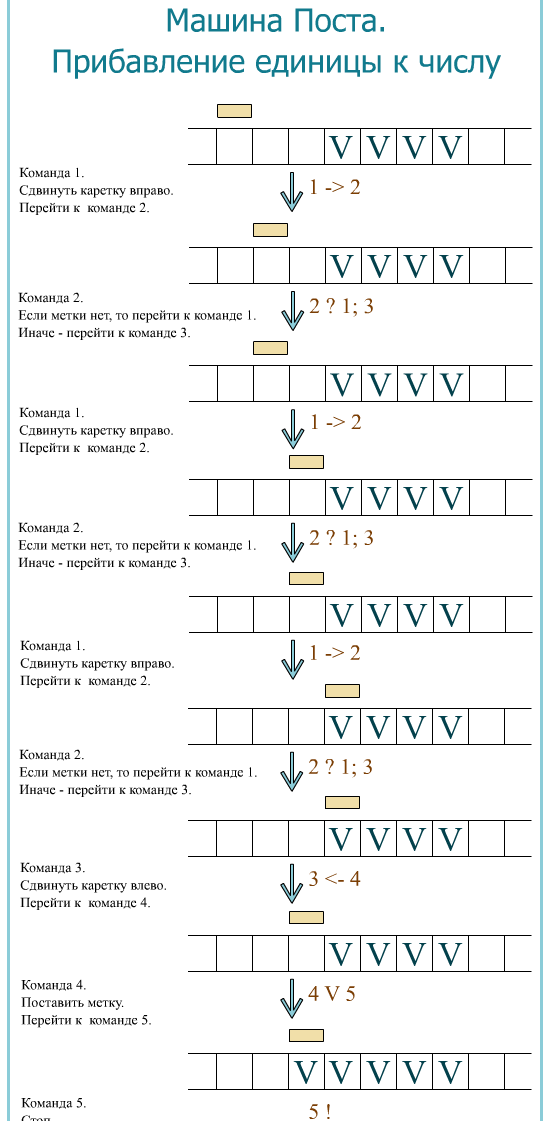
1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
2. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
Пример работы машины Поста:
Задача: увеличить число 3 на единицу (изменить значение в памяти с 3 на 4).
Целое положительное число на ленте машины Поста представимо идущими подряд метками, которых на одну больше, чем кодируемое число. Это связано с тем, что одна метка обозначает ноль, а уже две – единицу, и т.д.
Допустим, точно известно, что каретка стоит где-то слева от меток и обозревает пустую ячейку. Тогда программа увеличения числа на единицу может выглядеть так:
Машина Поста

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (также как у машины Тьюринга). Каждая ячейка ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит.
Т.о., Пост сократил алфавит всего до двух цифр. Это допустимо, потому что любые данные можно перекодировать в двоичный код, сопоставив каждой букве исходного алфавита уникальную последовательность нулей и единиц.
Алгоритм работы машины Поста задается не в виде таблицы, а как программа для универсального исполнителя.

где N. — номер строки, J — строка на которую переходит управление далее.
Попытка стереть метку там, где ее нет, или поставить метку повторно считается ошибкой, и машина аварийно останавливается
Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки).
После запуска возможны варианты:
— работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
— работа может закончиться командой Stop;
— работа никогда не закончится.
Все строки в программе нумеруются по порядку, это необходимо для работы команды ветвления (? n0,n1). С помощью этой команды можно также
строить циклы, как с предусловием, так и с постусловием.
После команд «←”, «→”, «0” и «1” можно указать номер строки, на которую нужно перейти сразу после выполнения этой команды. Например, команда ← 3 означает «переместить каретку влево и перейти на строку 3”.
При работе с машиной Поста числа обычно записывают в унарной (единичной) системе счисления, в виде непрерывной цепочки меток нужной длины (вспомните счетные палочки в младшей школе).
Пример работы машины Поста : прибавление к числу единицы.
Пост предположил, что любой алгоритм может быть записан как программа для машины Поста.
В теории алгоритмов доказано, что машины Поста и Тьюринга одинаковы по своим возможностям. Это значит, что круг задач, который они решают, тоже одинаков.
_________________________________________________________________________________________________
Вопросы:
1. Сравните машины Тьюринга и Поста.
2. Зачем нумеруются строки в программе для машины Поста?

1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
2. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
Как будет работать каждая из программ при различных начальных состояниях ленты?

(Методические материалы И.Г. Семакина)
1. На информационной ленте либо справа, либо слева от головки, стоящей под пустой клеткой, находится массив меток. Требуется присоединить к этому массиву одну метку. Составить универсальную программу. Реализуйте программу на учебной модели машины Поста. Протестируйте программу.
2. На ленте расположен массив из 2n-1 меток. Составить программу отыскания средней метки и стирания ее. Реализуйте программу на учебной модели машины Поста. Протестируйте программу.
3. На ленте расположен массив из 2n меток. Составить программу, по которой машина раздвинет на расстояние в одну клетку две половины данного массива. Реализуйте программу на учебной модели машины Поста. Протестируйте программу.
Машина Поста программа (К.Поляков)

1. К.Ю. Поляков, Е.А. Еремин «Элементы теории алгоритмов». Журнал «Информатика» №1, 2012 г.
Урок 33
Уточнение понятие алгоритма. Универсальные исполнители
§34. Уточнение понятия алгоритма
Содержание урока
Задачи
Задачи
1. Что делают следующие программы для машины Тьюринга?
В каких случаях эти программы зацикливаются?
2. Предложите программу для машины Тьюринга и начальное состояние ленты, при котором эта программа зацикливается.
3. Составьте программу для машины Тьюринга, которая уменьшает двоичное число на 1.
4. Составьте программы для машины Тьюринга, которые увеличивают и уменьшают на единицу число, записанное в десятичной системе счисления.
5. Составьте программу для машины Тьюринга, которая складывает два числа в двоичной системе, разделенные на ленте знаком «+».
6. Составьте программы для машины Тьюринга, которые выполняют сложение и вычитание двух чисел в десятичной системе счисления.
7. Что делают следующие программы для машины Поста?
Как будет работать каждая из программ при различных начальных состояниях ленты?
8. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в единичной системе счисления на единицу. Каретка расположена слева от числа.
9. Напишите программу для машины Поста, которая складывает два числа в единичной системе счисления. Каретка расположена над пробелом, разделяющим эти числа на ленте.
10. Что делают следующие НАМ, если применить их к символьной цепочке, состоящей из нулей и единиц?
Как будет работать каждая из программ при различных начальных состояниях ленты?
11. Напишите НАМ, который сортирует цифры двоичного числа так, чтобы сначала стояли все нули, а потом — все единицы.
12. Напишите: НАМ, который удаляет поглгдпий символ строки, состоящей из цифр 0 и 1. Какую операцию он выполняет, если рассматривать строку как двоичную запись числа.
13. Напишите НАМ, который умножает двоичное число на 2, добавляя О в конец записи числа.
Следующая страница 
Cкачать материалы урока