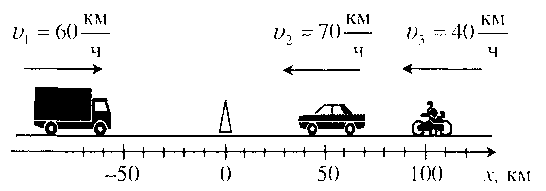
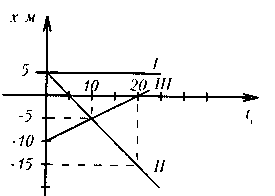Определите начальные координаты бензоколонки грузового и легкового автомобиля и мотоцикла запишите

Ввести понятие скорости как векторной величины. Научить описывать движение различными способами: графическим и координатным (как функцию от времени).

I. Повторение. Проверка домашнего задания

Повторение изученного можно провести в виде фронтального опроса либо проверочной самостоятельной работы по изученному материалу. Фронтальная беседа

— В чем состоит основная задача механики?

— Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой? Приведите примеры.

— Что такое система отсчета? Для чего она вводится?

— Какие виды систем координат вы знаете?

— Какую систему координат вы выберите для определения положения таких тел: стрекоза в полете, шахматная фигура на доске, теплоход движется на реке, лифт в доме, пуговица на одежде?

— Что такое траектория, путь, перемещение?

— В чем отличие пути от перемещения?

— В каком случае путь равен траектории? Приведите примеры.

— Подбросьте тело вверх и поймайте его при спуске. Что больше: путь тела или перемещение?

— Как определить проекцию вектора? (правило)

— Как определить проекцию вектора перемещения на ось?

Во время беседы на доске проверяется решение домашних задач.

Задания для самостоятельной работы:

1. Мяч падает с высоты 2 м, и, отскочив от земли, поднимается на высоту 1,5 м. Чему равны путь l и модуль перемещения S мяча? (Ответ: l = 3,5 м, S = 0,5 м.)

2. Материальная точка движется по окружности радиуса R. Чему равны путь l и модуль перемещения S через пол-оборота? (Ответ: l = πR, S = 2R.)

3. Укажите знаки проекций векторов на оси ОХ, ОY (рис. 9).

1. Мяч упал с высоты 4 м от пола и был пойман на высоте 2 м. Найти путь l и модуль перемещения S мяча. (Ответ: l = 6 м, S = 2 м.)

2. Автомобиль двигался по кольцевой дороге вокруг Москвы и дважды по ней проехал. Чему равны путь l и перемещение S, если длина кольцевой дороги L? (Ответ: путь l = 2L, перемещение S = 0.)

3. Укажите знаки проекций векторов на оси ОХ, OY (рис. 10).

На демонстрационном столе стоит стеклянная трубка, наполненная водой. При быстром се перевертывании пузырек воздуха начинает всплывать (можно открыть трубку и погрузить в жидкость какое-либо сферическое тело). Отмечая положения пузырька через равные промежутки времени (через 2 с), получаем таблицу:

Движение тела называется равномерным, если за любые равные промежутки времени тело перемещается на одинаковое расстояние (т. е. проходит одинаковые пути).

Как найти (вычислить) перемещение тела за какой-то промежуток времени t? Для этого надо знать перемещение тела за единицу времени. Это отношение называют скоростью и обозначают буквой :

При вычислении перемещения и скорости обычно пользуются формулами, в которые входят не векторы, а проекции векторов:

х₀— начальная координата [м],

Мы нашли зависимость координаты x от времени t, т. е. х(t).

Данная зависимость линейная. Из математики известно, что графиком линейной функции у = kx + b является прямая.

Далее можно рассмотреть различные варианты графиков зависимости координаты х от времени (при v_x = 0, v_x > 0, v_x

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Решение задач по теме «Скорость равномерного прямолинейного движения»

Продолжение решение задач

Просмотр содержимого документа
«Решение задач по теме «Скорость равномерного прямолинейного движения»»

Решение задач по теме «Скорость равномерного прямолинейного движения»

Задача 1. На рисунке показаны ось координат, тела и их скорости.

Определите начальные координаты грузового и легкового автомобиля и мотоцикла.

Запишите для каждого тела уравнение координаты.

Найдите когда и где встретятся:

Грузовой и легковой автомобили;

Грузовой автомобиль и мотоцикл.

З 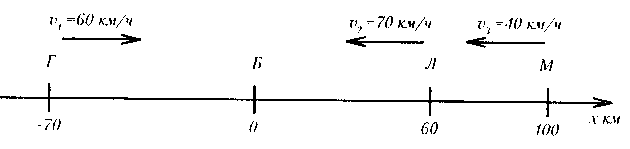адача 2. На рис. показаны ось координат тела и скорость.

Определите начальные координаты тел.

Запишите для каждого тела уравнение координат.

Найти, когда и где встретятся.

Продолжение решение задач

По заданным графикам найти:

начальные координаты тел;

проекции скорости движения тел;

написать уравнения движения тел х = х(t);

из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.

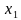
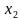
Движения двух велосипедистов заданы уравнениями; = 5t, = 150 — 10t. Построить графики зависимости x(t). Найти время и место встречи.

По прямому шоссе в одном направлении движутся два мотоциклиста. Ско­рость первого мотоциклиста 10 м/с. Второй догоняет его со скоростью 20 м/с. Рас­стояние между мотоциклистами в начальный момент времени равно 200 м. Напи­сать уравнения движения мотоциклистов в системе отсчета, связанной с землей, приняв за начало координат место нахождения второго мотоциклиста в началь­ный момент времени и выбрав за положительное направление оси X направление движения мотоциклистов. Построить на одном чертеже графики движения обоих мотоциклистов (рекомендуемые масштабы: в 1 см 100 м; в 1 см 5 с). Найти время и место встречи мотоциклистов.

Источник