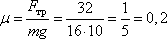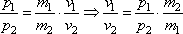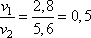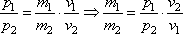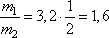Отношение импульса самосвала к импульсу легкового автомобиля p1 p2 2 каково отношение их скоростей

Подготовка учачихся 11 класса к экзаменам по физике

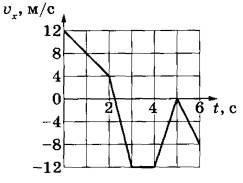
Задание 1. На рисунке показан график зависимости проекции vx скорости тела от времени. Какова проекция ax ускорения этого тела в интервале времени от 5 до 6 с?

Из графика видно, что на интервале от 5 до 6 с скорость меняется линейно, следовательно, тело двигалось с постоянным ускорением. В этом случае ускорение можно найти по формуле

м/с2

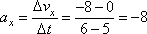
Задание 2. По горизонтальному полу по прямой равномерно тянут ящик массой 16 кг, приложив к нему горизонтальную силу 32 Н. Определите коэффициент трения скольжения между полом и ящиком.

Так как ящик тянут равномерно, то его ускорение равно 0. Тогда, согласно первому закону Ньютона, сила F=32 Н, приложенная к телу, лишь компенсирует силу трения и по модулю равна ей. Получаем следующее выражение:

,

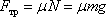
где μ – коэффициент трения; m = 16 кг – масса ящика; g – ускорение свободного падения. Находим μ:

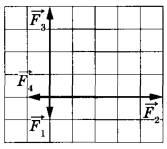
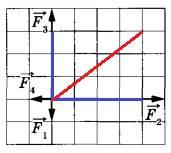
Задание 2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.

Сначала сложим силы F1 и F3. Так как они противоположно направлены, то получим результирующую силу, направленную как F3, но на одну клетку меньше. По аналогии сложим и силы F1 и F2. (см. синие линии на рисунке ниже).

Складывая полученные силы, имеем результирующую силу, направление которой показано красной линией на рисунке. Модуль этой силы найдем по теореме Пифагора из прямоугольного треугольника с катетами 4 и 3:

Н.

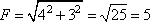
Задание 3. Отношение массы автобуса к массе легкового автомобиля m1/m2 = 5,6. Каково отношение их скоростей v1/v2, если отношение импульса автобуса к импульсу легкового автомобиля p1/p2 = 2,8?

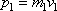
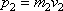
Импульс автобуса , а импульс автомобиля . Получаем выражение для отношения их скоростей:

и, подставляя числовые значения, имеем:

Задание 3. Отношение импульса автобуса к импульсу грузового автомобиля p1/p2 = 3,2. Каково отношение их масс m1/m2, если отношение скорости автобуса к скорости грузового автомобиля v1/v2 = 2?

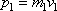
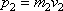
Импульс автобуса , а импульс автомобиля . Получаем выражение для отношения их масс:

и, подставляя числовые значения, имеем:

Задание 4. Период гармонических колебаний массивного груза на лёгкой пружине равен 1,2 с. В некоторый момент времени потенциальная энергия груза достигает максимума. Через какое минимальное время кинетическая энергия груза достигнет максимума?

Максимальное значение кинетическая энергия приобретает в точке равновесия пружины, когда скорость груза наибольшая. Так как период колебаний T=1,2 с, то эта точка равновесия из крайнего положения груза будет достигнута через T:4 = 1,2:4 = 0,3 с. Это легко установить, зная, что период колебаний – это время одного полного колебания, при котором груз дважды проходит точку равновесия пружины и первый раз он ее достигает через четверть периода (если начальное значение выбрать как крайнее отклонение груза).

Задание 5. В лаборатории исследовали прямолинейное движение тела массой m = 300 г из состояния покоя. В таблице приведена экспериментально полученная зависимость пути, пройденного телом, от времени.

Какие два вывода соответствуют результатам эксперимента?

1) Скорость тела в момент времени 4 с равнялась 4 м/с.

2) Кинетическая энергия тела в момент времени 2 с равна 2,4 Дж.

3) Первые 3 с тело двигалось равномерно, а затем оно двигалось равноускоренно.

4) За первые 3 с суммарная работа сил, действующих на тело, равна 10,8 Дж.

5) Равнодействующая сил, действующих на тело, была постоянна в течение всего времени наблюдения.

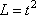
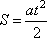
Из данных таблицы видно, что тело двигалось по закону и, учитывая, формулу равноускоренного движения тела , получаем, что здесь ускорение a=2 м/с2.

1) Скорость тела в момент времени t=4, равна 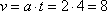м/с.

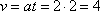
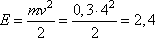
2) В момент времени t=2, скорость равна и кинетическая энергия тела Дж.

3) Нет, тело постоянно движется с ускорением a=2 м/с2.

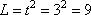
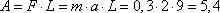
4) За первые 3 секунды тело прошло расстояние м и работа по перемещению тела, равна

Дж.

5) Да, так как в соответствии со вторым законом Ньютона F=ma, тело будет двигаться с одним ускорением, если на него постоянно действует одна и та же сила.

Задание 6. На поверхности воды плавает прямоугольный брусок из древесины плотностью 700 кг/м3. Брусок заменили на другой брусок той же массы и с той же площадью основания, но из древесины плотностью 400 кг/м3. Как при этом изменились глубина погружения бруска и действующая на него сила Архимеда?

Для каждой величины определите соответствующий характер изменения:

Так как масса брусков в обоих случаях одинакова и они оба плавают в воде (их плотность ниже плотности воды в 1000 кг/м3), то на них будет действовать одна и та же сила Архимеда, компенсирующая силу их тяжести F=mg.

При уменьшении плотности бруска его объем должен возрастать, чтобы обеспечить ту же массу, что и у первого бруска с большей плотностью ( ). Так как площади основания у них равны, то второй брусок будет выше первого. Сила Архимеда зависит от объема погруженной части тела: . Учитывая, что силы Архимеда в обоих случаях равны, то и объем погруженной части брусков также должен быть одинаков. А так как площади основания у них равны, то и их глубина погружения будет одинаковой.

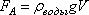
Задание 7. Материальная точка движется по оси х. Её скорость меняется по закону: .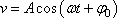

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

А) период колебаний материальной точки Т

Б) амплитуда ускорения точки

А) Период колебаний связан с циклической частотой ω выражением:

Б) Ускорение – это производная от скорости по времени:

и ее максимальное значение будет равно ωA.

Задание 8. Концентрацию молекул идеального одноатомного газа увеличили в 4 раза. Одновременно в 2 раза уменьшили абсолютную температуру газа. Во сколько раз в результате этого увеличилось давление газа в сосуде?

Давление возникает в результате столкновения частиц газа со стенками сосуда. Если концентрацию этих частиц увеличить в 4 раза (а все остальные условия эксперимента оставить неизменными), то давление возрастет в 4 раза.

В итоге получаем, сначала давление увеличивается в 4 раза, а затем, уменьшается в 2 раза, то есть, имеем p2=4p/2=2p – возрастет в 2 раза.

Задание 9. На рисунке показан циклический процесс изменения состояния 1 моль одноатомного идеального газа. На каком участке цикла работа внешних сил над газом равна отданному газом количеству теплоты?

Согласно первому закону термодинамики

количество отданного тепла Q будет равно работе внешних сил A при ∆U=0. Изменение внутренней энергии газа ∆U=0 когда температура газа T=const и его масса остается постоянной. Это соответствует процессу 1.

Задание 10. На сколько градусов нагреется медная деталь массой 500 г, если ей сообщить количество теплоты, равное 380 Дж?

Величину изменения температуры медной детали массой m=0,5 кг с удельной теплоемкостью c = 380 Дж/(кг∙С) при затрате количества теплоты Q = 380 Дж можно найти по формуле:

Задание 11. На pV-диаграмме показаны два процесса, проведённые с одним и тем же количеством газообразного неона.

Из приведённого ниже списка выберите два правильных утверждения, характеризующих процессы на графике.

1) В процессе 2 абсолютная температура неона изобарно уменьшилась в 2 раза.

2) В процессе 1 плотность неона уменьшилась в 5 раз.

3) В процессе 1 неон изотермически увеличил свой объём в 5 раз.

4) В процессе 2 концентрация молекул неона увеличилась в 2 раза.

5) Работа, совершённая неоном в процессе 1, равна работе, совершённой в процессе 2.

1) Изобарный процесс – это процесс, протекающий при постоянном давлении и массе вещества. В процессе 2 давление p газа постоянно, а объем V увеличился. Следовательно, из уравнения состояния идеального газа следует, что температура T изобарно увеличилась.

2) В процессе 1 имеем увеличение объема. При сохранении массы m газа, его плотность уменьшается. Учитывая, что объем увеличился в 5 раз, то плотность уменьшилась в пять раз.

3) Изотермический процесс – это процесс протекающий при постоянной температуре. Процесс 1 протекает при постоянном давлении p, следовательно, увеличение объема V возможно только за счет увеличения температуры T (следует из уравнения pV/T = const).

4) В процессе 2 происходит увеличение объема при постоянной массе, следовательно, число молекул на единицу объема уменьшается.

5) Работу, совершенную газом, можно найти как величину площади под графиком p(V). Из рисунка видно, что эта площадь одинакова для обоих процессов.

Задание 12. С постоянным количеством газа провели процесс a→b→c→d→e→f, в течение которого вычисляли внутреннюю энергию U газа и измеряли работу A, совершённую газом от момента начала процесса. AU-диаграмма процесса приведена на рисунке.

Установите соответствие между названием процесса и участком на диаграмме, на котором он представлен.

А) адиабатное сжатие

Б) адиабатное расширение

УЧАСТОК НА ДИАГРАММЕ

Адиабатический процесс – это процесс, при котором система не обменивается теплотой с окружающим пространством.

А) При адиабатическом сжатии над газом совершают работу, то есть, A

Б) При адиабатическом расширении газ совершает работу, то есть, A 0. Внутренняя энергия газа уменьшается вследствие уменьшения температуры. Имеем участок b-c под номером 1.

На рисунке синяя линия показывает результирующую силу, действующую на заряд 2q, которая направлена влево.

Задание 14. По участку цепи (см. рисунок) течёт постоянный ток I = 8 А. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.

Ток в точке ветвления распределяется обратно пропорционально сопротивлениям ветвей. Из рисунка видно, что верхний участок цепи параллельного соединения состоит из трех сопротивлений r, а нижний – из одного сопротивления r. Следовательно, ток будет делиться в отношении 1:3 в пользу нижней цепи. То есть, амперметр будет показывать значение

Задание 15. На рисунке приведён график зависимости силы тока I от времени t в электрической цепи, содержащей катушку, индуктивность которой 2 мГн. Определите модуль ЭДС самоиндукции в катушке в интервале времени от 15 до 20 с.

Модуль ЭДС самоиндукции можно определить по формуле

Из графика видно, что за время ∆t=20-15=5 секунд сила тока изменилась на величину ∆I=0-20=-20 мА. Следовательно, ЭДС самоиндукции равна

что составляет 8 мкВ.

Задание 16. В идеальном колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.

Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях:

1) заряд конденсатора

2) частота колебаний силы тока в контуре

3) фаза колебаний напряжения на конденсаторе

4) амплитуда колебаний заряда на конденсаторе

5) энергия электрического поля конденсатора

1) Заряд конденсатора постоянно меняется: сначала уменьшается, затем, снова увеличивается.

2) Да, частота колебаний силы тока в идеальном колебательном контуре остается постоянной.

4) Да, амплитуда колебаний заряда остается прежней, так как в идеальном колебательном контуре заряд никуда не исчезает.

5) Энергия электрического поля конденсатора периодически то уменьшается, то увеличивается.

Задание 17. В прозрачном сосуде с водой находится дифракционная решётка, которая освещается параллельным пучком монохроматического света, падающим на решётку перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, падающей на решётку, и угол между падающим лучом и направлением на второй дифракционный максимум, если воду заменить прозрачной жидкостью с меньшим показателем преломления?

Для каждой величины определите соответствующий характер изменения:

Задание 18. В прозрачном сосуде, заполненном водой, находится дифракционная решетка. Решетка освещается параллельным пучком монохроматического света, падающим перпендикулярно ее поверхности через боковую стенку сосуда. Как изменятся частота световой волны, падающей на решетку, и угол между падающим лучом и первым дифракционным максимумом при замене воды в сосуде прозрачной жидкостью с большим показателем преломления?

Для каждой величины определите соответствующий характер изменения:

Частота света останется неизменной при переходе из одной среды в другую, меняется ее длина и скорость. Длина волны связана со скоростью и частотой колебаний выражением

Угол отклонения лучей и первым дифракционным максимумом связан выражением

Задание 18. Заряженная частица массой m, несущая положительный заряд q, движется перпендикулярно линиям индукции однородного магнитного поля B по окружности со скоростью v. Действием силы тяжести пренебречь.

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

А) радиус окружности, по которой обращается частица

Б) частота обращения частицы по окружности

Длина окружности, по которой движется частица, составляет

Период обращения частицы (время прохождения одного круга):

и частота обращения частицы, равна

Согласно закону сохранения зарядовых и массовых чисел, можно записать следующую систему для заданной ядерной реакции:

Дан период полураспада T=164 суток и время распада t=328 дней. Пусть начальный объем кальция составляет %, получим оставшийся объем:

Задание 21. Монохроматический свет с энергией фотонов Eф падает на поверхность металла, вызывая фотоэффект. При этом напряжение, при котором фототок прекращается, равно Uзan. Как изменятся длина волны λ падающего света и модуль запирающего напряжения Uзan, если энергия падающих фотонов Еф увеличится?

Для каждой величины определите соответствующий характер изменения:

Запирающее напряжение зависит от величины кинетической энергии фотоэлектронов. При увеличении энергии падающих фотонов, максимальная кинетическая энергия фотоэлектронов также возрастает (работа выхода остается неизменной). Следовательно, для удержания фотоэлектронов с большей энергией потребуется и более высокое запирающее напряжение.

Длина волны падающего света связана с энергией фотонов, выражением:

то есть, при увеличении E, длина волны λ уменьшается.

Задание 22. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?

Из рисунка видно, что цена деления динамометра равна (1,5-1):5 = 0,1 Н. Стрелка показывает отметку в 1,1 Н. Получаем результаты измерений:

Задание 23. Необходимо экспериментально изучить зависимость сопротивления проводника от площади поперечного сечения проводника.

Какие два проводника следует использовать для проведения такого исследования?

Необходимо выбрать проводники из одного материала и одинаковыми длинами, но с разными площадями поперечного сечения. Этим условиям удовлетворяют проводники под номерами 3 и 5.

Задание 24. На рисунке представлена диаграмма Герцшпрунга-Рессела.

Выберите два утверждения о звёздах, которые соответствуют диаграмме.

1) Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, а значит, она относится к звёздам главной последовательности.

2) Плотность белых карликов существенно выше средней плотности гигантов.

3) «Жизненный цикл» звезды спектрального класса О главной последовательности более длительный, чем звезды спектрального класса F главной последовательности.

4) Температура поверхности звёзд спектрального класса А выше температуры поверхности звёзд спектрального класса G.

5) Звёзды спектрального класса А имеют температуру поверхности не выше 5000 К.

1) Из диаграммы видно, что звезды с радиусом почти в 1000 раз превышающие радиус Солнца, не принадлежат главной последовательности.

2) Как видно из диаграммы белые карлики имеют диаметр порядка 0,01 солнечного, а гиганты — 10 солнечных. Т. е. диаметр белых карликов в 1000 раз меньше, чем у гигантов. Чтобы иметь среднюю плотность меньше, чем у гигантов, массы белых карликов должны быть в миллиард ( ) раз меньше. Но это не так. Массы белых карликов сравнимы с массой Солнца, а массы гигантов только в десятки раз превышают солнечные. Таким образом, наоборот, плотность белых карликов существенно больше средней плотности гигантов.

3) «Жизненный цикл» звезды спектрального класса О главной последовательности меньший, чем у звезд спектрального класса F главной последовательности.

4) Температура звёзд спектрального класса G меньше температуры звёзд спектрального класса А.

5) Звёзды спектрального класса А имеют температуру поверхности заметно выше 5000 К.

Задание 25. На рисунке показан график зависимости давления 3 моль газа в запаянном сосуде от его температуры. Каков приблизительно объём сосуда? Ответ округлите до сотых.

Найдем объем сосуда из уравнения Менделеева-Клапейрона:

где v=3 моль; R=8,31 – универсальная газовая постоянная; T = 300 К – температура газа; Па. Подставляя эти значения в формулу, получаем:

Задание 26. При облучении фотокатода светом частотой Гц запирающее напряжение для фотоэлектронов равно 0,60 В. Найдите работу выхода фотоэлектронов из материала катода. Ответ выразите в электрон-вольтах.

Запишем уравнение Эйнштейна для фотоэффекта

где A – работа выхода; E – кинетическая энергия выбиваемых фотоэлектронов. Запирающее напряжение U связано с кинетической энергией E выражением:

где Кл – заряд электрона. Находим работу выхода:

Так как 1 эВ = Дж, то получаем работу выхода

Источник

Задания для подготовки к ЕГЭ по физике(А3)

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Задание 3.1. Мячик массой 0,2 кг, брошенный вертикально вверх, достиг максимальной высоты 7 м. Какой кинетической энергией обладал мячик сразу после броска? Сопротивлением воздуха пренебречь.

На максимальной высоте h=7 м вся начальная кинетическая энергия Eк мячика перешла в потенциальную энергию Eп = mgh, то есть,

Задание 3.2. Камень массой 0,15 кг бросили вертикально вверх. На какую максимальную высоту поднялся камень, если сразу после броска его кинетическая энергия составила 6 Дж? Сопротивлением воздуха пренебречь.

На максимальной высоте вся начальная кинетическая энергия переходит в потенциальную энергию камня:

,

м.

Задание 3.3. Отношение скорости автобуса к скорости легкового автомобиля v1/v2 = 1/3. Масса автобуса m1 = 7200 кг. Какова масса легкового автомобиля, если отношение импульса автобуса к импульсу легкового автомобиля равно 1,6?

Импульс автобуса равен , а импульс автомобиля . По условию, их отношение равно

.

Выразим массу автомобиля, имеем:

кг.

Задание 3.4. Отношение массы трамвая к массе автобуса m1/m2 = 3. Скорость трамвая v1 = 10 м/с. Какова скорость автобуса, если отношение импульса трамвая к импульсу автобуса равно 2?

Импульс трамвая обозначим через , а импульс автобуса через . По условию задания , откуда . Так как , получаем:

м/с.

Задание 3.5. Девочка бросила мяч массой 0,5 кг вертикально вверх с высоты 0,8 м над поверхностью Земли. Мяч поднялся на высоту 3 м от поверхности Земли. Каково изменение потенциальной энергии мяча?

Потенциальная энергия тела массой m на высоте h определяется как . Изначально тело массой 0,5 кг было брошено на высоте 0,8 м, его потенциальная энергия была равна Дж. На максимальной высоте 3 м потенциальная энергия стала равна Дж. Следовательно, изменение потенциальной энергии составило

Задание 3.6. Девочка бросила мяч массой 0,3 кг вертикально вниз с высоты 1,3 м над поверхностью Земли. Мяч ударился о Землю и поднялся на высоту 2,5 м от поверхности Земли. Каково изменение потенциальной энергии мяча при переходе из начального положения в конечное?

Значение потенциальной энергии в начальный момент можно вычислить по формуле , где h1 = 1,3 м – начальное значение высоты. После отскока мяч поднялся на высоту h2 = 2,5 м где его потенциальная энергия составила . Таким образом, изменение потенциальной энергии составило:

Задание 3.7. Отношение импульса автокрана к импульсу легкового автомобиля p1/p2 = 1,8. Каково отношение их масс m1/m2, если отношение скорости автокрана к скорости легкового автомобиля v1/v2 = 0,3?

Импульс крана – это величина , а импульс легкового автомобиля – . Отношение этих величин дает

,

.

Задание 3.8. Отношение импульса самосвала к импульсу легкового автомобиля p1/p2 = 2. Каково отношение их скоростей v1/v2, если отношение массы самосвала к массе легкового автомобиля m1/m2 = 12,5?

Найдено решение такого же или подобного задания

Задание 3. Отношение импульса автокрана к импульсу легкового автомобиля p1/p2 = 1,8. Каково отношение их масс m1/m2, если отношение скорости автокрана к скорости легкового автомобиля v1/v2 = 0,3?

Импульс крана – это величина , а импульс легкового автомобиля – . Отношение этих величин дает

,

.

Задание 3.9. Шарик массой 100 г падает с высоты 10 м нулевой начальной скоростью. К моменту падения на землю потеря полной механической энергии за счёт сопротивления воздуха составила 10 %. Какова кинетическая энергия шарика в этот момент?

На высоте h = 10 м потенциальная энергия шарика равна

Дж.

При падении 90% этой потенциальная энергии переходит в кинетическую, то есть, кинетическая энергия, равна:

Дж.

Задание 3.10. Мячик массой 200 г падает с некоторой высоты с нулевой начальной скоростью. К моменту падения на землю его кинетическая энергия равна 24 Дж. С какой высоты падал мячик, если потеря полной механической энергии за счёт сопротивления воздуха составила 20%?

К моменту удара о землю кинетическая энергия шарика составила 24 Дж, что составляет 80% от начальной потенциальной энергии, то есть, потенциальная энергия на максимальной высоте была равна

Дж.

Учитывая, что потенциальная энергия равна , находим максимальную высоту h:

м.

Задание 3.11. Легковой автомобиль и грузовик движутся по мосту. Масса легкового автомобиля m = 1000 кг. Какова масса грузовика, если отношение значений потенциальной энергии грузовика и легкового автомобиля относительно уровня воды равно 4?

Потенциальная энергия автомобиля массой m=1000 кг относительно уровня воды h, равна . Потенциальная энергия грузовика массой M относительно того же уровня воды h, равна . Так как , имеем:

и масса грузовика равна

кг.

Задание 3.12. Легковой автомобиль и грузовик движутся по мосту. Каково отношение массы грузовика к массе легкового автомобиля, если отношение значений их потенциальной энергии относительно уровня воды равно 3?

Потенциальная энергия грузовика относительно уровня h воды, равна

,

а потенциальная энергия автомобиля на этом же уровне h

.

В задаче сказано, что , то есть

.

Задание 3.13. Тело движется по прямой. Начальный импульс тела равен 60 кг • м/с. Под действием постоянной силы величиной 10 Н, направленной вдоль этой прямой, за 5 с импульс тела уменьшился. Определите импульс тела в конце указанного промежутка времени.

Импульс тела определяется как , где m – масса тела; v – скорость тела. Под действием силы F=10 Н в соответствии со вторым законом Ньютона телу было сообщено ускорение, равное

,

которое длилось t=5 секунд. Следовательно, скорость тела уменьшилась на

и импульс стал равен

,

.

Задание 3.14. Тело движется по прямой в одном направлении под действием постоянной силы, равной по модулю 10 Н и направленной вдоль этой прямой. Сколько времени потребуется для того, чтобы под действием этой силы импульс тела изменился на 50 кг•м/с?

Тело движется под действием силы F=10 Н, следовательно, оно движется с ускорением

.

Импульс тела определяется выражением . Отсюда видно, что увеличение импульса происходит за счет увеличения скорости, то есть при определенном изменении скорости , импульс должен измениться на величину . Изменение скорости осуществляется за счет ускорения , то есть можно записать, что

,

или, умножая левую и правую части уравнения на m, имеем:

,

секунд.

Задание 3.15. Координата тела массой 8 кг, движущегося вдоль оси x, изменяется по закону x = x0 + vx*t, где x0 = 6 м; vx = 8 м/с. Кинетическая энергия тела в момент времени t = 2 с равна

Кинетическая энергия тела определяется по формуле и так как тело движется с постоянной скоростью 8 м/с, то она остается постоянной и равна

Дж.

Дж.

Задание 3.17. Мальчик массой 50 кг находится на тележке массой 50 кг, движущейся по гладкой горизонтальной дороге со скоростью 1 м/с. Каким станет модуль скорости тележки, если мальчик прыгнет с неё со скоростью 2 м/с относительно дороги в направлении, противоположном первоначальному направлению движения тележки?

Обозначим через m=50 кг массу мальчика, а через M=50 кг – массу тележки. Тогда начальный импульс тележки с мальчиком будет равен , где м/с – начальная скорость тележки с мальчиком. Согласно закону сохранения импульса, суммарный импульс прыгающего с тележки мальчика и самой тележки должны быть равны исходному импульсу , то есть имеем:

,

(здесь знак «-» показывает, что вектор скорости мальчика направлен в противоположную сторону вектора скорости тележки). Из этой формулы находим скорость тележки:

м/с.

Задание 3.18. Мальчик массой 50 кг находится на тележке массой 100 кг, движущейся по гладкой горизонтальной дороге со скоростью 1 м/с. Каким станет модуль скорости тележки, если мальчик прыгнет с неё со скоростью 3 м/с относительно дороги в направлении, противоположном первоначальному направлению движения тележки?

Обозначим через m=50 кг массу мальчика, а через M=100 кг – массу тележки. Тогда начальный импульс тележки с мальчиком будет равен , где м/с – начальная скорость тележки с мальчиком. Согласно закону сохранения импульса, суммарный импульс прыгающего с тележки мальчика и самой тележки должны быть равны исходному импульсу , то есть имеем:

,

(здесь знак «-» показывает, что вектор скорости мальчика направлен в противоположную сторону вектора скорости тележки). Из этой формулы находим скорость тележки:

м/с.

Задание 3.19. При упругой деформации 1 см стальная пружина имеет потенциальную энергию 1 Дж. На сколько увеличится потенциальная энергия этой пружины при увеличении деформации ещё на 1 см?

Потенциальная энергия упругой деформации сжатой (или растянутой) на x метров пружины с жесткостью k, определяется по формуле

.

Изначально деформация составляла x=0,01 м и потенциальная энергия была равна

Дж.

При увеличении деформации на 0,01 м, то есть при x=0,02 м потенциальная энергия станет равной

Дж,

то есть увеличится в 4 раза и станет

Дж,

то есть потенциальная энергия изменится на

Дж.

Задание 3.20. При упругой деформации 2 см стальная пружина имеет потенциальную энергию 4 Дж. Насколько уменьшится потенциальная энергия этой пружины при уменьшении деформации на 1 см?

Потенциальная энергия пружины определяется формулой , где x=0,02 м – деформация пружины; k – жесткость пружины. Найдем отсюда жесткость пружины

Н/м.

При уменьшении деформации на 1 см = 0,01 м ее потенциальная энергия изменится на величину

Дж.

Задание 3.21. Материальная точка движется в инерциальной системе отсчёта по прямой в одном направлении. За 5 с импульс тела увеличивается на 15 кг∙м/с. Чему равен модуль равнодействующей сил, приложенных к телу?

Импульс тела определяется как p=mv, где m – масса тела; v – скорость тела. В задаче сказано, что за время t=5 с импульс увеличивается на 15. Так как масса тела остается неизменной, то увеличение импульса происходит за счет увеличения скорости, то есть

,

и ускорение, с которым двигалось тело, равно

.

Равнодействующая сил, приложенных к телу, равна F=ma или в виде

Н.

Задание 3.22. Материальная точка движется в инерциальной системе отсчёта по прямой в одном направлении. За 3 с импульс тела увеличивается на 24 кг • м/с. Чему равен модуль равнодействующей сил, приложенных к телу?

Тело меняет свой импульс под действием равнодействующей силы F=ma, откуда ускорение тела равно . Тогда за t=3 с скорость тела изменится на величину . Изменение импульса или в виде

,

откуда равнодействующая сила равна

Н.

,

.

,

откуда получаем скорость платформы

м/с.

Задание 3.25. Охотник, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,04 кг. Скорость дробинок при выстреле 300 м/с. Какова масса охотника, если его скорость после выстрела равна 0,2 м/с?

Импульсы пули и охотника до выстрела равны нулю, так как они обладают нулевой скоростью. После выстрела импульс дробинок равен , где кг – масса заряда; м/с – скорость дробинок. Импульс охотника , где — масса охотника; м/с – скорость охотника. Так как движение дробинок и охотника противоположно, то сумма их импульсов запишется со знаком «-», то есть:

,

и масса охотника равна

кг.

Задание 3.26. Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле 300 м/с. Какова скорость охотника после выстрела?

,

откуда скорость охотника равна

м/с.

Задание 3.27. В инерциальной системе отсчёта тело движется по прямой в одном направлении под действием постоянной силы, равной по модулю 10 Н. Сколько времени потребуется для того, чтобы под действием этой силы импульс тела изменился на 50 кг • м/с?

Чтобы импульс тела изменился на 50, необходимо, чтобы его скорость изменилась на 50 м/с, так как изменение импульса это величина . Тело движется под действием постоянной силы F=ma, то есть с ускорением . Под действием этого ускорения, скорость тела изменится на 50 м/с за время . Подставляя вместо ускорения указанное выражение, получаем:

с.

Задание 3.28. В инерциальной системе отсчёта тело движется по прямой в одном направлении под действием постоянной силы в течение 5 с. Определите модуль силы, если за это время под действием этой силы импульс тела изменился на 30 кг∙м/с.

Изменение импульса тела происходит за счет изменения скорости тела, то есть . В свою очередь, изменение скорости тела за время t=5 с это величина, равная , где ускорение в соответствии со вторым законом Ньютона. Объединяя эти выражения, получаем:

,

откуда величина силы

Н.

Согласно закону сохранения импульсов импульс до разрыва p0 должен быть равен суперпозиции импульсов после разрыва снаряда. Под это определение вместе с импульсом p1 подходит вектор импульса 1, так как их суперпозиция в точности равна импульсу p0.

Согласно закону сохранения импульсов импульс до разрыва p0 должен быть равен суперпозиции импульсов после разрыва снаряда. Под это определение вместе с импульсом p1 подходит вектор импульса 1, так как их суперпозиция в точности равна импульсу p0.

Источник