Передний управляемый мост автомобиля
Мост автомобиля. Очень интересная статья! Забери статью к себе!
Мост объединяет между собой два колеса автомобиля на одной оси, соединяет колеса с кузовом, а в случае, если мост ведущий, передает на колеса крутящий момент.
— Мост, особенно ведущий — сложный узел из множества деталей, выполняющих разные функции. В картере ведущего моста расположены: главная пара, дифференциал и полуоси. Мост воспринимает на себя все вертикальные, поперечные и продольные нагрузки, которые гасятся упругими элементами подвески — рессорами или пружинами.
Соответственно, мост не имеет жесткой связи с кузовом (рамой) и соединяется с ним при помощи рессор с реактивными тягами или рычагов с пружинами, в зависимости от конструкции. По сути, мост как бы висит на этих элементах, соединенных с кузовом или рамой через резинометаллические втулки.
Типы автомобильных мостов
1)Ведущие
2)Управляемые
3)Управляемые ведущие
4)Поддерживающие
Ведущие мосты бывают передними, задними и промежуточными. Они также делятся на неразрезные и разрезные — в зависимости от типа подвески. Если автомобиль оснащен независимой подвеской, ведущий мост делается разрезным, если подвеска зависимая, мост, как правило, неразрезной.
На легковых автомобилях классической компоновки задний мост ведущий, на полноприводных автомобилях ведущие оба моста.
Когда речь идет об управляемом мосте, в подавляющем большинстве случаев имеется в виду передний мост автомобиля с задним или полным приводом. Однако у автомобилей специального назначения (автомобили коммунальных служб, сельскохозяйственная колесная техника, погрузчики др.) передний мост может быть ведущим, а задний мост – управляемым.
Поддерживающий мост применяется в качестве промежуточного для повышения грузоподъемности автомобиля и служит дополнительным элементом в схеме распределения вертикальной нагрузки на раму или несущий кузов. Такой мост представляет собой прямую балку, на концах которой смонтированы колеса, оснащенную подвеской. Поддерживающие мосты также нашли применение в крупных и тяжелых полуприцепах и прицепах для легковых автомобилей и пикапов (например в «доме на колесах»).
Неразрезной ведущий мост
Конструктивно такой мост выполняется пустотелым в виде балки, для размещения в ней узлов трансмиссии: дифференциала, главной пары и полуосей, являющихся приводом к ведущим колесам автомобиля. На концах балки установлены подшипники полуосей и смонтированы фланцы для крепления опорных дисков и тормозных механизмов. На теле балки выполнены площадки под крепления рессор или пружин, а также кронштейны для соединения с подвеской.
Назначение ведущего моста заключается в изменении подведенного крутящего момента и передачи его под прямым углом на ведущие колеса. При прохождении поворота ведущий мост дает возможность ведущим колесам автомобиля вращаться с различными скоростями. Мост также передает тяговое усилие и реактивный момент к раме или несущему кузову автомобиля от ведущих колес, а также воспринимает силу веса и боковые реакции, при движении автомобиля в повороте.
Конструкция неразрезного заднего моста
Задний мост автомобиля включает в себя следующие элементы: картер заднего моста, дифференциал, главную передачу и полуоси привода колес. Картер заднего моста служит для установки необходимых узлов с их заданным взаимным расположением, передающих крутящий момент к ведущим колесам. Вместе с тем картер заднего моста одновременно является элементов подвески задних колес, воспринимающий через подвеску вес автомобиля, передающийся на колеса.
Картер заднего моста выполнен методом штамповки. На концах картера запрессованы и приварены стальные кованые фланцы, которые окончательно обрабатываются после сварки. Фланцы имеют специальные гнезда для установки подшипников полуосей и резьбы для крепления тормозного щита.
В средней части картера моста имеется отверстие впереди для установки редуктора заднего моста (главная передача), а сзади это отверстие закрыто штампованной приваренной крышкой. В крышке расположено маслозаливное отверстие под резьбовую пробку. Снизу картера имеется отверстие для слива масла, которое также закрывается резьбовой пробкой. Обычно в пробке имеется магнитный элемент для сбора металлических продуктов износа, которые удаляются с пробки при смене масла в редукторе.
Подводимое к заднему мосту усилие (крутящий момент) от двигателя через карданную передачу увеличивается главной передачей в редукторе. Помимо этого главная передача изменяет положение оси вращения на 90 градусов посредством передачи момента через шестерни дифференциала на полуоси.
Полуоси выполнены из углеродистой стали 40 и по всей длине закалены ТВЧ для придания им упругих свойств и увеличения их прочности. На концах полуосей имеются отлитые воедино с ней фланцы, к которым крепятся тормозные механизмы и колеса. Внутренняя часть полуосей имеет накатанные шлицы, входящие в зацепление с шестернями дифференциала.
Управляемый мост автомобиля может быть как разрезным, так и не разрезным.
Неразрезной мост представляет собой балку с поворотными кулаками на концах, что обеспечивает возможность поворота управляемых колес при движении автомобиля. На цапфах поворотных кулаков крепятся через ступицы управляемые колеса.
Балка моста одновременно должна быть легкой, прочной и жесткой. Таким условиям отвечают в наибольшей степени, кованные стальные балки двутаврового сечения. На балке предусмотрены опорные площадки для крепления элементов подвески.
Балка в своей средней части выгнута вниз, для того чтобы расположить двигатель как можно ниже, что позволяет сместить центр тяжести для повышения устойчивости автомобиля.
Передний разрезной управляемый мост
Разрезной мост это закрепленный на подрамнике редуктор с приводными валами, передающими крутящий момент колесам. Независимая подвеска соединяется с поворотными кулаками, как это бывает у переднеприводных автомобилей. Управляемые колеса, прикрепленные к ступицам, могут поворачиваться вместе со стойками, обеспечивая автомобилю возможность маневрировать.
Передний управляемый мост



Передний управляемый мост представляет собой поперечную балку, к которой шарнирно закрепляются поворотные цапфы управляемых колес. Крутящий момент к таким мостам не подводится и они поддерживают несущую часть автомобиля и обеспечивают его поворот. Применяются эти мосты на легковых и грузовых автомобилях с колесными формулами 4×2, 6×2 и 6×4.
Рис. 6.5. Передние управляемые мосты: а – с неразрезной балкой; б – с разрезной балкой; 1 – колеса; 2 – поворотная цапфа; 3 – поворотный шкворень; 4 – балка; 5 – рессора; 6 – стойка; 7 – пружина подвески
В зависимости от типа подвески передних колес управляемые мосты могут быть неразрезные и разрезные. Неразрезные управляемые мосты (рис. 6.5, а) устанавливаются на автомобилях с передней зависимой подвеской. В таких мостах колеса непосредственно связаны с балкой и перемещение одного колеса в вертикальном направлении влияет на перемещение другого колеса. При разрезной балке (рис. 6.5, б) управляемые колеса с ней не связаны и их перемещение в вертикальном направлении не зависимо друг от друга.
Передний управляемый неразрезной мост (рис. 6.5, а) представляет собой балку 4 с установленными по концам поворотными цапфами 2. Такие балки изготавливают методом ковки из углеродистых сталей обычно двутаврового сечения. Средняя часть балки выгнута вниз, что позволяет ниже расположить двигатель, понизить центр массы автомобиля, за счет чего повысить его устойчивость. В бобышках балки неподвижно закреплены поворотные шкворни 3, с которыми, в свою очередь, соединены поворотные цапфы 2. На поворотных цапфах на подшипниках устанавливаются ступицы передних колес 1. За счет поворота цапф вокруг шкворней обеспечивается управление автомобилем на поворотах. Соединение моста с несущей частью автомобиля производится с помощью рессор 5.
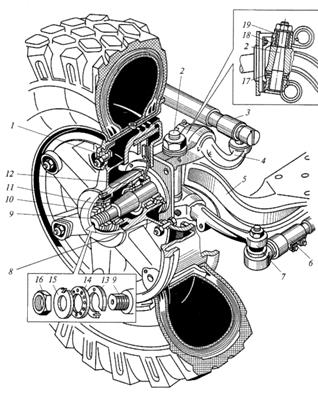
Конструкция переднего управляемого моста с неразрезной балкой автомобиля МАЗ приведена на рис. 6.6. Балка 5 такого моста кованная из стали с двутавровым сечением с прогибом вниз в средней части. С поворотными цапфами 9 балка соединена поворотными шкворнями 2, имеющими в средней части конусную форму. Шкворни 2 ступенчатого диаметра установлены в вильчатых поворотных цапфах 9 на бронзовых втулках 19 и закреплены гайками. В нижней части обоих поворотных цапф закреплены поворотные рычаги 7 и верхний поворотный рычаг 4 только в левой цапфе. На цапфах на двух роликовых подшипниках 11 и 12 установлены ступицы 8 с тормозными барабанами и колесами. Подшипники колес закреплены с помощью гайки 13, кольца 14, шайбы 15 и контргайки 16. С помощью этих крепежных деталей осуществляется регулировка затяжки пошипников колес.
Передний разрезной мост (рис. 6.5, б) представляет собой балку или поперечину (подрамник) 4 с прикрепленной к ней с обоих сторон подвеской колес 7 и управляемыми колесами 1. Балка или поперечина крепится к кузову автомобиля и предназначена для закрепления на ней двигателя. Установка передних колес может быть шкворневая или бесшкворневая. В первом случае поворот управляемых колес осуществляется вокруг шкворня, во втором случае – вокруг поворотной стойки 6.
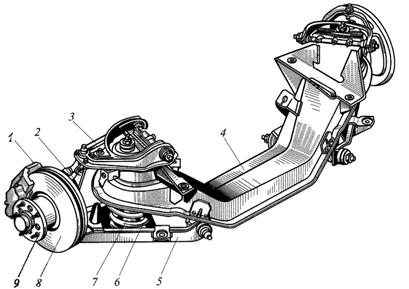
На рис. 6.7 приведен передний управляемый мост с разрезной балкой легкового автомобиля с независимой бесшкворневой подвеской. Основной деталью моста является поперечина 4, изготовленная в виде штампосварной конструкции из листовой стали с выгнутой вниз средней частью. К поперечине 4 с помощью верхнего 3 и нижнего 5 рычагов подвески, стоек 2, пружин 6 и амортизаторов 7 подвешены передние управляемые колеса. Весь передний мост в сборе может быть закреплен к кузову автомобиля.
Для создания наименьшего сопротивления движению, уменьшения износа шин, снижения расхода топлива, обеспечения стабилизации управляемых колес оси шкворней (или оси поворота) и колеса устанавливают с определенными углами в пространстве.
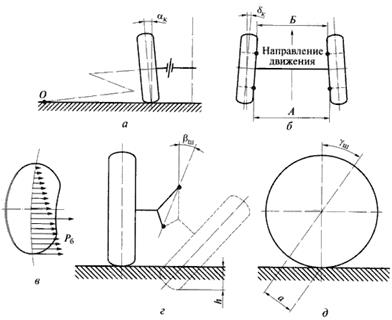
Углы установки шкворней (осей поворота) и управляемых колес приведены на рис. 6.8. Управляемые колеса устанавливаются с развала αк (рис. 6.8, а), чтобы обеспечить вертикальное положение колес по отношению к дороге под нагрузкой при деформации деталей переднего моста. Угол развала на автомобилях различного типа и класса выбирается в пределах 0…2 0 и обеспечивается соответствующим наклоном поворотной цапфы. по отношению к балке моста. В эксплуатации за счет износа подшипников колес и втулок шкворней этот угол может изменятся. поэтому в конструкции передних управляемых мостов предусматривается регулировка развала колес.
Рис. 6.8. Схема установки (а, б) и стабилизации (в, г, д) управляемых колес автомобиля
В совокупности углы развала и схождения управляемых колес обеспечивают минимальное их боковое скольжение и износ шин.
Комбинированный мост
Комбинированный мост выполняет одновременно функции ведущего и управляемого мостов. Комбинированный мост (рис. 6.9, а) включает в себя балку моста, главную передачу 1, дифференциал 2, привод на ведущие колеса 3, 4, 5 и ступицы колес 6.
При зависимой подвеске (рис. 6.9, а, б) комбинированный мост имеет неразрезную балку и привод ведущих колес виде шарнира равных угловых скоростей. Крутящий момент от дифференциала 2 к карданному шарниру 4 передается через внутреннюю полуось 3; далее от карданного шарнира равных угловых скоростей крутящий момент передается на внешнюю полуось 5 и ступицу колеса 6, установленную на полуосевом рукаве на подшипниках.
При независимой подвеске (рис. 6.9, в) используются карданные передачи с двумя шарнирами равных угловых скоростей. При этом внутренние шарниры обеспечивают вертикальное перемещение управляемых колес, а наружные шарниры – их поворот. Иногда (рис. 6.9, г) используют карданные передачи с двумя шарнирами неравных угловых скоростей 7 и одним шарниром равных угловых скоростей 4.
На рис. 6.10 приведена конструкция переднего моста автомобиля ВАЗ, имеющего привод на все колеса. Такой мост выполняет функции ведущего и управляемого мостов и имеет постоянный привод от раздаточной коробки. Картер моста 4 выполнен неразъемным из алюминиевого сплава. Внутри установлены главная передача 8 и дифференциал 7.
Картер моста крепится к кронштейну двигателя с помощью шпилек 3 и кронштейна 6. Привод передних колес осуществляется через карданную передачу.
Расчет мостов
Расчет балок мостов производится на прочность при режимах нагружения:
• прямолинейное движение с максимальной продольной силой и отсутствии действия поперечной силы;
• при полном заносе автомобиля с действием поперечной силы и отсутствии действия продольных сил;
• при переезде препятствия и динамическим нагружением вертикальной силой.
Схема расчета балки ведущего моста по первому и второму нагрузочным режимам приведена приведена на рис 6.11.
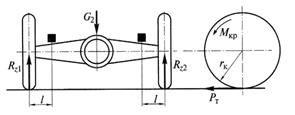
Рис. 6.11. Схемы нагружения балки ведущего моста: а – при прямолинейном движении и действии продольной силы PT; б – при боковом заносе и действии поперечной силы PY
При прямолинейном движении балка ведущего моста изгибается в вертикальной плоскости от действия сил Rz1 = Rz2 = 
где m2 = 1,2 – коэффициент динамического перераспределения нагрузки;
G2 – статическая нагрузка на мост;
φx = 0,9 – коэффициент сцепления колес с дорогой в продольном направлении.
Момент изгибающий в вертикальной плоскости:
момент изгибающий в горизонтальной плоскости:
где l – расстояние от линии действия силы до опасного сечения;
момент крутящий от действия касательной силы PT:
rк – радиус ведущего колеса.
В балке ведущего моста опасными сечениями являются сечения под площадками крепления рессор и места запрессовки полуосевых рукавов.
Результирующий момент изгиба и кручения в опасном сечении составит:
Mр = 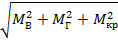
Для трубчатого круглого сечения результирующее напряжение
σр = 
где W = 0,2 
Для прямоугольного и коробчатого сечений напряжения изгиба в вертикальной и горизонтальной плоскостях определяются раздельно и суммируются арифметически:
σи = 
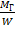
Поскольку напряжения изгиба относятся к переферийным волокнам, а напряжения кручения к средним волокнам, их определяют отдельно и с напряжением изгиба не суммируют:
τкр = 
где Wкр – момент сопротивления кручению сечения балки.
При расчетном режиме движения автомобиля с полным боковым заносом сила PT = 0 балка изгибается только в вертикальной плоскости под действием сил Rz и Ry. которые определяются зависимостями:
где φy – коэффициент сцепления колес с дорогой в поперечном направлении;
hц – высота расположения центра массы;
Изгибающие моменты от действия сил на левом и правом колесах:
Напряжение изгиба в опасном сечении балки:
σиз = 
Для расчетного режима переезда неровности балка моста изгибается от действия силы Rzkд. Напряжение изгиба в опасном сечении определится по формуле:
σиз = 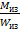

где kд – коэффициент динамичности: для легковых автомобилей kд = 1,75, для грузовых автомобилей kд = 2,5…3,0.
Допускаемые напряжения для расчета балок ведущих мостов составляют значения:
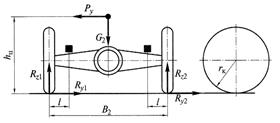
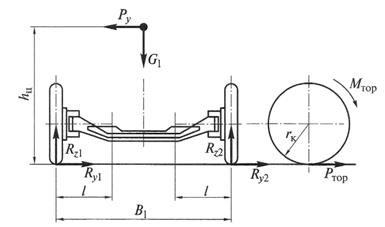
Балку управляемого моста(рис. 6.12)в режиме прямолинейного движения с торможением рассчитывают на прочность по напряжениям изгиба в вертикальной плоскости от действия сил Rz1 и Rz2 и в горизонтальной плоскости от действия силы Pтор. Кроме того на участке от поворотного кулака до опорной площадки под рессору балка испытывает напряжение кручения от действия тормозного момента на опорных щитах Мтор = Рторrк.
Рис. 6.12. асчетная схема балки управляемого моста
Изгибающий момент в вертикальной плоскости равен
изгибающий момент в горизонтальной плоскости
где l – плече изгибающей силы (рис. 6.12);
φx = 0,9 – коэффициент сцепления колеса с дорогой в продольном направлении.
При расчете по режиму полного заноса нормальная реакция на левом колесе будет больше, чем на правом. Изгибающие моменты в сечениях балки слева справа определятся из зависимостей:
Mиз1 = 

где G1 – нагрузка на управляемый мост;
В1 – колея передних колес;
hц – высота центра массы автомобиля.
При расчете балки в режиме преодоления препятствия определяется изгибающий момент в вертикальной плоскости
Mв = 
Поскольку сечение балки управляемого моста двутавровое, то напряжения изгиба определяют в вертикальной и в горизонтальной плоскости, а затем их арифметически складывают:
σ∑ = 

напряжение кручения определяется из соотношения:
τкр = 
где Wв и Wг – моменты сопротивления изгибу двутаврового сечения балки в вертикальной и горизонтальной плоскостях соответственно;
Wкр – момент сопротивления изгибу сечения балки.
Балки управляемых мостов изготавливают кованными из сталей марок 45, 30Х, 40Х.
Допускаемые напряжения изгиба [σиз] = 300МПа, допускаемое напряжение кручения [τкр] = 150МПа.
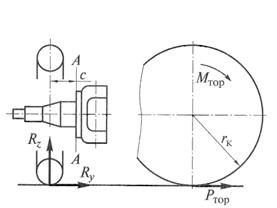
Расчет поворотных кулаков(рис. 6.13) ведется на изгиб в режиме торможения в вертикальной и горизонтальной плоскостях с проверкой сечения на переходе от цапфы к проушине. Изгибающий момент равен:
Mиз = с 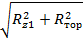
где с – плечо действия изгибающих сил.
Напряжение изгиба σиз = 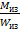
Рис. 6.13. Расчетная схема поворотного кулака
Напряжение изгиба цапфы поворотных кулаков в режиме заноса определим из соотношений:
σиз1 = 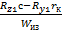

Напряжение изгиба цапфы поворотных кулаков в режиме преодоления препятствия
σиз = 
где с – плечо изгибающей силы.
Поворотные цапфы изготавливают из сталей марок 30Х, 40Х.
Допускаемые напряжения изгиба [σиз] = 300МПа.
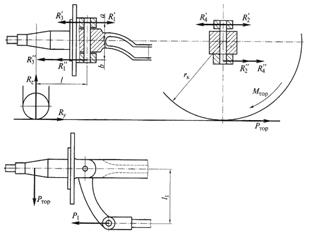
Расчет поворотных шкворней (рис. 6.14) ведется по тем же трем нагрузочным режимам с допущением, что ось шкворня располагается вертикально. Нагрузке подвергаются
Рис. 6.14. Расчетная схема поворотного шкворня
верхний и нижний концы шкворня.
В режиме торможения значение этих сил определится соотношениями:


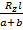
от действия тормозной силы –



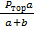
от действия реактивной силы P1 –


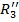

где Р1 = 
от действия тормозного момента Mтор = Рторrк –


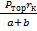
Суммарная сила, действующая на верхний конец шкворня, определится из радикала:


Суммарная сила, действующая на нижний конец шкворня, определится из радикала:


Из сравнения (6.23) и (6.24) следует, что нижний конец шкворня нагружен большей силой, чем верхний.
В режиме заноса автомобиля на верхний и нижний конец шкворня действуют силы:
от нормальной реакции Rz:




от действия поперечной силы Ry:










Здесь Rz1, Rz2, Ry1, Ry2 – нормальные и поперечные реакции на левом и правом колесе соответственно; 
При переезде через неровность дороги на шкворень действуют силы:


Шкворень на всех режимах рассчитывают на изгиб в опасном сечении, расположенном на границе с проушиной балки и срез, а втулки шкворня на смятие:
σиз = 

где h – высота проушины поворотного кулака;
d – диаметр сечения шкворня;
τср = 4 
σсм = 
Шкворни изготавливают из сталей марок 45, 50, 20Х, 20ХН, 18ХГТ. Допускаемые напряжения изгиба [σиз] = 500МПа, среза [τср] = 100Мпа, смятия [σсм] = 50МПа.