Перемещение автомобиля изображено на рисунке 3 определите координаты точки а

Материальная точка. Система отсчета. Перемещение. Определение координаты

Решебник к сборнику задач по физике для 7- 9 классов, Перышкин А.В.

1404. Можно ли считать автомобиль материальной точкой при определении пути, который он проехал за 2 ч? за 2 с?
В первом случае можно. Во втором случае нельзя, потому что тело можно считать материальной точкой тогда, когда его размеры меньше расстояний, рассматриваемых в задаче.

1405. Можно ли рассматривать поезд длиной 200 м как материальную точку при определении времени, за которое он проехал расстояние 2 м?
Нельзя. Длина поезда больше пройденного им расстояния. Для рассмотрения поезда в качестве материальной точки расстояние, пройденное им, должно быть больше его собственной длины.

1406. Можно ли считать поезд длиной 200 м материальной точкой при определении времени, за которое он проехал мост длиной 800 м?
Можно.

1407. Муха ползет по краю блюдца из точки А в точку В (рис. 176). На рисунке покажите:
а) траекторию движения мухи;
б) перемещение мухи.

1408. При каком движении материальной точки путь, пройденный точкой, равен модулю перемещения?
При прямолинейном.

1409. Рота солдат прошла на север 4 км, затем солдаты повернули на восток и прошли еще 3 км. Найдите путь и перемещение солдат за все время движения. Нарисуйте в тетради траекторию их движения.

1410. Найдите координаты точек А, В и С в системе координат XOY (рис. 177). Определите расстояния между точками:
а) А и В, б) В и С, в) А и С.

1411. На рисунке 178 показаны перемещения трех материальных точек: s1, s2, s3. Найдите:
а) координаты начального положения каждой точки;
б) координаты конечного положения каждой точки;
в) проекции перемещения каждой точки на координатную ось OX;
г) проекции перемещения каждой точки на координатную ось OY;
д) модуль перемещения каждой точки.

1413. Определите координаты пересечения траекторий двух муравьев А и В, которые движутся по траекториям, показанным на рисунке 179. При каком условии возможна встреча муравьев А и В?

1415. Мяч с расстояния h0 = 0,8 м от поверхности земли подбрасывают вертикально вверх на высоту h1 = 2,8 м от поверхности земли, затем мяч падает на землю. Нарисуйте координатную ось OX, направленную вертикально вверх с началом координат на поверхности земли. Покажите на рисунке:
а) координату x0 начального положения мяча;
б) координату xm максимального подъема мяча;
в) проекцию перемещения sx мяча за время полета.

1416. Решите предыдущую задачу, расположив начало координат в точке бросания мяча.

Источник

Перемещение автомобиля изображено на рисунке 3 определите координаты точки а

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Типовая задача «Уравнение координаты (нахождение неизвестной величины)»

Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»

Задача № 2. Движение двух тел задано уравнениями x₁ = 20 – 8t и х₂ = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»

Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.

Типовая задача «График координаты. Движение нескольких тел»

Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.

ЗАДАЧИ ПОСЛОЖНЕЕ

Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ:

РЕШЕНИЕ:

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.

Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.

Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.

При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.

В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:

Источник

Перемещение автомобиля изображено на рисунке 3 определите координаты точки а

Школьник летом на даче жил недалеко от военного аэродрома, на который постоянно садились военно-транспортные самолеты, которые летели всегда по одной и той же траектории («глиссаде»), проекция которой на землю являлась прямой линией, отстоящей на расстояние от дачи школьника. Он вооружился секундомером и точным угломерным инструментом, провел многократные измерения некоторых времен и углов и усреднил их для однотипных марок самолетов. Оказалось, что когда самолет находился на минимальном расстоянии от школьника, угол между горизонталью и направлением на самолет составлял а а звук его двигателей был слышен в месте нахождения школьника спустя время За это время самолет успевал удалиться от точки максимального сближения со школьником на угловое расстояние Исходя из этих данных, школьник определил скорость самолета. Чему она оказалась равна?

Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Обоснование. Движение самолета является поступательным, поэтому самолет можно считать материальной точкой и рассматривать перемещение в вертикальной плоскости. Учитывая, что промежуток времени очень мал, можно считать за данный интервал времени движение самолета прямолинейным и равномерным и применять законы данного вида движения.

Перейдем к решению. Поскольку угол наклона глиссады мал, то в момент максимального сближения самолета и школьника расстояние между ними примерно равно

где l — раcстояние до глиссады.

Звук от двигателей, излученный в этот момент, доходит до школьника, согласно условию, спустя время и школьник слышит максимум громкости.

За время t самолёт успевает удалиться от точки максимального сближения со школьником в направлении перпендикулярном L на расстояние, равное Таким образом, и скорость самолета

Источник

Перемещение автомобиля изображено на рисунке 3 определите координаты точки а

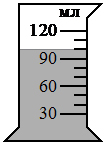
По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале времени от 0 до 2 с автомобиль прошёл путь

Примечание. В принципе, интересующий нас участок (от 0 до 2 с) не обязательно разбивать на два, площадь под графиком можно посчитать, как площадь трапеции:

В принципе, можно использовать стандартные кинематические формулы для изменения координаты, скорости, ускорения, а все необходимые данные снимать с графика. Но так получается значительно дольше.

Почему же не через площадь дольше?

S= So + vt + (at^2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;

Правильно. Так тоже можно.

В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.

В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂

Утверждение «в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)» не совсем верно, правильно тогда уж говорить так: «за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с».

Однако такое утверждение в свою очередь требует разъяснений.

так путь же нужно найти почему нельзя воспользоваться формулой S=Vt

Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется

В задании не сказано, но тело двигалось прямолинейно

Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.

На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Источник

ЕГЭ по физике: разбираем задания с учителем

Задание 1

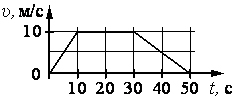
На рисунке представлен график зависимости модуля скорости от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 10 до 30 с.

Ответ: ____________________ м.

Решение

Путь, пройденный автомобилем в интервале времени от 10 до 30 с проще всего определить как площадь прямоугольника, сторонами которого являются, интервал времени (30 – 10) = 20 c и скорость v = 10 м/с, т.е. S = 20 · 10 м/с = 200 м.

Задание 2

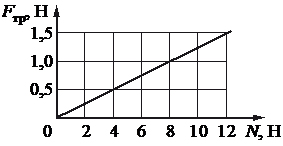
На графике приведена зависимость модуля силы трения скольжения от модуля силы нормального давления. Каков коэффициент трения?

Решение

На графике найдем точку, для которой можно точно определить координаты. Это в нашем случае может быть F_тр = 1,0 Н, N = 8 Н, тогда

Задание 3

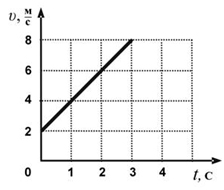
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости модуля скорости тела от времени. Какую мощность развивает эта сила в момент времени t = 3 c?

Решение

Для определения мощности силы по графику определим чему равен модуль скорости в момент времени 3 с. Скорость равна 8 м/с. Используем формулу для расчета мощности в данный момент времени: N = F · v (1), подставим числовые значения. N = 2 Н · 8 м/с = 16 Вт.

Задание 4

Деревянный шарик ( ρ _ш = 600 кг/м 3 ) плавает в растительном масле ( ρ _м = 900 кг/м 3 ). Как изменится выталкивающая сила, действующая на шар и объем части шара, погруженной в жидкость если масло заменить на воду ( ρ _в = 1000 кг/м 3 )

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Выталкивающая сила, действующая на шарик

Объем части шарика, погруженной в жидкость

Решение

Так как плотность материала шарика ( ρ _ш = 600 кг/м 3 ) меньше плотности маслa ( ρ _м = 900 кг/м 3 ) и меньше плотности воды ( ρ _в = 1000 кг/м 3 ), то шар плавает и в масле и в воде. Условие плавания тела в жидкости заключается в том, что выталкивающая сила F a уравновешивает силу тяжести, то есть F _а = F_т. Так как сила тяжести шарика при замене масла на воду не изменилась, то не изменилась и выталкивающая сила.

Выталкивающую силу можно вычислить по формуле:

где V_пчт – объем погруженной части тела, ρ _ж – плотность жидкости, g – ускорение свободного падения.

Выталкивающие силы в воде и в масле равны.

Плотность масла меньше плотности воды, следовательно, чтобы выполнялось равенство (2) необходимо, чтобы объем части шарика, погруженной в масло V_мпчт, был больше объема части шарика, погруженной в воду V_впчт. Значит при замене масла на воду, объем части шарика, погруженной в воду уменьшается.

Выталкивающая сила, действующая на шарик

Объем части шарика, погруженной в жидкость

Задание 5

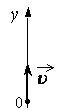
Шарик брошен вертикально вверх с начальной скоростью 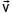(см. рисунок). Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять (t₀ – время полета). К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ГРАФИКИ

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

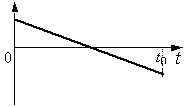
проекция скорости шарика

проекция ускорения шарика

модуль силы тяжести, действующей на шарик

Решение

Определим по условию задачи характер движения шарика. Учитывая, что шарик движется с ускорением свободного падения, вектор которого направлен противоположно выбранной оси, уравнение зависимости проекции скорости от времени, будет иметь вид: v_1y = v_y – gt (1) Скорость шарика уменьшается, и в наивысшей точке подъема равна нулю. После чего шарик начнет падать до момента t₀ – всего времени полета. По величине скорость шарика в момент падения будет равна v, но проекция вектора скорости будет отрицательна, так как направление оси y и вектора скорости противоположны. Следовательно график по буквой А, соответствует зависимости по номером 2) проекции скорости от времени. Графику под буквой Б) соответствует зависимость под цифрой 3) проекция ускорения шарика. Так как ускорение свободного падения у поверхности Земли можно считать постоянным, то графиком будет прямая линия, параллельная оси времени. Так как вектор ускорения и направление не совпадают по направлению, то проекция вектора ускорения отрицательная.

Полезно исключить ответы неверные. Если движение равнопеременное, то графиком зависимости координаты от времени, должна быть парабола. Такого графика нет. Модуль силы тяжести, этой зависимости должен соответствовать график расположенный выше оси времени.

Задание 6

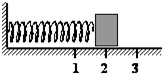
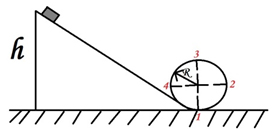
Груз изображенного на рисунке пружинного маятника совершает гармонические колебания между точками 1 и 3. Как меняется кинетическая энергия груза маятника, скорость груза и жесткость пружины при движении груза маятника от точки 2 к точке 1

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Кинетическая энергия груза

Решение

Груз на пружине совершает гармонические колебания между точками 1 и 3. Точка 2 соответствует положению равновесия. Согласно закону сохранения и превращения механической энергии при переходе груза из точки 2 к точке 1, энергия не исчезает, она превращается из одного вида в другой. Полная энергия сохраняется. В нашем случае увеличивается деформация пружины, возникающая сила упругости будет направлена к положению равновесия. Поскольку сила упругости направлена против скорости движения тела, то она тормозит его движение. Следовательно, скорость шарика уменьшается. Кинетическая энергия уменьшается. Увеличивается потенциальная энергия. Жесткость пружины в ходе движения тела не изменяется.

Кинетическая энергия груза

Задание 7

Установите соответствие между зависимостью координаты тела от времени (все величины выражены в СИ) и зависимостью проекции скорости от времени для того же тела. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами

КООРДИНАТА

СКОРОСТЬ

Решение

Полезно записать закон движения (зависимость координаты тела от времени) в общем виде:

где х₀ – начальная координата тела; v_x – проекция вектора скорости на выбранную ось; a _x – проекция вектора ускорения на выбранную ось; t – время движения.

Для нашего случая vx = 4t – 5.

Задание 8

В результате нагревания неона абсолютная температура газа увеличилась в 4 раза. Во сколько раз изменилась при этом средняя кинетическая энергия теплового движения его молекул?

Решение

Необходимо вспомнить связь средней кинетической энергии теплового движения молекул и температуры.

где k – постоянная Больцмана, T – температура газа в Кельвинах. Из формулы видно, что зависимость средней кинетической энергии от температуры прямая, то есть во сколько раз изменяется температура, во столько раз изменяется средняя кинетическая энергия теплового движения молекул.

Задание 9

Газ в некотором процессе отдал количество теплоты 35 Дж, а внутренняя энергия газа в этом процессе, увеличилась на 10 Дж. Какую работу совершили над газом внешние силы?

Решение

В условии задачи идет речь о работе внешних сил над газом. Поэтому первый закон термодинамики лучше записать в виде:

Где ∆U = 10 Дж – изменение внутренней энергии газа; Q = –35 Дж – количество теплоты отданное газом, A_в.с – работа внешних сил.

Подставим числовые значения в формулу (1) 10 = –35 + А_в.с; Следовательно работа внешних сил будет равна 45 Дж.

Задание 10

Парциальное давление водяных паров при 19° С было равно 1,1 кПа Найти относительную влажность воздуха, если давление насыщенного пара при этой температуре равно 2,2 кПа?

Решение

По определению относительной влажности воздуха

φ – относительная влажность воздуха, в процентах; P_в.п – парциальное давление водяного пара, P_н.п – давление насыщенного пара при данной температуре.

Подставим числовые значения в формулу (1).

Задание 11

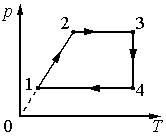
Изменение состояния фиксированного количества одноатомного идеального газа происходит по циклу, показанному на рисунке.

Установите соответствие между процессами и физическими величинами (∆U – изменение внутренней энергии; А – работа газа), которые их характеризуют.

К каждой позиции из первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры по соответствующими буквами.

ПРОЦЕССЫ

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

Решение

Данный график можно перестроить в осях PV или разобраться с тем, что дано. На участке 1–2, изохорный процесс V = const; Растет давление и температура. Газ работу не совершает. Поэтому A = 0, Изменение внутренней энергии больше нуля. Следовательно, верно записаны физические величины и их изменения под номером 4) ΔU > 0; A = 0. Участок 2–3: изобарный процесс, P = const; увеличивается температура и увеличивается объем. Газ расширяется, работа газа A>0, Следовательно, переходу 2–3 соответствует запись под номером 1) ΔU > 0; A > 0.

Задание 12

Идеальный одноатомный газ, находящийся в цилиндре под тяжелым поршнем (трением между поверхностью поршня и цилиндром можно пренебречь), медленно нагревают от 300 К до 400 К. Внешнее давление при этом не изменяется. Затем этот же газ вновь нагревают от 400 К до 500 К, но уже с закрепленным поршнем (поршень не двигается).

Сравните работу газа, изменение внутренней энергии и количество теплоты, полученное газом, в первом и втором процессах.

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Изменение внутренней энергии

Количество теплоты, полученное газом

Решение

Если газ медленно нагревают в цилиндре с незакрепленным тяжелым поршнем, то при неизменном внешнем давлении процесс можно считать изобарным (давление газа не изменяется)

Следовательно, работу газа можно вычислить по формуле:

где A – работа газа в изобарном процессе; P – давление газа; V₁ – объем газа в начальном состоянии; V₂ – объем газа в конечном состоянии.

Изменение внутренней энергии идеального одноатомного газа вычисляется по формуле:

где v – количество вещества; R – универсальная газовая постоянная; ∆T – изменение температуры газа.

По первому закону термодинамики количество теплоты, полученное газом, равно

Если газ нагревают в цилиндре с закрепленным поршнем, то процесс можно считать изохорным (объем газа не изменяется). В изохорном процессе идеальный газ не совершает работу (поршень не перемещается).

Изменение внутренней энергии равно:

Количество теплоты в этом случае: Q = 150 v R (7)

Сравнивая (1) и (5), (2) и (6), (4) и (7) делаем вывод. Работа газа уменьшилась, Изменение внутренней энергии осталось прежним, количество теплоты, полученное газом, уменьшилось.

Изменение внутренней энергии

Количество теплоты, полученное газом

Задание 13

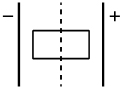
В электрическое поле внесли незаряженный кусок диэлектрика (см. рисунок). Затем его разделили на две равные части (пунктирная линия) и после этого вынесли из электрического поля. Какой заряд будет иметь каждая часть диэлектрика?

Решение

Если внести в электрическое поле диэлектрик, (вещество в котором нет свободных электрических зарядов) при обычных условиях, то наблюдается явление поляризации. В диэлектриках заряженные частицы не способны двигаться по всему объему, а могут лишь смещаться на небольшие расстояния относительно своих постоянных положений, электрические заряды в диэлектриках связанные. Если диэлектрик вынести из поля, то заряд обеих частей равен нулю.

Задание 14

Колебательный контур состоит из конденсатора емкостью C и катушки с индуктивности L. Как изменится частота и длина волны колебательного контура, если площадь пластин конденсатора уменьшить в два раза? Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Решение

В задаче говорится о колебательном контуре. По определению периода колебаний возникающих в контуре 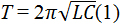, длина волны связана с частотой

где v – частота колебаний. По определению емкости конденсатора

где ε ₀ – электрическая постоянная, ε – диэлектрическая проницаемость среды. По условию задачи уменьшают площадь пластин. Следовательно, уменьшается емкость конденсатора. Из формулы (1) видим, что уменьшится период электромагнитных колебаний, возникающих в контуре. Зная связь периода и частоты колебаний

видим, что частота колебаний увеличивается. А используя формулу (2), заключаем, что длина волны уменьшается.

Задание 15

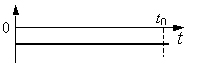
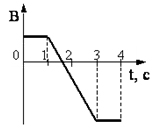
На графике показано как меняется индукция магнитного поля с течением времени в проводящем контуре. В какой промежуток времени в контуре будет возникать индукционный ток.

Решение

По определению индукционный ток в проводящем замкнутом контуре возникает при условии изменения магнитного потока, пронизывающего этот контур.

Закон электромагнитной индукции, где Ɛ – ЭДС индукции, ∆ Φ – изменение магнитного потока, ∆t промежуток времени, в течении которого происходят изменения.

Магнитный поток по условию задачи будет меняться, если меняется индукция магнитного поля. Это происходит в интервале времени от 1 с до 3 с. Площадь контура не изменяется. Следовательно, индукционный ток возникает в случае

Задание 16

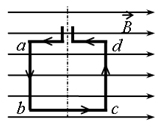
Квадратная рамка расположена в однородном магнитном поле в плоскости линий магнитной индукции (см. рисунок). Направление тока в рамке показано стрелками. Как направлена сила, действующая на сторону ab рамки со стороны внешнего магнитного поля 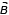? (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя)

Решение

На рамку с током со стороны магнитного поля действует сила Ампера. Направление вектора силы Ампера определяется мнемоническим правилом левой руки. Четыре пальца левой руки направляем по току стороны ab, вектор индукции В, должен входить в ладонь, тогда большой палец покажет направление вектора силы Ампера.

Ответ: к наблюдателю.

Задание 17

Заряженная частица влетает с некоторой скоростью в однородное магнитное поле перпендикулярно силовым линиям поля. С некоторого момента времени, модуль индукции магнитного поля увеличили. Заряд частицы не изменился.

Как изменилась сила, действующая на движущуюся частицу в магнитном поле, радиус окружности, по которой движется частица, и кинетическая энергия частицы после увеличения модуля индукции магнитного поля?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Радиус окружности, по которой движется частица

Кинетическая энергия частицы

Решение

На частицу, движущуюся в магнитном поле, действует со стороны магнитного поля сила Лоренца. Модуль силы Лоренца можно рассчитать по формуле:

где B – индукция магнитного поля, q – заряд частицы, v – скорость частицы, α – угол, между вектором скорости и вектором магнитной индукции.

где m – масса частицы. Следовательно, с увеличением индукции поля, радиус окружности уменьшается.

Сила Лоренца работы не совершает над движущейся частицей, так как угол между вектором силы и вектором перемещения (вектор перемещения направлен по вектору скорости) равен 90°.

Поэтому кинетическая энергия независимо от значения индукции магнитного поля не изменяется.

Радиус окружности, по которой движется частица

Кинетическая энергия частицы

Задание 18

А) Мощность тока, выделяющаяся на резисторе

Б) Напряжение на резисторе

3)

4)

Решение

Полезно вспомнить, как рассчитывается мощность электрического тока.

где P – мощность электрического тока, A – работа электрического тока, t – время, в течение которого по проводнику протекает электрический ток. Работа, в свою очередь, рассчитывается

где I – сила электрического тока, U – напряжение на участке,

Задание 19

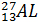В результате реакции ядра и α частицы появились протон и ядро: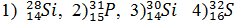

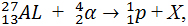
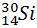
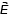Решение

Pапишем ядерную реакцию для нашего случая:

В результате этой реакции, выполняется закон сохранения зарядового и массового числа. Z = 13 + 2 – 1 = 14; M = 27 + 4 – 1 = 30.

Следовательно, ядро под номером 3)

Задание 20

Период полураспада вещества составляет 18 минут, первоначальная масса 120 мг, Чему будет равна масса вещества через 54 минуты, ответ выразить в мг?

Решение

Задача на использование закона радиоактивного распада. Его можно записать в виде

Задание 21

Фотокатод фотоэлемента освещают ультрафиолетовым светом определенной частоты. Как изменяется работа выхода материала (вещества) фотокатода, максимальная кинетическая энергия фотоэлектронов и красная граница фотоэффекта, если частоту света увеличить?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода материала фотокатода

Максимальная кинетическая энергия фотоэлектронов

Красная граница фотоэффекта

Решение

Полезно вспомнить определение фотоэффекта. Это явление взаимодействия света с веществом, в результате которого энергия фотонов передается электронам вещества. Различают внешний и внутренний фотоэффект. В нашем случае речь идет о внешнем фотоэффекте. Когда под действием света происходит вырывание электронов из вещества. Работа выхода зависит от материала, из которого изготовлен фотокатод фотоэлемента, и не зависит от частоты света. Поэтому при увеличении частоты ультрафиолетового света, падающего на фотокатод, работа выходане изменяется.

Запишем уравнение Эйнштейна для фотоэффекта:

hv – энергия фотона, падающего на фотокатод, A_вых – работа выхода, E_к – максимальная кинетическая энергия фотоэлектронов, вылетающих из фотокатода под действием света.

Из формулы (1) выразим

следовательно, при увеличении частоты ультрафиолетового света максимальная кинетическая энергия фотоэлектронов увеличивается.

это минимальная частота, при которой еще возможен фотоэффект. Так как работа выхода не изменяется, то и красная граница фотоэффекта для нашего материала не изменяется.

Работа выхода материала фотокатода

Максимальная кинетическая энергия фотоэлектронов

Красная граница фотоэффекта

Задание 22

В мензурку налита вода. Выберите верное значение объема воды, учитывая, что погрешность измерения равна половине цены деления шкалы.

Решение

Задание проверяет умение записывать показания измерительного прибора с учетом заданной погрешности измерений. Определим цену деления шкалы

Погрешность измерения по условию равна половине цены деления, т.е.

Конечный результат запишем в виде:

Задание 23

Проводники изготовлены из одного и того же материала. Какую пару проводников нужно выбрать, чтобы на опыте обнаружить зависимость сопротивления проволоки от ее диаметра?

Решение

В задание говорится о том, что проводники изготовлены из одного и того же материала, т.е. их удельные сопротивления одинаковые. Вспомним от каких величин зависит сопротивление проводника и запишем формулу для расчета сопротивления:

где R – сопротивление проводника, p – удельное сопротивление материал, l – длина проводника, S – площадь поперечного сечения проводника. Для того, чтобы выявить зависимость проводника от диаметра нужно взять проводники одинаковой длины, но разного диаметра. Заем, что площадь поперечного сечения проводника определяется как площадь круга:

где d – диаметра проводника. Следовательно, вариант ответа: 3.

Задание 24

Снаряд массой 40 кг, летящий в горизонтальном направлении со скоростью 600 м/с, разрывается на две части массами 30 кг и 10 кг. Большая часть движется в прежнем направлении со скоростью 900 м/с. Определите числовое значение, и направление скорости меньшей части снаряда. В ответ запишите модуль этой скорости.

m = m₁₁ + m₂₂ (1)

Выберем положительное направление оси Х, совпадающей с направлением скорости снаряда, тогда в проекции на эту ось уравнение (1) запишем:

Выразим из формулы (2) проекцию вектора скорости второго осколка.

подставим числовые значения.

Меньшая часть снаряда в момент разрыва имеет скорость 300 м/с, направленную в сторону, противоположную первоначальному движению снаряда.

Задание 25

В калориметре находятся в тепловом равновесии 50 г воды и 5 г льда. Какой должна быть минимальная масса болта, имеющего удельную теплоемкость 500 Дж/кг К и температуру 339 К, чтобы после опускания его в калориметр весь лед растаял? Тепловыми потерями пренебречь. Ответ представить в граммах.

Решение

Для решения задачи важно вспомнить уравнение теплового баланса. Если потерь нет, то в системе тел происходит теплопередача энергии. В результате чего, лед плавиться. Первоначально вода и лед находились в тепловом равновесии. Это значит, что начальная температура была 0° С или 273 К. Помним перевод из градусов Цельсия в градусы Кельвина. Т = t + 273. Так как по условию задачи спрашивается о минимальной массе болта, то энергии должно хватить только, чтобы расплавить лед.

где λ – удельная теплота плавления, m_л – масса льда, m_б – масса болта.

Выразим из формулы (1)

Задание 26

В цепи, показанной на рисунке, идеальный амперметр показывает 6 А. Найдите ЭДС источника, если его внутреннее сопротивление 2 Ом.

Решение

Внимательно читаем условие задачи и разбираемся со схемой. В ней есть один элемент, который можно не заметить. Это пустой провод между резисторами в 1 Ом и 3 Ом. Если цепь будет замкнута, то электрический ток пройдет по этому проводу с наименьшим сопротивлением и через резистор 5 Ом.

Тогда закон Ома для полной цепи запишем в виде:

где – сила тока в цепи, ε – ЭДС источника, R – сопротивление нагрузки, r – внутренне сопротивление. Из формулы (1) выразим ЭДС

ε = 6 A (5 Ом + 2 Ом) = 42 В.

Задание 27

В камере, из которой откачали воздух, создали электрическое поле напряженностью и магнитное поле с индукцией . Поля однородные и векторы взаимно перпендикулярны. В камеру влетает протон p, вектор скорости которого перпендикулярен вектору напряженности и вектору магнитной индукции. Модули напряженности электрического поля и индукции магнитного поля таковы, что протон движется прямолинейно. Объясните, как изменится начальный участок траектории протона, если индукции магнитного поля увеличить. В ответе укажите, какие явления и закономерности Вы использовали для объяснения. Влиянием силы тяжести пренебречь.

Решение

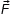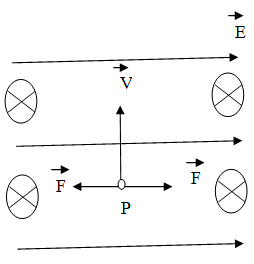
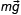В решении задачи необходимо остановиться на первоначальном движении протона и на изменении характера движения после изменения индукции магнитного поля. На протон действует магнитное поле силой Лоренца, модуль которой равен F_л = qvB и электрическое поле силой, модуль которой равен F_э = qE. Поскольку заряд протона положительный, то _э сонаправлена с вектором напряженности электрического поля. (См. рисунок) Так как протон первоначально двигался прямолинейно, то по модулю эти силы были равны согласно второму закону Ньютона.

С увеличением индукции магнитного поля будет увеличиваться сила Лоренца. Равнодействующая сил в этом случае будет отлична от нуля и направлена в сторону большей силы. А именно в сторону силы Лоренца. Равнодействующая сила сообщает протону ускорение, направленное влево, траектория протона будет криволинейной, отклоняющейся от первоначального направления.

Задание 28

Тело соскальзывает без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. С какой высоты тело должно начать движение, чтобы не оторваться от желоба в верхней точке траектории.

Решение

Нам дана задача о неравномерно переменном движении тела по окружности. В процессе этого движения изменяется положение тела по высоте. Проще решить задачу, используя уравнения закона сохранения энергии и уравнения второго закона Ньютона по нормали к траектории движения. Сделали рисунок. Запишем формулу закона сохранения энергии:

где W₂ и W₁ – полная механическая энергия в первом и втором положении. За нулевой уровень выберем положение стола. Нас интересуют два положения тела – это положение тела в начальный момент движения, второе – положение тела в верхней точке траектории (это точка 3 на рисунке). В процессе движения на тело действуют две силы: сила тяжести = и сила реакции опоры 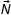. Работа силы тяжести учитывается в изменении потенциальной энергии, сила работу не совершает, так она всюду перпендикулярна перемещению. А = 0 (2)

В положении 2 (точка 3 на рисунке):

где v – скорость тела в точке 3. Подставляя полученные выражения в формулу (1), получим

В верхней точке петли на тело действует две силы , по второму закону Ньютона

При уменьшении начальной высоты спуска скорость шарика в верхней точке петли уменьшается и при некотором значении h становится такой, что он пролетает верхнюю точку петли, лишь касаясь желоба. Для этого предельного случая N = 0 и уравнение второго закона примет вид:

Решая уравнения (5) и (7) получим h = 2,5 R

Задание 29

Воздух в комнате объемом V = 50 м 3 имеет температуру t = 27° C и относительную влажность воздуха φ ₁ = 30%. Сколько времени τ должен работать увлажнитель воздуха, распыляющий воду с производительностью μ = 2 кг/ч, чтобы относительная влажность в комнате повысилась до φ ₂ = 70%. Давление насыщенных паров воды при t = 27° C равно p_н = 3665 Па. Молярная масса воды 18 г/моль.

Решение

Приступая к решению задач на пары и влажность, всегда полезно иметь в виду следующее: Если задана температура и давление (плотность) насыщающего пара, то его плотность (давление) определяют из уравнения Менделеева-Клапейрона. Записать уравнение Менделеева-Клапейрона и формулу относительной влажности для каждого состояния.

Для первого случая при φ ₁ = 30% парциальное давление водяного пара выразим из формулы:

Запишем уравнение Менделеева – Клапейрона

где T = t + 273 (К), R – универсальная газовая постоянная. Выразим начальную массу пара, содержащегося в комнате используя уравнение (2) и (3):

аналогично при влажности φ ₂ масса пара

Время, которое должен работать увлажнитель воздуха, можно рассчитать по формуле

подставим (4) и (5) в (6)

Подставим числовые значения и получим, что увлажнитель должен работать 15,5 мин.

Задание 30

Определите ЭДС источника, если при подключении к нему резистора с сопротивлением R напряжение на зажимах источника U₁ = 10 B, а при подключении резистора 5R напряжение U₂ = 20 B.

Решение

Запишем уравнения для двух случаев.

где r – внутреннее сопротивление источника, Ɛ – ЭДС источника.

где U₁ и U₂ – напряжение на зажимах в первом и втором случае.

Учитывая закон Ома для участка цепи, перепишем уравнения (1) и (3) в виде:

Из уравнения (6) выразим внутреннее сопротивление и подставим в (5)

Последняя подстановка для расчета ЭДС. Формулу (7) подставим в (5)

Задание 31

При освещении пластинки изготовленной из некоторого материала, светом с частотой v ₁ = 8 · 1014 Гц, а затем v ₂ = 6 · 1014 Гц обнаружилось, что максимальная кинетическая энергия электронов изменилась в 3 раза. Определите работу выхода электронов из этого металла.

Решение

Если частота кванта света, вызывающего фотоэффект, уменьшается, то уменьшается и кинетическая энергия. Поэтому кинетическая энергия во втором случае тоже будет меньше в три раза. Запишем уравнение Эйнштейна для фотоэффекта для двух случаев.

для первой частоты света

для второй частоты света

Решаем уравнения (1) и (2) совместно. Вычтем из (1) (2) и выразим Е_к

формула для кинетической энергии.

Из уравнения (1) выразим работу выхода и подставим вместо кинетической энергии выражение (3)

Источник