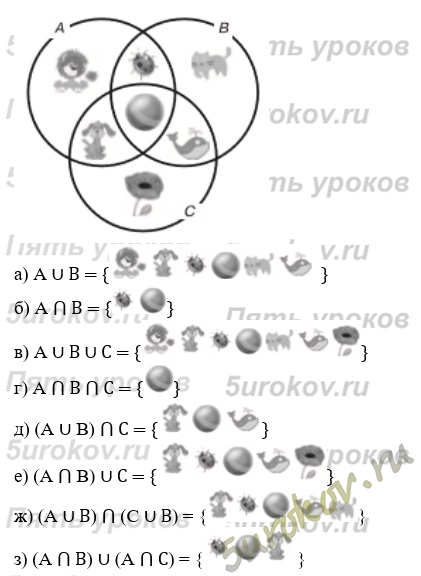
Проанализируй и выбери верный ответ пусть а множество автомобилей в множество volvo
Урок 4
Разнообразие отношений объектов и их множеств
Отношения между множествами
Практическая работа №3
«Повторяем возможности графического редактора – инструмента создания графических объектов» (задания 1–3)
Содержание урока
Отношения объектов и их множеств. Отношения между множествами
Отношения объектов и их множеств. Отношения между множествами
Отношения могут связывать два множества объектов, например:
• «файлы группируются в папки»;
• «колеса входят в состав автомобилей»;
• «бабочки — это насекомые («являются разновидностью насекомых)».
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.
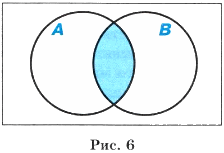
Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и Б, то говорят, что эти множества пересекаются (рис. 6).
Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.
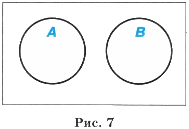
Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7)
Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.
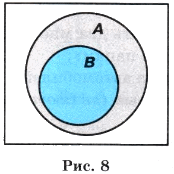
Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).
Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.
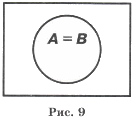
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).
Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.
Следующая страница 
Cкачать материалы урока
Отношения между множествами
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.
Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются (рис. 6).
Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.
Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7).
Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.
Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).
Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).
Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.
Проанализируй и выбери верный ответ пусть а множество автомобилей в множество volvo
Общение людей – это чередование вопросов и ответов. Знания высказываются в форме суждений. Суждения – это некоторое высказывание, которое может быть истинным или ложным.
Частные – конкретные факты «2+3>3» или «сейчас идет дождь».
Общие – о свойстве группы объектов «х 2 ≥ 0», « любой квадрат – параллелограмм», они могут истинны для одних значений и ложны для других или тождественно истинными.
Часто в ответах на вопросы используются связки и, или, не. Изобразить это можно с помощью кругов Эйлера-Венна.
В этом случае вводятся обозначения А и В=А ∩ В, А или В=А ∪ В, не А=A, А/В= «А без В»
Пусть А= «множество красивых людей», а В= «множество умных людей»
Изобразим на схеме зеленым цветом множества А и В, А или В и другие.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 3. Отношения объектов и их множеств
Информатика. 6 класса. Босова Л.Л. Оглавление
Ключевые слова:
Разнообразие отношений.
Человек может рассказать не только о признаках объекта, но и об отношениях, в которых этот объект находится с другими объектами. Например:
В каждом из приведённых предложений выделено имя отношения, которое обозначает характер связи между двумя объектами.
Отношение — это взаимная связь, в которой находятся какие-либо объекты.
Одним и тем же отношением могут быть попарно связаны несколько объектов. Соответствующее словесное описание может оказаться очень длинным, и тогда в нём трудно разобраться.
Пусть про населённые пункты А, Б, В, Г, Д и Е известно, что некоторые из них соединены железной дорогой: населённый пункт А соединён железной дорогой с населёнными пунктами В, Г и Е, населённый пункт Е — с населёнными пунктами А, В, Г и Д.
Для большей наглядности имеющиеся связи («соединён железной дорогой») можно изобразить линиями на схеме отношений. Объекты на схеме отношений могут быть изображены кругами, овалами, точками, прямоугольниками и т. д. (рис. 4).
Имена некоторых отношений изменяются, когда меняются местами имена объектов, например: «выше» — «ниже», «приходится отцом» — «приходится сыном». В этом случае направление отношения на схеме отношений обозначают стрелкой.
Так, на рис. 4 каждая стрелка направлена от отца к его сыну и поэтому отражает отношение «приходится отцом», а не «приходится сыном». Например: «Андрей приходится отцом Ивану».
Стрелки можно не использовать, если удаётся сформулировать и соблюсти правило взаимного расположения объектов на схеме. Например, если на рис. 5 имена детей всегда располагать ниже имени их отца, то можно обойтись без стрелок.
Такие отношения, как «приходится сыном», «соединён железной дорогой», «покупает», «лечит» и т. д., могут связывать только объекты некоторых видов. В отношениях «является элементом множества», «входит в состав» и «является разновидностью» могут находиться любые объекты.
Отношения могут существовать не только между двумя объектами, но и между объектом и множеством объектов, например:
В каждом из этих предложений описано отношение «является элементом множества».
Отношения между множествами
Отношения могут связывать два множества объектов, например:
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.
Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются (рис. 6).
Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.
Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7).
Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.
Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).
Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.
Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).
Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.
Отношение «входит в состав»
В зависимости от ситуации объект может либо рассматриваться как единое целое, либо «распадаться» на более мелкие объекты. Например, компьютер рассматривается как единое целое, если нужно подсчитать количество компьютеров в школе. Чтобы получить представление о возможностях компьютера, необходимо рассмотреть характеристики таких его устройств, как процессор, память, жёсткий диск и т. д.
Объект может состоять из множества одинаковых (однородных, подобных) объектов. Например, объект «апельсин» состоит из частей — долек апельсина. Объект «школьный класс» состоит из множества учеников — мальчиков и девочек приблизительно одного возраста. Каждый ученик является целой, самостоятельной частью объекта «школьный класс».
Объект может состоять из множества различных объектов. Например, объект «компьютер» состоит из множества не похожих друг на друга объектов (системный блок, монитор, клавиатура и т. д.). При делении объекта «компьютер» на части новые объекты получают разные имена; признаки новых объектов различны.
При описании состава объектов в одних случаях речь идет о составе конкретного объекта, а в других — об общих составных частях множества объектов. В последнем случае описание состава содержит ответ на вопрос «Из чего обычно состоят объекты некоторого множества?». Например:
Описывая состав объекта, человек мысленно «разбирает» его на части. При этом, как правило, используют такой приём: сначала называют небольшое число крупных частей, затем каждую из них «разбирают» на части поменьше и т. д. Например, при описании состава дома удобно выделить сначала фундамент, стены и крышу, затем в составе стены выделить окно и дверь, затем сообщить, что окно состоит из рамы и стёкол, и так же поступить, описывая состав двери (рис. 10).
Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части. Таким образом, она отражает строение (структуру) объекта. На схеме состава можно использовать линии без стрелок, если имя объекта-части располагать ниже имени объекта, которому принадлежит эта часть.
Все имена на рис. 11 — общие (обозначают множества предметов), потому что эта схема отражает состав не одного конкретного дома, а «дома вообще».
При описании признаков сложного, составного объекта человек может назвать не только действия и характеристики всего объекта, но также действия и свойства объектов-частей. Например, весь дом можно строить и ремонтировать, крышу — красить, а стекло — вставлять; весь дом имеет длину, ширину и высоту, стены — толщину, крыша — высоту.
Самое главное
В сообщении об объекте могут быть приведены не только признаки данного объекта, но и отношения, которые связывают его с другими объектами. Имя отношения обозначает характер этой связи. Отношения могут связывать не только два объекта, но и объект с множеством объектов или два множества.
В зависимости от ситуации объект может рассматриваться как единое целое либо «распадаться» на более мелкие объекты.
Объект может состоять из множества одинаковых (однородных, подобных) объектов или множества различных объектов.
Схема отношений «входит в состав» (схема состава) отражает не только составные части, но и тот порядок, в котором предмет «разбирался» на части.
Проанализируй и выбери верный ответ пусть а множество автомобилей в множество volvo
Тест. 6 класс. Вариант 2. ОТНОШЕНИЯ ОБЪЕКТОВ И ИХ МНОЖЕСТВ. СИСТЕМА ОБЪЕКТОВ.
Какие выражения характеризуют отношение между множествами?
Вопрос 4
Выбери пример отношения является элементом множества.
Вопрос 5
Что такое круги Эйлера?
Вопрос 6
Пусть множество С-сказки, множество П-произведения А.С. Пушкина. Выбери пересечение множеств П и С.
Вопрос 7
В каком случае множество В является подмножеством множества А?
Вопрос 8
Что означает отношение:объект А входит в состав объекта В?
Вопрос 9
Пусть объект А-автомобиль, а объект В-двигатель. Можно ли сказать, что В входит в состав А?
Вопрос 10
Что такое подсистема?
Вопрос 11
Вопрос 12
Укажите ситуацию, в которой система не должна восприниматься как «чёрный ящик».
Вопрос 13
Подход к описанию сложного объекта, при котором не просто называют его составные части, но и рассматривают их взаимодействие и взаимовлияние, принято называть.
Ответы по параграфу 1.3 Элементы теории множеств и комбинаторики
Задание 2. Задайте путем перечисления всех элементов:
а) множество О всех цифр, используемых для записи чисел в восьмеричной системе счисления;
б) множество К всех цепочек из 0 и 1, состоящих ровно из трех символов.
Задание 4. Обсудите в группе и запишите с помощью фигурных скобок множества:
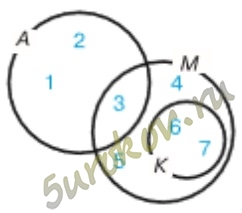
Задание 5. Из каких элементов состоит:
а) объединение К и М;
б) пересечение К и М;
в) дополнение К до М;
г) дополнение пересечения М и А до М?
а) K ∪ M =
б) K ⋂ M =
в) дополнение К до М =
г) дополнение (M ⋂ A = ) до М =
Задание 6. В классе 35 учеников. 20 – из них занимаются в математическом кружке, 11 – в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?
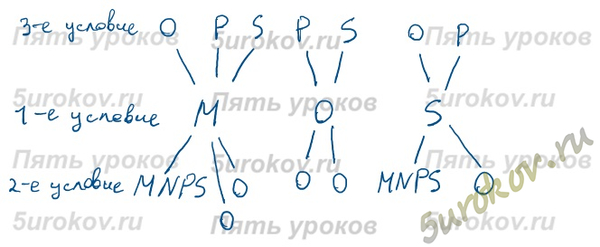
Задание 7. Для составления цепочек используются бусины, помеченные буквами: M, N, O, P, S. Сколько разных цепочек можно составить из трех бусин, для которых выполняются следующие условия:
1) в середине цепочки стоит одна из бусин M, O, S;
2) третья бусина – любая гласная, если первая буква согласная, и любая согласная, если первая буква гласная;
3) на первом месте – одна из бусин O, P, S, не стоящая в цепочке в середине?
Ответ: 13 различных цепочек.
По середине у нас бусины M, O, S (1-е условие), по 3-му условию на первом месте у нас бусины O, P, S, не стоящие в цепочке в середине.
Для М на первом месте могут быть O, P, S. Для O на первом месте могут быть P, S (O не может быть на первом месте, так как в середине уже стоит такая бусина). Для S на первом месте могут быть O, P.
Чтобы выбрать третью бусину, мы придерживаемся 2-му условию. Так у нас получится 13 вариантов цепочек.
Задание 8. Сколько существует способов составить слово «ВИРУС», начиная с буквы В и двигаясь вправо или вниз до последней буквы?
Задание 9. Алла Радугина защитила свой компьютер одним из четырехсимвольных паролей, составленных из букв «А» и «Р». Сколько всего существует вариантов таких паролей? Перечислите их.
Задание 10. Каждый пользователь некой компьютерной системы получает уникальный идентификатор, представляющий собой k-символьную цепочку в четырехбуквенном алфавите. Укажите наименьшее k, позволяющее зарегистрировать в системе не менее тысячи пользователей.
Задание 11. Иван разработал приложение для планшета и защитил его оригинальным графическим ключом, использовав в качестве узлов вершины пятиугольника (каждую из вершин надо задействовать ровно один раз). Прав ли Иван, утверждая, что количество комбинаций его графического ключа ничуть не меньше, чем количество вариантов трехзначного цифрового пароля, вводимого со стандартной цифровой клавиатуры?
Посчитаем количество комбинаций в графическом ключе(в виде пятиугольника, вершину можно использовать один раз) и в трехзначном цифровом пароле.
Графический ключ:
Выбор первого элемента можно осуществить пятью способами. Второго – четырьмя способами. Третьего – тремя способами. Четвертого – двумя способами. Пятого элемента – одним. Посчитаем всевозможные перестановки по правилу произведения и получаем:
5*4*3*2*1=120 различных комбинаций у графического ключа, разработанным Иваном.
Трехзначный цифровой пароль:
Длина пароля равна k = 3. Если считать, что нами используются буквы английского алфавита (в нем 26 букв), тогда у нас N = 26.
Максимальное количество комбинаций: M=N^k=26^3=17576. Намного больше комбинаций, чем при использовании графического ключа. То есть Иван не прав.
Ответ: Иван не прав.
00000 – ∅ пустое подмножество
Так как все нули, то подмножество будет пустым.
01110 –
Так как на 2, 3, 4 местах присутствует 1, то подмножество будет
00111 –
Так как на 3, 4 и 5 местах присутствует 1, то подмножество будет
11111 –
Так как везде присутствует 1, то подмножество будет
Можно сказать, что у множества М может быть 32 различных подмножеств.
Проверить какие из утверждений верные (теория множеств)
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Определите, какие из следующих утверждений истинны, а какие ложны
Байт, проверь правильность вот этого задания: Определите, какие из следующих утверждений истинны.
Какие из следующих утверждений справедливы
2)Ниже приведена перехваченная ресурсная запись DNS (RR resource record) в шестнадцатиричной форме.
Решение
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Какие из следующих утверждений верны
Какие верны и приведите, пожалуйста, пример таких множеств.
Модули: какие утверждения верные?
-Причины возникновения модульного программирования: возрастающие объемы программ, их.
Выяснить, какие из следующих множеств являются кольцами и какие полями
Выяснить, какие из следующих множеств являются кольцами (но не полями) и какие полями относительно.
METOD
Задача. Сравнить множество А с множествами B, C, D. Если множества пересекаются, найти их пересечения. Найти универсальное множество для данных множеств. Изобразить отношения между множествами с помощью кругов Эйлера-Венна.
Задача. Сравнить множество А с множествами B, C, D. Сравнить множества B, C, D. Найти попарно пересечение множеств В, С, D. Найти универсальное множество для данных множеств. Изобразить отношения между множествами с помощью кругов Эйлера-Венна.
курса ЧГПУ. С ∩ D – студенты-историки 1 курса ЧГПУ. U – множество всех студентов ЧГПУ.
III тип. Операции над множествами
Задача. Найти множество являющееся пересечением множеств А = и В = и мощность найденного множества. Построить диаграммы Эйлера-Венна.
По определению операции пересечения, искомое множество С будет состоять из тех и только тех элементов, которые принадлежат и множеству А и
Задача. Найти множество являющееся объединением множеств А = и В = и мощность найденного множества. Найти универсальное множество для множеств А и В. Построить диаграммы Эйлера-Венна.
По определению операции объединения, искомое множество С будет состоять из тех и только тех элементов, которые принадлежат множеству А или
Задача. Найти множество являющееся разностью множеств А = и В = и мощность найденного множества. Построить диаграммы Эйлера-Венна.
Решение. Опираясь на определения соответствующих операций над множествами, найдем пересечение, объединение и разность данных множеств.
R ∩ E = – учителя химии и биологии одновременно.
R E = – все учителя химии, биологии и учителя одновременно химии и биологии.
R \ E = – только учителя химии. E \ R = – только учителя биологии.
Ответ: R ∩ E – учителя химии и биологии одновременно, R E все учителя химии, биологии и учителя одновременно химии и биологии, R \ E
– только учителя химии, E \ R – только учителя биологии, U – все учителя.
IV тип. Доказательство свойств операций над множествами
Существует два способа доказательства равенства множеств: аналитический и графический. Воспользуемся графическим способом, а именно, изобразим с помощью кругов Эйлера-Венна операции над множествами в левой и в правой частях равенства. Если полученные множества совпадают, то равенство верно, т. е. свойство доказано.
Графическое доказательство свойств множеств
Левая часть равенства
Правая часть равенства
V тип. Задачи на множества.
Разбиение множеств. Классификация
Задача. Определить основание классификации. Проверить является ли она правильной, если нет – найти в чем ошибка:
а) меланхолик, флегматик, холерик ; б) файлы программ, служебные файлы и файлы данных;
в) естественные, искусственные, живые языки. Решение.
а) Меланхолик, флегматик, холерик – это темпераменты человека. Основание классификации – тип темперамента. Классификация неверная, так как она не полная: не хватает четвертого типа темперамента – сангвиника.
б) Файлы программ, служебные файлы и файлы данных – это типы файлов. Основание классификации – назначение файлов. Классификация правильная, так как она полная (нет файлов другого назначения и объединение этих типов файлов дает множество всех файлов) и множества файлов программ, служебных файлов и файлов данных попарно не пересекаются (например, служебный файл не может быть одновременно файлом данных и наоборот).
в) Естественные, искусственные – это классификация по происхождению языков. Живые языки – относятся к другой классификации (по применению в настоящее время). Очевидно, что классификация неверная, так как она избыточна. И к тому же, множество живых языков пересекается с множествами естественных и искусственных языков (например, русский язык является естественным и одновременно живым).
Переход от одного способа задания множества к другому
Задача. Каким способом следует задать множества в следующих ситуациях:
а) Мама говорит ребенку: «Собирай исключительно съедобные грибы»; б) Студентам перед началом летней педагогической практики
сообщают: «Подготовьтесь к работе с детьми младшего школьного возраста».
а) В данном случае множество задано характеристически, ребенку в лесу приходится задавать множество съедобных грибов перечислением: сыроежка, белый, подосиновик, подберезовик, масленок и т. д.
Принадлежность элемента множеству
Задача. Исключите лишние элементы:
а) Булгаков, Есенин, Лермонтов, Пушкин, Толстой, Шекспир.
б) Прыжки в длину, в высоту, с 10-метровой вышки, тройной прыжок. в) Клубника, арбуз, вишня, яблоко, смородина.
г) 22, 17, 180, 25006, 6, 84.
а) Представлены элементы множества А – русские писатели. Шекспир не принадлежит данному множеству.
б) Представлены элементы множества В – виды прыжков в легкой атлетике. Прыжки с 10-метровой вышки не принадлежат данному множеству.
в) Перечислены элементы множества С – ягодные культуры. Яблоко является фруктом, значит, оно не принадлежит данному множеству.
г) Общий признак у большинства чисел то, что они делятся на два, т. е. принадлежат множеству D – четные числа. 17 – не является четным числом, значит, исключается из данного множества.
Ответ: Шекспир, прыжки с 10-метровой вышки, яблоко, 17.
Подсчет количества элементов в объединении, пересечении и разности конечных множеств
Данные множества попарно не пересекаются, поэтому по правилу 2 m ( A ) + m ( B ) + m ( C ) = 6000 + 340 + 110 = 6450.
Задача. А – абитуриенты, поступающие в ЧГПУ в 2004 году. m(A) = 2000. В – студенты первокурсники ЧГПУ в 2004/2005 году, m(B) = 900. Сколько абитуриентов, не поступивших в 2004 году в ЧГПУ.
Задача. В школьной библиотеке содержатся книги с русскими текстами, книги с английскими текстами, некоторые книги, содержат как английские, так и русские тексты. Известно, что из 590 книг в 500 есть тексты на русском языке, и в 100 книгах – английские тексты. Сколько книг содержит тексты как на русском, так и на английском языке? Сколько книг содержит тексты только на русском языке? Сколько книг содержит тексты только на английском языке?
Пусть А – множество книг, содержащие тексты на русском языке, В – на английском языке. Множества А∩В пересекаются, поэтому сумма книг на русском языке и книг на английском языке (500+100 = 600) больше общего числа книг (русско-английские книги подсчитаны в сумме дважды, т. к. подсчитаны как книги с русскими текстами и книги с английскими текстами). Чтобы найти количество книг, содержащие как русские, так и английские тексты, нужно из суммы книг на русском языке и книг на английском языке (600) вычесть общее количество книг в библиотеке. Т. е. 600 – 590 = 10. Таким
образом, книг, содержащих как русские, так и английские тексты 10; книг, содержащих только русские тексты 500 – 10 = 490; книг, содержащих только английские тексты 100 – 10 = 90. Проверка: всего книг 490+10+100 = 590.
Ответ: книг, содержащих как русские, так и английские тексты 10; книг, содержащих только русские тексты 490; книг, содержащих только английские тексты 90.
Задача. В бухгалтерии мебельной фабрики было обнаружено расхождение в сведениях: за месяц общий объем изготовленных кроватей и кресел 780 единиц, но по данным из кроватного цеха кроватей выпущено 360, из кресельного цеха вышло 540 кресел. В чем причина расхождения данных, сколько на самом деле кресел и кроватей выпускают соответствующие цеха?
Один из цехов или оба цеха выпускают кресла-кровати. В отчете кресельный цех их представляет как кресла, а кроватный цех – как кровати. Пусть А – множество кроватей, В – множество кресел, А ∩ В – кресла-кровати. Тогда по правилу 4 нахождения числа элементов в объединении двух
2. Задай свойством множества, изображенные на рисунке. Какое из них является подмножеством другого? Сделай записи.
Как расположены относительно друг друга диаграммы множества и подмножества?
3. Определи по рисунку, какое из множеств является подмножеством другого.
5. Придумай примеры множества и его подмножества. Нарисуй диаграмму Эйлера-Венна.
7. Составь задачу по картинке и реши ее.
10. а) Отметь на числовом луче двузначные числа, кратные 12.
б) Выполни деление с остатком.
11. Сколько многоугольников ты видишь на чертеже?
а) На чертеже 6 многоугольников: квадрат, четырехугольник, 2 треугольника, 2 прямоугольника.
б) На чертеже 6 многоугольников: 3 треугольника, трапеция, семиугольник, шестиугольник.
Проверить какие из утверждений верные (теория множеств)
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Определите, какие из следующих утверждений истинны, а какие ложны
Байт, проверь правильность вот этого задания: Определите, какие из следующих утверждений истинны.
Какие из следующих утверждений справедливы
2)Ниже приведена перехваченная ресурсная запись DNS (RR resource record) в шестнадцатиричной форме.
Решение
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Какие из следующих утверждений верны
Какие верны и приведите, пожалуйста, пример таких множеств.
Модули: какие утверждения верные?
-Причины возникновения модульного программирования: возрастающие объемы программ, их.
Выяснить, какие из следующих множеств являются кольцами и какие полями
Выяснить, какие из следующих множеств являются кольцами (но не полями) и какие полями относительно.
Ответы по параграфу 1.3 Элементы теории множеств и комбинаторики
Задание 2. Задайте путем перечисления всех элементов:
а) множество О всех цифр, используемых для записи чисел в восьмеричной системе счисления;
б) множество К всех цепочек из 0 и 1, состоящих ровно из трех символов.
Задание 4. Обсудите в группе и запишите с помощью фигурных скобок множества:
Задание 5. Из каких элементов состоит:
а) объединение К и М;
б) пересечение К и М;
в) дополнение К до М;
г) дополнение пересечения М и А до М?
а) K ∪ M =
б) K ⋂ M =
в) дополнение К до М =
г) дополнение (M ⋂ A = ) до М =
Задание 6. В классе 35 учеников. 20 – из них занимаются в математическом кружке, 11 – в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?
Задание 7. Для составления цепочек используются бусины, помеченные буквами: M, N, O, P, S. Сколько разных цепочек можно составить из трех бусин, для которых выполняются следующие условия:
1) в середине цепочки стоит одна из бусин M, O, S;
2) третья бусина – любая гласная, если первая буква согласная, и любая согласная, если первая буква гласная;
3) на первом месте – одна из бусин O, P, S, не стоящая в цепочке в середине?
Ответ: 13 различных цепочек.
По середине у нас бусины M, O, S (1-е условие), по 3-му условию на первом месте у нас бусины O, P, S, не стоящие в цепочке в середине.
Для М на первом месте могут быть O, P, S. Для O на первом месте могут быть P, S (O не может быть на первом месте, так как в середине уже стоит такая бусина). Для S на первом месте могут быть O, P.
Чтобы выбрать третью бусину, мы придерживаемся 2-му условию. Так у нас получится 13 вариантов цепочек.
Задание 8. Сколько существует способов составить слово «ВИРУС», начиная с буквы В и двигаясь вправо или вниз до последней буквы?
Задание 9. Алла Радугина защитила свой компьютер одним из четырехсимвольных паролей, составленных из букв «А» и «Р». Сколько всего существует вариантов таких паролей? Перечислите их.
Задание 10. Каждый пользователь некой компьютерной системы получает уникальный идентификатор, представляющий собой k-символьную цепочку в четырехбуквенном алфавите. Укажите наименьшее k, позволяющее зарегистрировать в системе не менее тысячи пользователей.
Задание 11. Иван разработал приложение для планшета и защитил его оригинальным графическим ключом, использовав в качестве узлов вершины пятиугольника (каждую из вершин надо задействовать ровно один раз). Прав ли Иван, утверждая, что количество комбинаций его графического ключа ничуть не меньше, чем количество вариантов трехзначного цифрового пароля, вводимого со стандартной цифровой клавиатуры?
Посчитаем количество комбинаций в графическом ключе(в виде пятиугольника, вершину можно использовать один раз) и в трехзначном цифровом пароле.
Графический ключ:
Выбор первого элемента можно осуществить пятью способами. Второго – четырьмя способами. Третьего – тремя способами. Четвертого – двумя способами. Пятого элемента – одним. Посчитаем всевозможные перестановки по правилу произведения и получаем:
5*4*3*2*1=120 различных комбинаций у графического ключа, разработанным Иваном.
Трехзначный цифровой пароль:
Длина пароля равна k = 3. Если считать, что нами используются буквы английского алфавита (в нем 26 букв), тогда у нас N = 26.
Максимальное количество комбинаций: M=N^k=26^3=17576. Намного больше комбинаций, чем при использовании графического ключа. То есть Иван не прав.
Ответ: Иван не прав.
00000 – ∅ пустое подмножество
Так как все нули, то подмножество будет пустым.
01110 –
Так как на 2, 3, 4 местах присутствует 1, то подмножество будет
00111 –
Так как на 3, 4 и 5 местах присутствует 1, то подмножество будет
11111 –
Так как везде присутствует 1, то подмножество будет
Можно сказать, что у множества М может быть 32 различных подмножеств.
Урок 39. Пересечение и объединение множеств
Даны два множества. Первое множество состоит из букв слова «пот»,
а второе из букв слова «кот». Укажите все верные утверждения.
Из букв, входящих в пересечение указанных множеств, можно составить слово «поток».
Из букв, входящих в пересечение указанных множеств, можно составить слово «то».
Из букв, входящих в объединение указанных множеств, можно составить слово «крот».
Из букв, входящих в объединение указанных множеств, можно составить слово «поток».
Установите соответствие между множествами и их изображениями с помощью кругов Эйлера.
Укажите верное утверждение.
Нельзя начертить два треугольника, пересечением которых будет четырехугольник.
Пересечение множеств точек прямых у = 1 и х = 2 состоит из двух точек.
Пересечение множества равносторонних треугольников и прямоугольных треугольников пусто.
Объединение множества параллелограммов и множества трапеций включает в себя все возможные виды четырехугольников.
Укажите все верные утверждения.
Пересечение множества чисел, кратных 2, и множества чисел, кратных 9, является множеством чисел, кратных 18.
Объединение множеств отрицательных и положительных целых чисел является множеством всех целых чисел.
Пересечение множества целых чисел, кратных 7, и множества чисел, кратных 21, содержит числа, кратные 3.
Объединение множеств цифр, используемых в записи чисел 24523 и 42563, состоит из пяти элементов.
Контрольная «1. Продолжите предложение a) Пересечением множеств А и В называется …»,
математика
Закажите подобную или любую другую работу недорого



Вы работаете с экспертами напрямую,
не переплачивая посредникам, поэтому
наши цены в 2-3 раза ниже

Последние размещенные задания
Другое, информатика и КТ
Срок сдачи к 14 авг.
3 теоретических вопроса
Контрольная, экспертиза пожаров
Срок сдачи к 27 авг.
Автоматизированное проектирование систем ТГВ
Контрольная, Автоматизированное проектирование систем ТГВ
Срок сдачи к 21 авг.
Надо решить задачу на питоне.
Решение задач, Программирование python, Теория вероятности
Срок сдачи к 15 авг.
Задания для пересдачи
Другое, административное право
Срок сдачи к 30 авг.
нужна помощь в выполнении
Срок сдачи к 15 авг.
Сделать отчет по практике
Отчет по практике, Педагогика
Срок сдачи к 23 авг.
помощь по самостоятельной работе.
Срок сдачи к 14 авг.
Срок сдачи к 18 авг.
Необходимо решить тест более 90 баллов
Тест дистанционно, Социология
Срок сдачи к 15 авг.
помочь сделать процессуальный документ
Другое, арбитражный процесс
Срок сдачи к 14 авг.
тема: Договор: форма, содержание, виды
Курсовая, Гражданское право
Срок сдачи к 18 авг.
Решение задач по машинному обучению в информационных системах.
Решение задач, Информатика и программирование
Срок сдачи к 14 авг.
социальная поддержка семей, имеющих детей в Республике.
Курсовая, Организация работы органов и учреждений социальной защиты населения и органов Пенсионного фонда Росс
Срок сдачи к 25 авг.
Этограмма, квантификация, интерпретация поведения крысы
Срок сдачи к 25 авг.
Психология труда, инженерная психология и эргономика
Срок сдачи к 16 авг.
Рассчитать ректификацию системы ацетон-вода.
Курсовая, технология химических производств, технологическая химия
Срок сдачи к 10 сент.
Этапы подготовки и решения задач на ЭВМ
Срок сдачи к 19 авг.
обратились к нам
за последний год
работают с нашим сервисом
заданий и консультаций
заданий и консультаций
выполнено и сдано
за прошедший год

Сайт бесплатно разошлёт задание экспертам.
А эксперты предложат цены. Это удобнее, чем
искать кого-то в Интернете
Отклик экспертов с первых минут
С нами работают более 15 000 проверенных экспертов с высшим образованием. Вы можете выбрать исполнителя уже через 15 минут после публикации заказа. Срок исполнения — от 1 часа
Цены ниже в 2-3 раза
Вы работаете с экспертами напрямую, поэтому цены
ниже, чем в агентствах
Доработки и консультации
– бесплатны
Доработки и консультации в рамках задания бесплатны
и выполняются в максимально короткие сроки
Гарантия возврата денег
Если эксперт не справится — мы вернем 100% стоимости
На связи 7 дней в неделю
Вы всегда можете к нам обратиться — и в выходные,
и в праздники
Эксперт получил деньги за заказ, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы
над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем
возврат полной уплаченой суммы
Поможем вам со сложной задачкой
С вами будут работать лучшие эксперты.
Они знают и понимают, как важно доводить
работу до конца

С нами с 2017
года
Помог студентам: 10 468 Сдано работ: 10 468
Рейтинг: 76 348
Среднее 4,95 из 5

С нами с 2018
года
Помог студентам: 6 897 Сдано работ: 6 897
Рейтинг: 59 663
Среднее 4,87 из 5

С нами с 2019
года
Помог студентам: 2 191 Сдано работ: 2 191
Рейтинг: 23 080
Среднее 4,85 из 5

С нами с 2018
года
Помог студентам: 1 909 Сдано работ: 1 909
Рейтинг: 11 765
Среднее 4,86 из 5
1. Сколько стоит помощь?
Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.
Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.
3. Выполняете ли вы срочные заказы?
Да, у нас большой опыт выполнения срочных заказов.
4. Если потребуется доработка или дополнительная консультация, это бесплатно?
Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.
5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?
6. Каким способом можно произвести оплату?
Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.
7. Предоставляете ли вы гарантии на услуги?
На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.