Проведем образующую ав цилиндра так как оо1 авто прямая оо1

Боковая поверхность цилиндра

Презентацию можно использовать при изучении темы «Цилиндр»

Просмотр содержимого документа
«Боковая поверхность цилиндра»

Площадь поверхности цилиндра

2) Применить теоретические знания по данной теме к решению задач.

Две – три образующие цилиндра;

Сечение цилиндра плоскостью, проходящей через его ось;

Сечение цилиндра плоскостью, параллельной его основаниям.

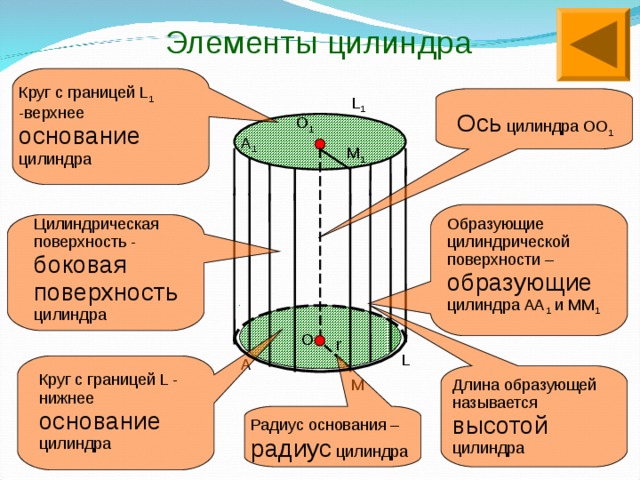
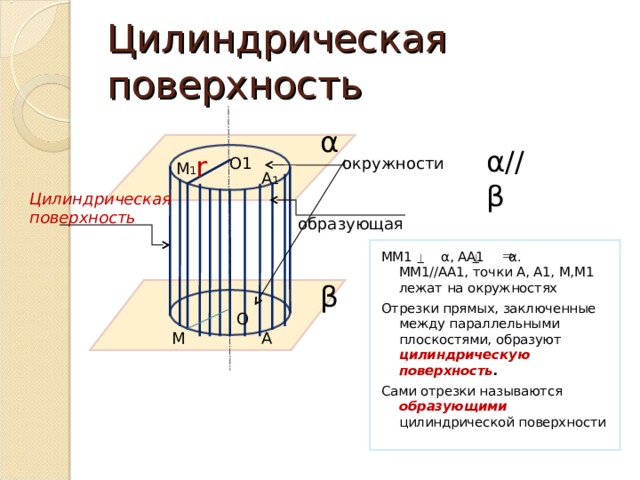
Образующие цилиндрической поверхности – образующие цилиндра АА 1 и ММ 1

Длина образующей называется высотой цилиндра

Радиус основания – радиус цилиндра

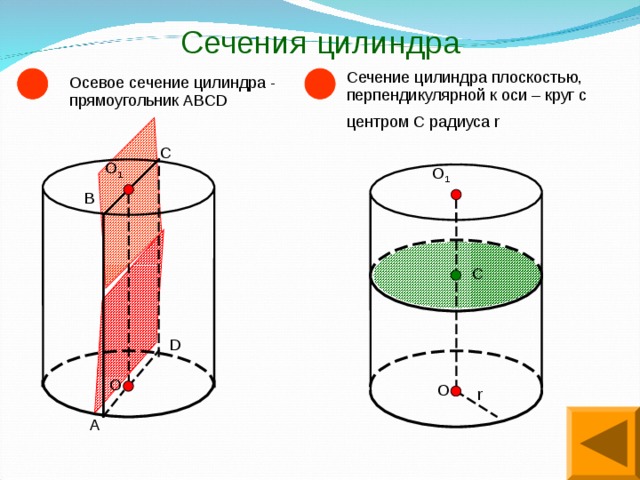
Сечение цилиндра плоскостью, перпендикулярной к оси – круг с центром С радиуса r

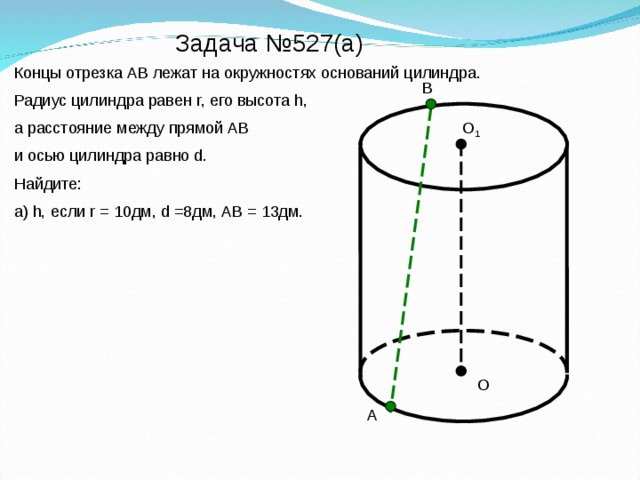
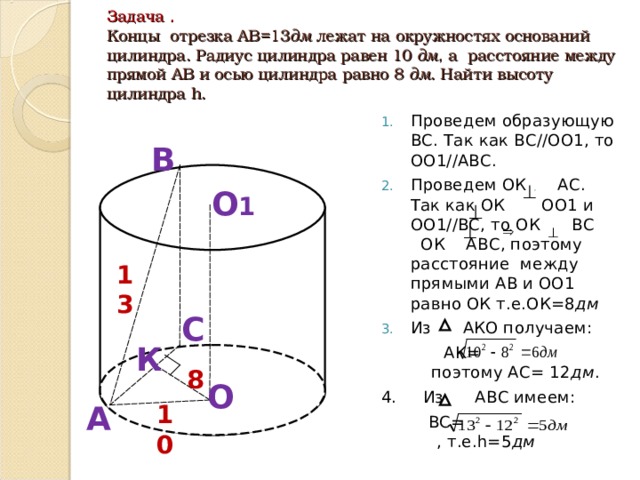
Концы отрезка АВ лежат на окружностях оснований цилиндра.

Радиус цилиндра равен r, его высота h,

а расстояние между прямой АВ

и осью цилиндра равно d.

а) h, если r = 10дм, d =8дм, АВ = 13дм.

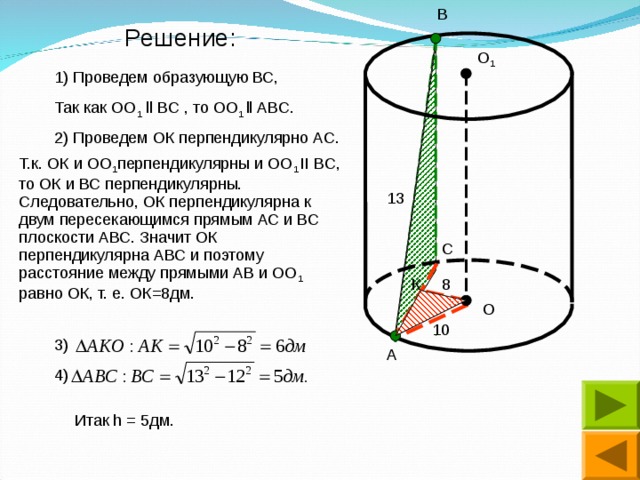
1) Проведем образующую ВС,

2) Проведем ОК перпендикулярно АС.

Т.к. ОК и ОО 1 перпендикулярны и ОО 1 II ВС, то ОК и ВС перпендикулярны. Следовательно, ОК перпендикулярна к двум пересекающимся прямым АС и ВС плоскости АВС. Значит ОК перпендикулярна АВС и поэтому расстояние между прямыми АВ и ОО 1 равно ОК, т. е. ОК=8дм.

Площадь боковой поверхности цилиндра

За площадь боковой поверхности цилиндра принимается площадь ее развертки.

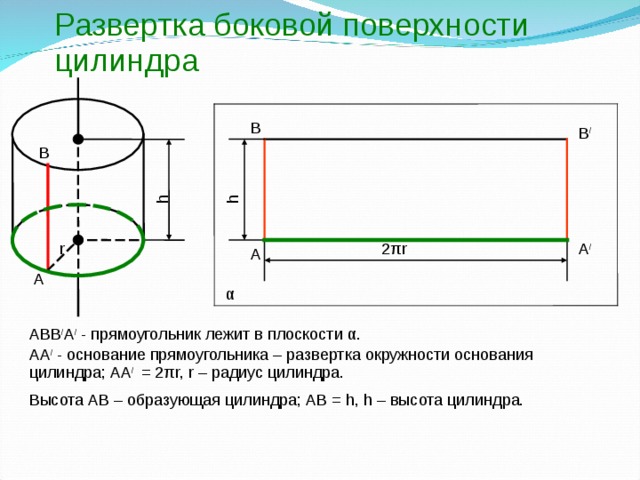
Развертка боковой поверхности цилиндра

Высота АВ – образующая цилиндра; АВ = h, h – высота цилиндра.

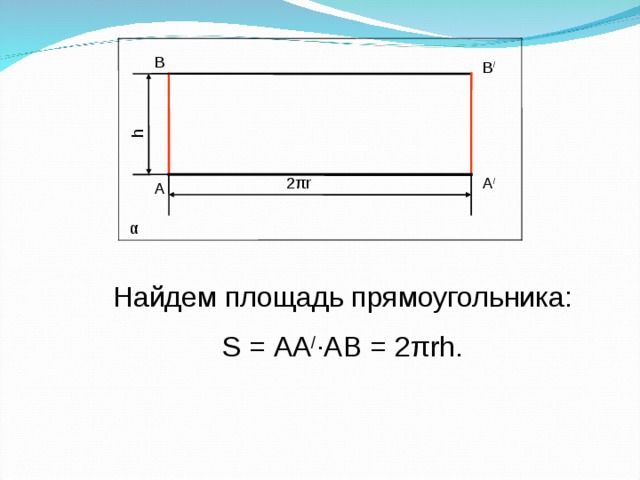
Найдем площадь прямоугольника:

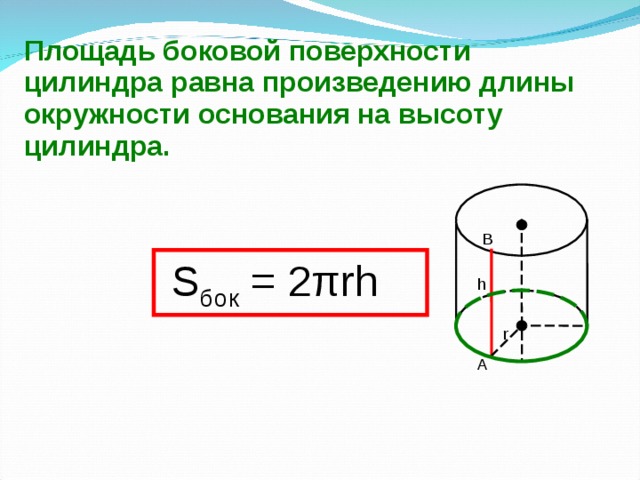
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух его оснований

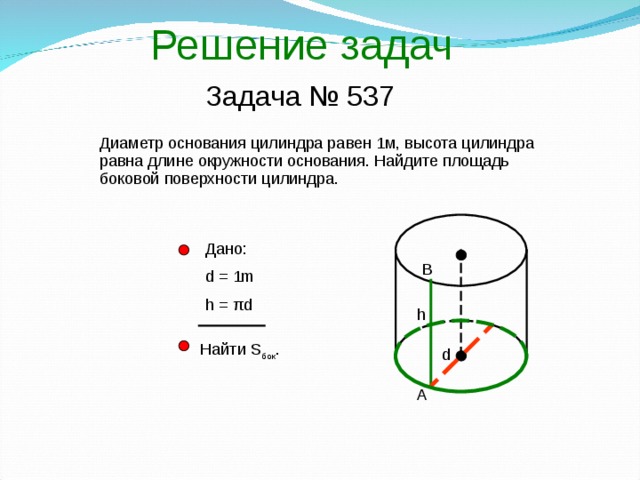
Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

новогодняя свеча цилиндр СНЕГОВИК

Источник

Презентация по геометрии на Тему «Цилиндр»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Цилиндр Площадь поверхности цилиндра

Цели урока: Ввести формулу площади поверхности цилиндра; 2)Применить теоретические знания по данной теме к решению задач.

Практическая работа Изобразите цилиндр и проведите : Две – три образующие цилиндра; Ось цилиндра; Сечение цилиндра плоскостью, проходящей через его ось; Сечение цилиндра плоскостью, параллельной его основаниям. 1. 2. 3. 4.

O r А А1 М М1 O1 Элементы цилиндра L1 L

Задача №527(а) Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, его высота h, а расстояние между прямой АВ и осью цилиндра равно d. Найдите: а) h, если r = 10дм, d =8дм, АВ = 13дм. А В О О1

Площадь боковой поверхности цилиндра За площадь боковой поверхности цилиндра принимается площадь ее развертки.

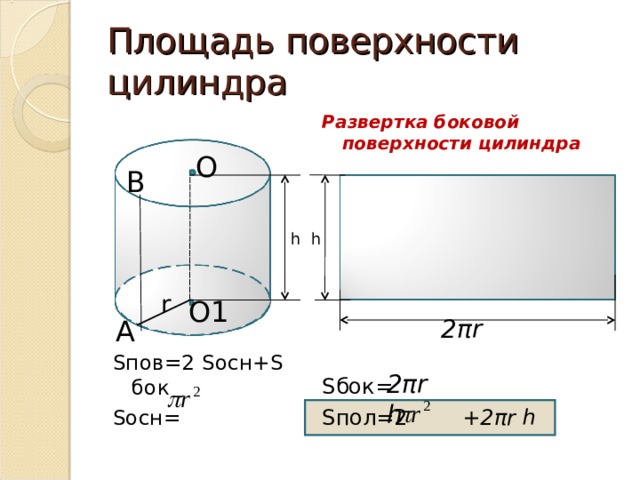
α h А В А/ В/ 2πr Найдем площадь прямоугольника: S = АА/·АВ = 2πrh.

А В r h Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра. Sбок = 2πrh

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух его оснований Sцил = 2πrh+2πr² Sцил = 2πr(r+h)

Решение задач Задача № 537 Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра. Дано: d = 1m h = πd Найти Sбок. А В d h

Решение: А В d h Sбок = 2πrh

новогодняя свеча цилиндр СНЕГОВИК

Пизанская Башня в Италии (Наклонный цилиндр)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-422361

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Псковских школьников отправили на дистанционку до 10 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Минобрнауки обновит перечень специальностей высшего образования

Время чтения: 1 минута

Учителям истории предлагают предоставить право бесплатно посещать музеи

Время чтения: 2 минуты

Утверждено стратегическое направление цифровой трансформации образования

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Понятия цилиндра

Просмотр содержимого документа
«Понятия цилиндра»

Рассмотреть типовые задачи по изучаемой теме.

Отрезки прямых, заключенные между параллельными плоскостями, образуют цилиндрическую поверхность .

Сами отрезки называются образующими цилиндрической поверхности

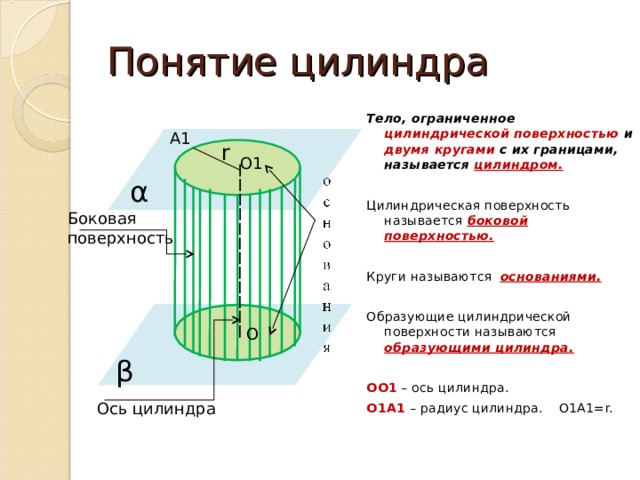
Тело, ограниченное цилиндрической поверхностью и двумя кругами с их границами, называется цилиндром.

Цилиндрическая поверхность называется боковой поверхностью.

Круги называются основаниями.

Образующие цилиндрической поверхности называются образующими цилиндра.

О1А1 – радиус цилиндра. О1А1= r.

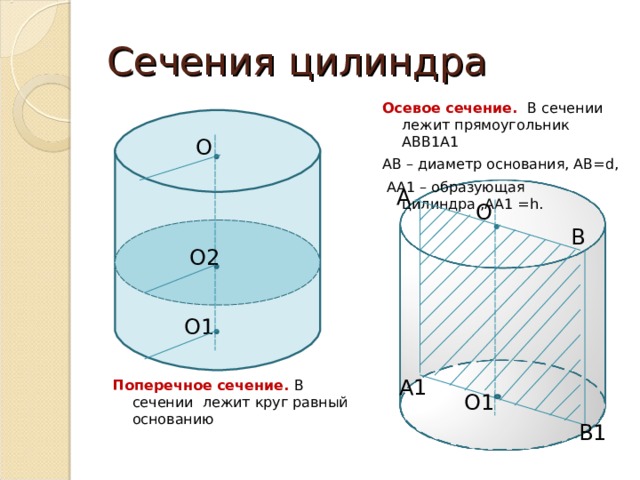
Осевое сечение. В сечении лежит прямоугольник АВВ1А1

Поперечное сечение. В сечении лежит круг равный основанию

Площадь поверхности цилиндра

Развертка боковой поверхности цилиндра

S пов= 2 S осн+ S бок

Источник

Боковая поверхность цилиндра

Презентацию можно использовать при изучении темы «Цилиндр»

Просмотр содержимого документа
«Боковая поверхность цилиндра»

Площадь поверхности цилиндра

2) Применить теоретические знания по данной теме к решению задач.

Две – три образующие цилиндра;

Сечение цилиндра плоскостью, проходящей через его ось;

Сечение цилиндра плоскостью, параллельной его основаниям.

Образующие цилиндрической поверхности – образующие цилиндра АА 1 и ММ 1

Длина образующей называется высотой цилиндра

Радиус основания – радиус цилиндра

Сечение цилиндра плоскостью, перпендикулярной к оси – круг с центром С радиуса r

Концы отрезка АВ лежат на окружностях оснований цилиндра.

Радиус цилиндра равен r, его высота h,

а расстояние между прямой АВ

и осью цилиндра равно d.

а) h, если r = 10дм, d =8дм, АВ = 13дм.

1) Проведем образующую ВС,

2) Проведем ОК перпендикулярно АС.

Т.к. ОК и ОО 1 перпендикулярны и ОО 1 II ВС, то ОК и ВС перпендикулярны. Следовательно, ОК перпендикулярна к двум пересекающимся прямым АС и ВС плоскости АВС. Значит ОК перпендикулярна АВС и поэтому расстояние между прямыми АВ и ОО 1 равно ОК, т. е. ОК=8дм.

Площадь боковой поверхности цилиндра

За площадь боковой поверхности цилиндра принимается площадь ее развертки.

Развертка боковой поверхности цилиндра

Высота АВ – образующая цилиндра; АВ = h, h – высота цилиндра.

Найдем площадь прямоугольника:

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух его оснований

Диаметр основания цилиндра равен 1м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

новогодняя свеча цилиндр СНЕГОВИК

Источник

Конспект урока на тему «Цилиндр»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Ввести понятие цилиндра, его элементов;

Закрепить понятия с помощью выполнения заданий.

Развивать пространственное воображение;

Развивать умение правильно излагать мысли;

Развивать умения анализировать, выделять главное, обобщать и делать выводы.

Воспитывать внимание, аккуратность, дисциплинированность;

Воспитывать уважительное отношение к одноклассникам и чувства собственного достоинства;

Воспитывать интерес к предмету, способствовать формированию представления о математике, как о части общечеловеческой культуры.

Познакомить учащихся с новым геометрическим телом, научить решать задачи по данной теме.

Развивать пространственное мышление учащихся, умения анализировать и систематизировать материал.

Воспитывать трудолюбие, графическую культуру учащихся.

Тип урока: урок изучения нового материала.

Продолжительность урока : 80 минут.

Оборудование урока : наглядность по теме урока, макет цилиндра, классная доска, чертежные инструменты.

Изучение нового материала.

Закрепление, решение задач.

I. Организационный момент

Здравствуйте ребята. Садитесь. Сегодня у нас на уроке присутствуют гости, покажем себя эрудированными, активными, учениками.

А теперь переходим к изучению новой темы..

С этим геометрическим телом человек знаком давно. Этому способствовали виды стволов деревьев, из которых со временем начали изготавливать балки для строительства жилищ, мостов и других сооружений. Ещё 3–4 тысячи лет назад люди научились украшать храмы и дворцы высокими колоннами, для чего из каменных глыб вытёсывали это. Древний термин названия этого происходит от греческого слова “килиндро” – вращаю, катаю. “Килиндрос” – свиток, валик. Евклид, указывая на способ образования этого, говорит, что если прямоугольник, вращающийся около одной из сторон, снова вернётся в то же самое положение, из которого он начал двигаться, то описанная фигура и будет этим геометрическим телом.

Как вы думаете, о чём идёт речь?

(Учащиеся предлагают варианты ответов)

Вот и поговорим сегодня о геометрическом теле, о цилиндре.

III. Объяснение нового материала.

Вводится понятие цилиндрической поверхности и цилиндра, даются определения боковой поверхности, оснований, образующей. Вводятся основные формулы.

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

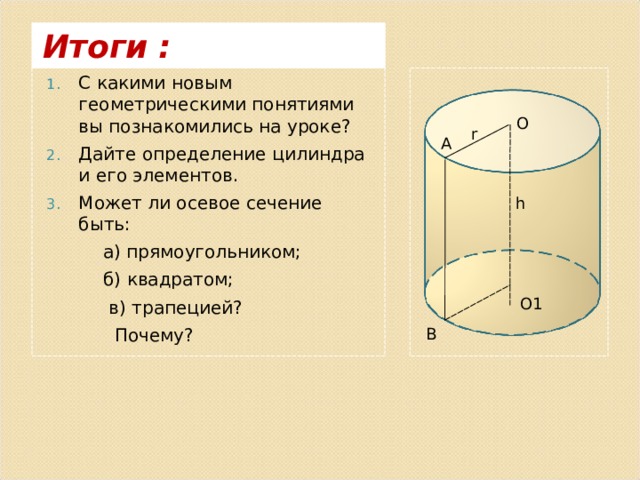
Осевое сечение цилиндра — это сечение цилиндра плоскостью, которая проходит через ось цилиндра. Это сечение является прямоугольником.

При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), также получается прямоугольник.

ABB 1 A 1 — прямоугольник.
OA = OB = R — радиусы.

При сечении цилиндра плоскостью, параллельной основанию, в сечении получаем круг, равный основаниям цилиндра.

Если представить, что боковая цилиндрическая поверхность разрезана по образующей AA 1 и развёрнута, получаем прямоугольник.

Так как развёртка — прямоугольник, то боковая поверхность определяется по формуле:

Полная поверхность цилиндра определяется по формуле:

IV. Закрепление нового материала.

Перейдем к решению задач.

Дано: Концы отрезка АВ = 13 дм лежат на окружностях оснований цилиндра. Радиус цилиндра равен 10 дм, а расстояние между прямой АВ и осью цилиндра равно 8 дм. Найти: высоту H цилиндра (см. рис. 1).

Решение: Проведем образующую ВС: Так как , то.

Проведем. Так как и, то.

Таким образом, прямая ОК перпендикулярна к двум пересекающимся прямым АС и BC плоскости АВС. Следовательно, , значит, расстояние между прямыми АВ и ОО₁ равно ОК; ОК = 8 дм.

Рассмотрим ∆АКО – прямоугольный, по теореме Пифагора: , АС=2AK=12 дм.

Рассмотрим — прямоугольный, по теореме Пифагора: .

BC – образующая цилиндра, и она равна высоте цилиндра.

Дано: Через образующую АА₁, цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра, угол между плоскостями равен φ. Найти: отношение площадей сечений цилиндра этими плоскостями.

. Значит, угол .

Теперь найдем отношение площадей, которое спрашивается: . (Угол C в треугольнике ABC – прямой, так как он опирается на диаметр нижнего основания цилиндра).

Ответ: .

Дано: Угол между образующей цилиндра и диагональю осевого сечения равен φ, Площадь основания цилиндра равна 8. Найти: площадь боковой поверхности цилиндра.

Для более удобной подстановки в формулу обозначим, что BC=2r, AB=h.

Из треугольника ABC, .

. Вместо h подставляем найденное выражение, получаем: .

В полученном выражении πr 2 =S_осн – по условию. Значит, .

Ответ: .

В данной задаче 3, можно воспользоваться только рисунком №4, не рисуя полностью весь цилиндр.

V. Подведение итога урока (фронтальный опрос).

Источник