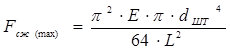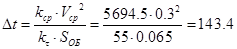Расчет амортизатора подвески автомобиля

Расчет параметров амортизатора

Расчет характеристики амортизатора

Для расчета параметров амортизатора с начало выбираем коэффициент апериодичности y=0,15…0,3, принимаем y=0,2.

,

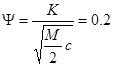
откуда коэф. сопротивления амортизатора

.

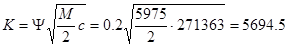
М – масса приходящаяся на подвеску, приведенная к центру колеса;

c=271363 H/м – жесткость подвески, приведенная к центру колеса;

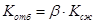
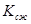
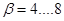
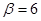
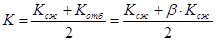
Учитывая, что коэф. сопротивления на ходе отбоя , где

— коэффициент сопротивления на ходе сжатия (, принимаем ).

,

Определяем коэффициент сопротивления на ходе сжатия амортизатора:

,

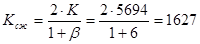
Определяем коэффициент сопротивления амортизатора на ходе отбоя:

,

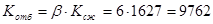
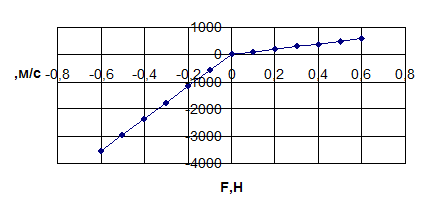
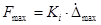
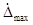
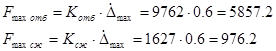
По известным коэффициентам строится характеристика амортизатора, в которой максимальная сила сопротивления: , где принимают равным 0.6 м/с.

;

Рис. 4.1. Характеристика амортизатора

Расчет параметров амортизатора

мм2,

мм,

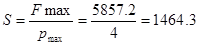
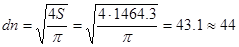
pmax=4 МПа – максимальное давление в амортизаторе;

Fmax= Fmax(отб)=5857.2 H – максимальная сила сопротивления амортизатора на ходе отбоя;

Определим диаметр штока (приняв его длину L= 300 мм)

Из расчета на устойчивость штока при максимальном осевом сжатии:

мм

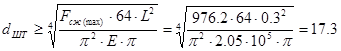
Площадь поршня на ходе отбоя

мм2,

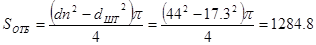
Площадь поршня на ходе сжатия

мм2,

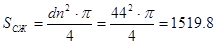
По ГОСТ выбираем амортизатор с диаметром кожуха: D=70 мм.

Гидравлический расчет амортизатора

Выбираем площадь сечения проходных отверстий такую, чтобы получить заданную характеристику.

, (1)

, (2)

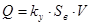
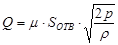
где .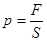

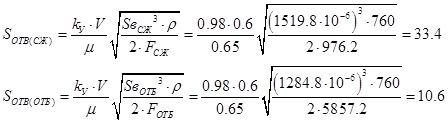
мм2

kУ=0.98 – коэф. утечек;

Sв=SвСЖ= 1519.8 мм2 – площадь вытеснителя на ходе сжатия;

Sв=SвОТБ= 1284.8 мм2 – площадь вытеснителя на ходе отбоя;

m=0.65 – коэф. расхода;

Тепловой расчет амортизатора

Мощность, рассеиваемая амортизатором в атмосферу

, (3)

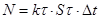
kt=55 Втм2/с – коэф. теплоотдачи;

Dt – перепад температур между поверхностью амортизатора и набегающим потоком воздуха;

Обдуваемая площадь поверхности амортизатора

м2,

. (4)

– средний коэф. сопротивления амортизатора;

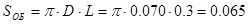
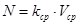
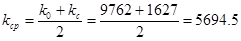
Vср=0,3 м/с – средняя скорость перемещения поршня.

Температура стенок амортизатора

0C.

Источник

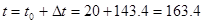
Методика Расчёта амортизатора

Расчет амортизатора проводят с целью определения его рабочих и конструктивных параметров. Основным конструктивным элементом амортизатора является диаметр его поршня d_П, который рассчитывается таким образом, чтобы наибольшее давление рабочей жидкости, соответствующее максимальному усилию, передающемуся через амортизатор, не превышало рекомендуемые пределы (2,5…5,0 МПа), а максимальная скорость перемещения поршня амортизатора (кузова автомобиля) находилась в пределах 0,3…0,5 м/с.

Отсюда диаметр дроссельного отверстий при ходе отбоя (число этих отверстий обычно равно 6):

5. Диаметр разгрузочных клапанов (поз.1 и 3 на рис.1) (их число обычно равно 6):

6. Объём компенсационной камеры, заполненный сжатым газом (поз. С на рис.1):

h_аст = 125 мм и h_ад =100 мм – полные статический (по заданию) и динамический ходы штока амортизатора соответственно; определяют с учетом выбранных статического f и динамического f_д прогибов подвески и ее передаточного отношения u.

С учетом рассчитанного объема компенсационной камеры ее длина определится как:

7. Завершая расчет амортизатора, определяют общую длину амортизатора l_а :

По результатам самостоятельного изучения материала и проведенных расчетов оформить отчет по работе и подготовить его к защите.

Практическое занятие №11по теме «Несущая система автомобиля»

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Герб Адамс — Разработка шасси. Глава 5. Пружины и амортизаторы (Часть 1)

ГЛАВА 5. ПРУЖИНЫ И АМОРТИЗАТОРЫ

Пружины и амортизаторы являются неотъемлемой частью подвески любого типа. Но общая система подвески должна рассматриваться как согласованный пакет, поэтому простая замена пружин и/или амортизаторов не всегда приведёт к желаемому результату. То, что работает на одном автомобиле, может не работать на другом автомобиле из-за различий в их конструкции. При выборе пружин и амортизаторов для вашего автомобиля следует учитывать следующие аспекты.

5.1 НАГРУЗКА ПРУЖИНЫ И ЕЁ ЖЁСТКОСТЬ
Пружинную нагрузку и жёсткость пружины часто путают. Для лучшего понимания того, как работает ваша подвеска, важно осознать эту разницу.
Нагрузка пружины — это величина веса, выраженная в кгс, которая потребуется для сжатия пружины на заданную высоту.
Жёсткость пружины — это величина веса, выраженная в кгс/см, которая потребуется, чтобы сжать пружину на один сантиметр (*т.е. это удельная пружинная нагрузка).
Пример этой взаимосвязи пружин приведен в табл. 5-1.

Табл. 5-1. Типичная задняя пружина
╔══════════════╦══════════════════╦═══════════════╗
║Сжатие пружины, см ║ Жёсткость пружины, кгс/см║ Нагрузка пружины, кгс║
║______________ 2.54║___________________ 26.8║_________________68║
║______________ 5.08║___________________ 26.8║________________136║
║______________ 7.62║___________________ 26.8║________________204║
║_____________ 10.16║___________________ 26.8║________________272║
║_____________ 12.70║___________________ 26.8║________________340║
║_____________ 15.24║___________________ 26.8║________________408║
║_____________ 17.78║___________________ 26.8║________________476║
║_____________ 20.32║___________________ 26.8║________________544║
╚══════════════╩══════════════════╩═══════════════╝

Обратите внимание, что при сжатии пружины её жёсткость не изменяется, а нагрузка — меняется. В табл. 5-1 на каждые 68 кгс нагрузки пружина сжимается на 2.54 см (1 дюйм). Жёсткость пружины определяет на сколько пружина будет сжиматься по мере увеличения нагрузки. Нагрузка пружины определяет сколько веса пружина может поддерживать на заданной высоте. Например, когда пружина сжимается на 17.78 см, она держит 476 кгс нагрузки. Если один из углов вашего автомобиля просел, то вам не нужна пружина бОльшей жёсткости, вам нужна пружина бОльшей нагрузки.

5.1.2 Жёсткость на колесе против жёсткости пружины
Эта взаимосвязь часто сбивает с толку, когда энтузиасты пытаются непосредственно измерить результаты. Жёсткость на колесе — это фактическая жёсткость пружины на колесе, а не жёсткость самой пружины. Это не простая взаимосвязь, поэтому добавление 17.8 кгс/см к жёсткости пружины не добавит 17.8 кгс/см к жёсткости на колесе, только если пружина не установлена непосредственно на оси. Всегда, когда есть связи, такие как задействованные рычаги подвески, вам необходимо учитывать коэффициенты передачи. Поскольку большинство современных автомобилей используют верхние и нижние рычаги на передней подвеске, мы воспользуемся этим примером, чтобы продемонстрировать как работают коэффициенты передачи. На рис. 5-1 показана схема типичной передней подвески с верхними и нижними рычагами подвески и пружиной, действующей на нижний рычаг. Формула для определения жёсткости на колесе:

Жёсткость на колесе = Жёсткость пружины × (A/B)² × (C/D)²,

где
A — расстояние от внутреннего шарнира нижнего рычага до центральной точки действия пружины;
B — расстояние от внутреннего шарнира нижнего рычага до его шаровой опоры;
C — расстояние от шаровой опоры нижнего рычага до мгновенного центра скоростей;
D — расстояние от середины пятна контакта шины до мгновенного центра скоростей.

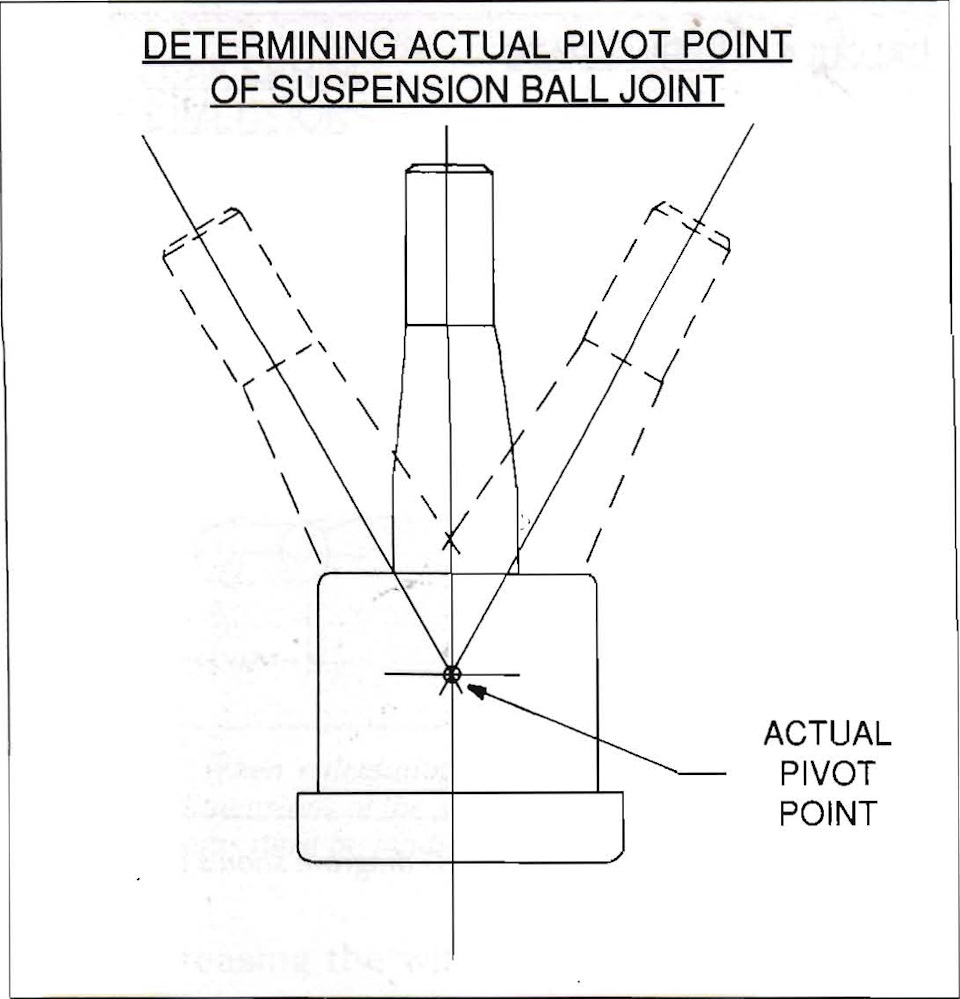
Определение мгновенного центра скоростей. Чтобы точно найти мгновенный центр скоростей передней подвески, вам нужно сделать масштабный чертёж, основанный на измерениях, сделанных на автомобиле, установленном на ездовой высоте. Это звучит трудоёмко, но вы можете сделать это с рулеткой примерно за час. Чтобы получить достоверные результаты, нет необходимости измерять точнее 0.16 см. Однако, следует озаботиться определением фактической точки поворота шаровых опор. Её трудно определить, так как она находится внутри шарнира. Если у вас есть шаровая опора от автомобиля, то вы можете сдвинуть её из одного крайнего положения в другое и на глаз определить фактический центр вращения. Он обычно близок к фланцу или к концу корпуса, поэтому вы можете использовать его в качестве контрольной точки при проведении измерений на вашем автомобиле (рис. 5-2).

Когда вы сделаете схему своей передней подвески, у вас будут размеры A, B, C и D, необходимые для подстановки в уравнение жёсткости на колесе. В целях дальнейшего пояснения предположим, что вы имеете следующие размеры:

A = 22.86 см
B = 35.46 см
C = 228.6 см
D = 238.76 см

Если эти размеры подставить в формулу, то с пружиной жёсткостью 89.29 кгс/см получатся следующие результаты:

Жёсткость на колесе = 89.29 × (22.86/35.46)² × (228.6/238.76)² ≈ 33.83 кгс/см

Обратите внимание, что при такой конфигурации жёсткость на колесе составляет 37.9% от жёсткости пружины. Это означает, что добавление 10 кгс/см к жёсткости пружины добавит лишь 3.79 кгс/см к жёсткости на колесе.

Используя этот же пример, давайте посмотрим, что произойдёт когда крепление пружины на нижнем рычаге подвески сдвинется на 2.54 см наружу:

A = 25.4 см
B = 35.46 см
C = 228.6 см
D = 238.76 см

Жёсткость на колесе = 89.29 × (25.4/35.46)² × (228.6/238.76)² ≈ 41.76 кгс/см

Эта жёсткость на колесе составляет около 46.77% от жёсткости пружины, поэтому перемещение точки крепления пружины на 2.54 см наружу увеличивает жёсткость на колесе больше, чем добавление 10 кгс/см к жёсткости пружины.

Из-за влияния коэффициентов передачи, как правило, невозможно сравнивать жёсткости пружин одного автомобиля с жёсткостями пружин другого автомобиля, только если не известны размеры всех связей. Из приведенных выше примеров также очевидно, что простое использование колёс с бОльшим или меньшим вылетом будет иметь некоторое влияние на фактическую жёсткость на колесе (*уменьшение ET приводит к уменьшению жёсткости на колесе).

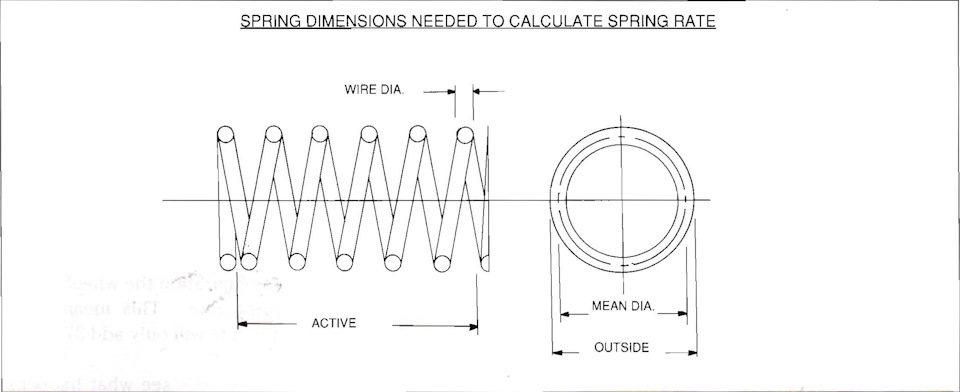
5.1.3 Расчёт жёсткости винтовых пружин
Если у вас есть доступ к измерителю жёсткости пружин, то вы можете измерить жёсткость всех ваших пружин. Если у вас нет измерителя жёсткости, то вы также можете определить жёсткость ваших пружин, сняв их размеры и воспользовавшись следующей формулой:

Жёсткость винтовой пружины = G(d²)²/(8ND³),

где
G — модуль сдвига материала пружины, для стали 79300 МПа;
d — диаметр прутка пружины, мм;
N — число рабочих витков;
D — срединный диаметр витков, мм.

Коэффициент G в уравнении для цилиндрических пружин, изготовленных из стали, всегда один и тот же. Для титановых пружин потребуется другой коэффициент (*41400 МПа, титан мягче).

Диаметр прутка пружины d можно измерить с помощью штангенциркуля. Он будет одинаков по всей длине пружины, только если это не пружина переменной жёсткости, и в этом случае вы не можете подставить этот размер в формулу. Для нашего примера мы предположим, что диаметр прутка составляет 15.75 мм.

Определение количества активных витков требует определённого решения с вашей стороны. Механическая обработка играет роль. Если концы пружины сплющены или механически обработаны, то эти витки неактивны, так как они покоятся на своих монтажных площадках. При подсчёте действующих витков учитывайте только те, которые могут перемещаться по мере сжатия пружины. Предположим, например, что пружина имеет 10 активных витков.

Определение срединного диаметра пружины можно выполнить с помощью рулетки, начиная с конца пружины, как показано на рис. 5-3. В нашем примере мы предположим, что срединный диаметр витка составляет 127 мм. Подставляя в формулу эти размеры, получим:

Жёсткость винтовой пружины = 79300∙(15.75²)²/(8∙10∙127³) ≈ 29.78 кгс/см.

Из этого расчёта следует отметить несколько вещей.

1. Если мы срежем один виток пружины, то у неё будет меньше активных витков, длина пружины изменится, а жёсткость будет увеличена:
Жёсткость винтовой пружины = 79300∙(15.75²)²/(8∙9∙127³) ≈ 33.09 кгс/см.
Это примерно на 11% больше, что пропорционально количеству срезанных витков.

2. Увеличение диаметра прутка приведёт к резкому увеличению жёсткости пружины. Если мы увеличим диаметр прутка только на 0.8 мм, то жёсткость пружины будет равна
Жёсткость винтовой пружины = 79300∙(16.55²)²/(8∙9∙127³) ≈ 40.34 кгс/см.

3. Ничто в расчёте жёсткости пружины не указывает на то, что винтовая пружина когда-либо меняет свою жёсткость. Жёсткость определяется материалом (сталью в нашем случае) и размерами пружины. Винтовые пружины не изнашиваются и не теряют жёсткость.

4. Ничто в расчёте жёсткости пружины не описывает пружинную нагрузку. Пружинная нагрузка определяет, сколько веса пружина может поддерживать на заданной высоте. Жёсткость пружины указывает только то, насколько изменится высота при изменении нагрузки. Пружина может потерять свою нагрузку с течением времени (*релаксировать) или если сталь не подвергалась термообработке должным образом. Тем не менее, когда пружина проседает, её жёсткость остаётся такой же, как когда она была новой.

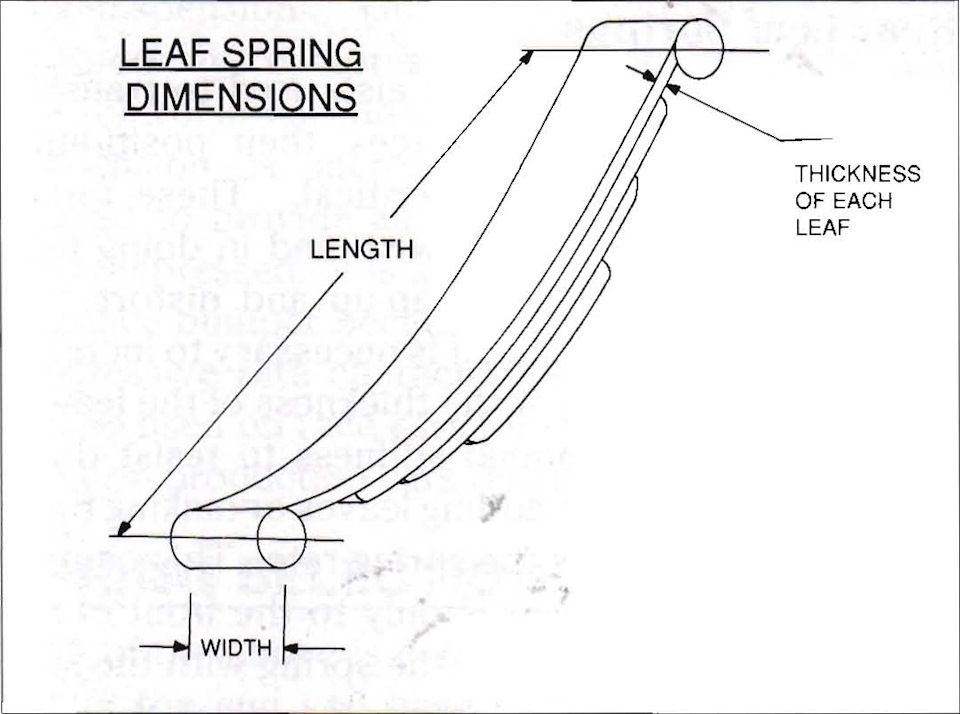
5.1.4 Расчёт жёсткости листовых рессор
Жёсткость листовой рессоры (*пластинчатой пружины) определяется её физическими размерами, как показано на рис. 5-4. Жёсткость листовой рессоры может быть аппроксимирована следующей формулой:

Жёсткость листовой рессоры = (WN/12) × (1000∙t/L)³,

где
W — ширина листов, мм;
N — число листов;
t — толщина одного листа, мм;
L — длина пружины, мм.

В качестве примера предположим следующие размеры:

W = 7.62 см;
N = 5;
t = 0.635 см;
L = 152.4 см.

Подстановка этих значений в формулу приводит к:

Жёсткость листовой рессоры = (W∙5/12) × (1000∙0.635/152.4)³ ≈ кгс/см.

5.2 ГДЕ УСТАНАВЛИВАТЬ ПРУЖИНЫ
Места установки пружин так же важны, как и их жёсткости. Эти факторы надо учитывать как на существующем автомобиле, так и на вновь проектируемом.

5.2.1 Передние пружины
Чтобы свести к минимуму влияние коэффициента передачи, обычно передние пружины лучше всего монтировать как можно ближе к шаровой опоре. Существуют очевидные соображения о допустимости монтажа, который должен быть разрешим, но в целом, чем ближе, тем лучше. На автомобилях Winston Cup, которые всё ещё используют пятидюймовые пружины, невозможно установить пружины очень близко к шаровой опоре. Это приводит к большому передаточному коэффициенту и потребности в пружинах очень высокой жёсткости. Также хорошей политикой является крепление пружин в как можно более вертикальном положении, чтобы иметь силу пружины в её полном объёме.

5.2.2 Задние винтовые пружины
Часто имеется возможность устанавливать задние винтовые пружины непосредственно на корпусе оси. Такая конфигурация создаёт жёсткость на колесе, равную жёсткости пружины. Задние пружины также могут быть установлены на задних рычагах подвески, но, поскольку это приводит к рассмотрению коэффициента передачи, жёсткость на колесе уже не будет такой же, как жёсткость пружины.

При установке задних пружин также необходимо учитывать угол наклона пружин относительно вертикали, так как этот угол может влиять на фактическую силу пружины. Установка пружин под углом к вертикали может уменьшить эффективное усилие, которое пружина обеспечивает в вертикальном направлении. Небольшое отклонение имеет небольшой влияние, но угол более 30° приведёт к значительному уменьшению вертикальной силы на оси и, соответственно, уменьшению эффективности пружины.

5.2.3 Задние листовые рессоры
Поскольку задние листовые рессоры используются также для передачи ускоряющих и тормозных усилий, их местоположение и форма являются более критичными. Эти силы заставляют корпус оси закручиваться, и при этом листовые рессоры имеют тенденцию к скручиванию и искажению. Чтобы противодействовать такому состоянию, необходимо увеличить количество листов или их толщину, чтобы дать рессоре достаточную угловую жёсткость для противостояния этим силам. К сожалению, добавление листов или их толщины увеличивает жёсткость рессоры в целом. Это противоречие решается путём добавления листов только к передней части рессоры, что даёт рессоре жёсткость в её передней половине, необходимой для противодействия реакции от крутящего момента на оси, при этом не увеличивая вертикальную жёсткость пружины в той мере, как если бы был добавлен полный лист. Именно по этой причине большинство листовых рессор, используемых на гоночных автомобилях, имеют дополнительные листы только на своей передней части.

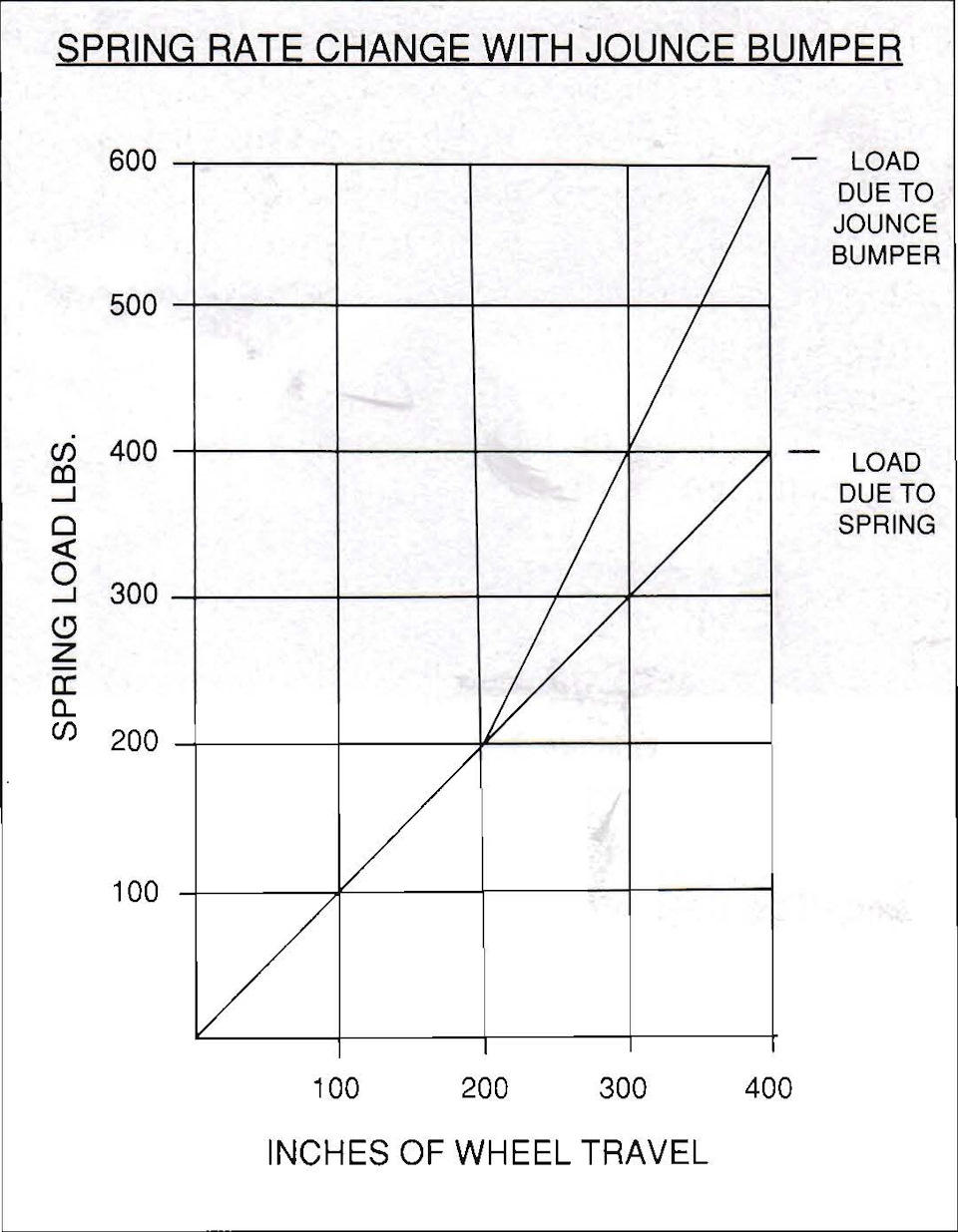
5.3 ОГРАНИЧИТЕЛИ ХОДА ПОДВЕСКИ
Ограничители хода подвески (буферы-отбойники) — это резиновые блоки, которые удерживают нижние рычаги подвески от удара о раму или кузов при сильных толчках. Многие энтузиасты выбрасывают их, что является ошибкой, поскольку они не осознают, что эти буферы в действительности являются пружинами переменной жёсткости. Используя буферы-отбойники, становится возможным использование более мягких пружин. В свободном ходе перед тем, как отбойники касаются рамы или кузова, только автомобильные пружины являются активными элементами подвески. При сильных ударах буферы-отбойники сжимаются между рамой и рычагами подвески, при этом эффективная жёсткость пружины увеличивается. Буферы-отбойники имеют форму, обеспечивающую всё возрастающую жёсткость по мере их сжатия. Ошибочно обрезать форму буфера-отбойника, поскольку это разрушает его прогрессивную характеристику жёсткости. Буферы-отбойники могут использоваться на гоночных автомобилях по тем же причинам, по которым они используются на серийных автомобилях (рис. 5-5).

5.4 ВЫБОР ПРУЖИН
Всё вышесказанное является хорошей справочной информацией, но в конце концов вы должны принять решение о том, какие пружины использовать на своём автомобиле. Понимание всех задействованных факторов поможет принять это решение, а также поможет рационализировать пружины, которые вы уже используете. Ниже приведены некоторые из факторов, которые следует учитывать при выборе пружин для вашего автомобиля.

5.4.1 Аэродинамические эффекты
Некоторые гоночные автомобили, такие как Indycar, могут иметь аэродинамическую прижимную силу, превышающую вес автомобиля. Если у вас 1360 кг автомобиль с 1360 кгс прижимной силы, то вам потребуются жёсткость и нагрузка пружины вдвое большие, чем при нулевой аэродинамической прижимной силе. Заводской автомобильный кузов на треке длиной 1/4 мили не имеет большой аэродинамической прижимной силы, но некоторые модифицированные автомобили имеют её значительную величину.

5.4.2 Жёсткость пружин слева и справа
Автомобили, используемые на круговых трассах, имеют большой процент веса, переносимого во время поворота на правый борт. Поскольку эффективный вес с правой стороны автомобиля увеличивается, там потребуется пружина бОльшей жёсткости и нагрузки. Установка более мягких пружин с левой стороны является популярным выбором, поскольку это не нарушает общий баланс автомобиля. Скоростные дорожные и уличные автомобили обычно используют пружины одних и тех же жёсткостей и нагрузок с левой и правой стороны, потому что они испытывают как левый, так и правый повороты.

5.4.3 Эффекты от слишком жёстких пружин
Так как большинство гоночных автомобилей могут регулировать пружинную нагрузку для установки правильной ездовой высоты, выбор наилучшей жёсткости пружины обычно вызывает наибольшую озабоченность у гонщиков. Мы обсудили причины, по которым может потребоваться бОльшая жёсткость пружин, но как узнать не слишком ли жёсткие у вас пружины? Как правило, лучше всего использовать как можно более мягкую пружину. Сцепление между автомобильными шинами и дорогой является единственным источником развития поворачивающей силы. Если шины теряют контакт с дорогой, то они создают нулевую силу для поворота. Мягкие пружины позволяют шинам лучше следить за дорожными ухабами и неровностями, поэтому шины остаются в контакте с дорогой в течение большего процента времени. Более высокая жёсткость пружины также может ограничить ход подвески как на сжатие, так и на отбой. Если ваш автомобиль не получает полного хода подвески, то, возможно, это не позволит шинам следовать по дороге в максимально возможной степени.

Пружины переменной жёсткости. Изучение оптимальных жёсткостей пружин для автомобиля в конечном итоге приводит к выводу, что наилучшая жёсткость пружины является переменной величиной. Мы хотели бы иметь мягкую пружину, чтобы поглощать дорожные неровности, а затем иметь высокую жёсткость пружины, чтобы поглощать большие удары. Имеются пружины, которые изготовлены с переменной жёсткостью. Вы можете определить эти пружины, заметив, что расстояние между витками отличается от одного конца к другому. Конструкторское решение для этих пружин верное, но на практике они не работают слишком хорошо. Поскольку автомобильные пружины работают только в ограниченной части от общего хода подвески, величина изменения в их жёсткости обычно довольно мала. Буферы-отбойники обеспечивают такую же функцию переменной жёсткости, но с большей согласованностью.

5.4.4 Жёсткость пружин для овальных трасс
Когда автомобиль движется по овальной трассе с наклоном, жёсткость пружин должна быть увеличена, дабы компенсировать увеличение эффективного веса автомобиля. В табл. 5-2 приведены приблизительные значения процента увеличения жёсткости пружин для разных углов наклона трасс. Эти расчёты выполнены для автомобиля, испытывающего перегрузку 1 на поворотах для всех углов наклона трассы. Поскольку автомобиль может не поддерживать такую перегрузку в поворотах из-за аэродинамики или мощности, эти цифры могут быть завышенными при некоторых обстоятельствах. Эти значения близки, но автомобиль и водитель должны быть последними элементами при выборе жёсткости пружин на любом заданном треке.

Табл. 5-2.
╔═══════════════╦════════════════════════╗
║Угол наклона трассы, °║Приращение жёсткости пружины, % ║
║__________________0║_____________________________ 0║
║__________________5║____________________________ 10║
║_________________10║____________________________ 23║
║_________________15║____________________________ 41║
║_________________20║____________________________ 67║
║_________________25║___________________________ 106║
╚═══════════════╩════════════════════════╝

5.4.5 Жёсткость пружин для уличного применения
Цель пружин подвески — удерживать автомобиль в спокойном состоянии, при этом позволяя колёсам отслеживать неровности дороги. В общем, самые мягкие пружины будут делать эту работу лучше всего. Более мягкие пружины позволяют каждому отдельному колесу перемещаться относительно шасси при минимальном воздействии на кабину водителя. Это приводит к мягкой езде, шумоизоляции и хорошей управляемости.

Более жёсткие пружины делают езду автомобиля жёсткой. У них нет возможности значительно улучшить управляемость. До тех пор, пока пружины на автомобиле достаточно жёсткие для того, чтобы автомобиль не цеплял днищем, они адекватны. Если автомобиль занижен, то небольшое увеличение жёсткости пружин может быть использовано для компенсации уменьшенного хода подвески.

Некоторые автомобильные энтузиасты ошибочно полагают, что если пружины жёсткостью 20 кгс/см хороши, то пружины жёсткостью 40 кгс/см должны быть ещё лучше. Они ошибаются. Оптимальное сцепление с дорогой требует, чтобы шины находились в контакте с дорожным покрытием; мягкая пружина позволяет колёсам отслеживать неровности дороги, так что шины могут создавать максимальное сцепление.

Наша рекомендация для передних пружин на уличных автомобилях — использовать стандартные заводские пружины. Чтобы немного опустить автомобиль для уличного использования, вы можете отрезать одну половину витка с верхней части пружины, используя ацетиленовую горелку.

Большинство передних пружин имеют жёсткость от 50 до 60 кгс/см. Обрезка витка, как мы рекомендовали, увеличит жёсткость примерно на 10%. Но истинная цель обрезки передних пружин — занизить автомобиль для улучшения аэродинамики и управляемости, а не для увеличения жёсткости пружины.

Некоторые автомобили, таких как Corvette с подвеской F-41, Pontiac WS-6 Trans Am и более поздняя модель Chevrolet Camaro Z-28, оснащены очень жёсткими пружинами. Мы обнаружили, что езда может быть значительно улучшена за счёт установки более мягких пружин, не влияя на возможности управляемости этих автомобилей. Многие энтузиасты покупают для этих автомобилей стандартные мягкие пружины у своего дилера и отрезают 1/2 витка для правильной ездовой высоты.

Источник