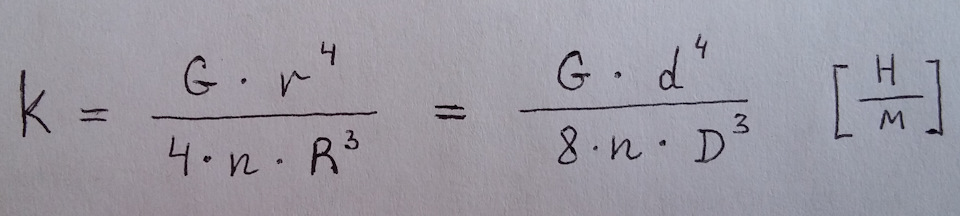Расчет пружин подвески автомобиля
Расчет и замена пружин подвески.
(дублирую в журнале по машине)
Продолждаем борьбу с врожденными болячками платформы K2, с подвеской моего Hyundai Solaris.
После вставления ему углов основная проблема с подруливаниями на неровностях была радикально уничтожена в зародыше, но осталась другая проблема. В попытках завода решить это проблему методом «давайте в случае головной боли отрубим голову» получили жесткую телегу, которая скачет как теннисный мячик по кочкам и громко бахает на ходе отбоя после проезда лежачих полицейских.
Да, я в курсе, что основное массонаселение в таких случаях делает «что попало» ну или советуется с форумными троллями. Но это не мой метод. Для изменения чего-то в машине для начала надо изучить как все устроено, и явно не на форумах для домохозяек и не в соц.сетях. В качестве литературы могу порекомендовать книгу Вахламов В.К. «Теория и конструкция автомобиля и двигателя»(есть на рутрекере). И книгу Емельянова А.Е «Расчет цилиндрических пружин подвески автомобиля с нелинейной характеристикой упругости»
Итого пару полезных формул оттуда:
Формула расчета коэффициента жесткости пружины: k = G * (d)^4 / 8 * n * (D)^3
Формула расчета колебаний неподрессоренных масс: Fn = (sqrt(k/m)) / 2pi (в минуту)
Можно конечно еще больше углубится в дебри расчетов, но на первом этапе именно этих двух понятий будет более чем дотаточно.
Но не буду повторятся, все это смотрим в небольшой лекции на тему с проверкой на практике в конце:
Расчёт жёсткости пружин подвески
Здравствуйте! Поговорим или попишем о пружинах подвески.
Пост для того, чтобы не забыть и для того, чтобы ознакомить Вас, читатели 🙂
Предыдущая моя запись была про подвеску. На этот раз разберём самый интересный, на мой взгляд, компонент пружину подвески. Пока речь пойдёт про передние пружины, позже я добавлю и задние, когда доберусь до них, сниму мерки и метки. Давненько не даёт мне покоя эта тема, поэтому сведу всё в одну запись.
Предыстория простая — иметь возможность подобрать то, что нужно под конкретный запрос.
Итак, для расчёта жёсткости пружины необходима следующая формула:
где
G — модуль сдвига;
n — количество витков;
r — радиус прутка;
d — диаметр прутка;
R — радиус навива;
D — диаметр навива.
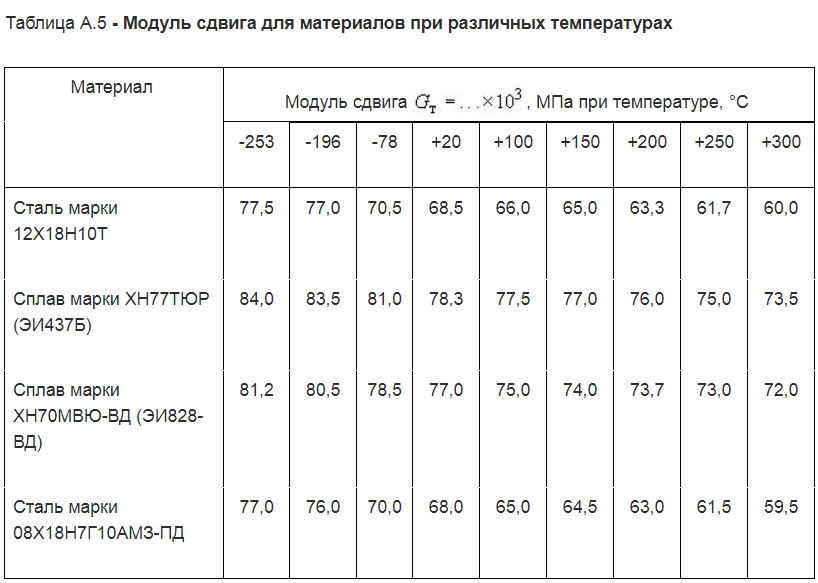
Для классической пружинной стали модуль сдвига, как правило, принимает значение 78,5 ГПа (или же 7850 кгс/ мм2). Однако, всё зависит от марки стали, которую закладывают производители. Тем не менее, модуль сдвига стали будет, так или иначе, находиться в диапазоне от 77 до 85 ГПа.
В РФ есть ГОСТ на такую вещь. Параметры приведу в табличной форме:
Какие выводы можно сделать?
1. Коэффициент жесткости не зависит от длины пружины, но зависит от количества витков, поэтому когда мы срезаем один или два витка, происходит увеличение коэффициента жесткости.
2. Увеличение толщины прутка на 10 процентов при тех же остальных параметрах дает увеличение коэффициента жесткости почти на 50 процентов. Это связано с тем, что коэффициент жесткости прямопропорционален диаметру прутка в четвертой степени.
3. Коэффициент жесткости зависит от материала, из которого сделана пружина.
Если верить каталогу, то мы можем любую понравившуюся нам пружину купить, благо артикул есть. Можно попытаться посмотреть аналоги в известных интернет магазинах.
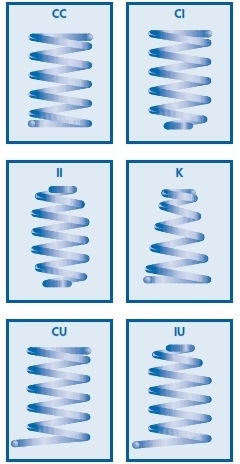
В каталоге есть легенда по параметрам пружин:
А так же легенда по типам пружин:
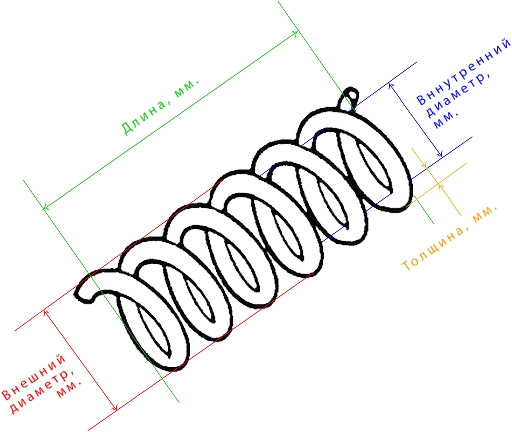
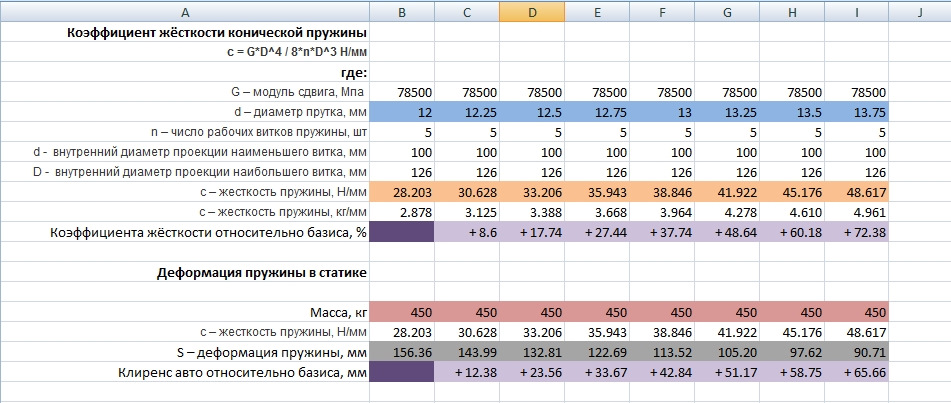
Для наглядного понимания, что нам всё это даёт я сделал расчёт в Exel коэффициентов жёсткости на основании своих измерений и линейных деформаций при условии нагрузки на одну пружину 450 кг. Эту цифру я получил при известной массе автомобиля 1300 кг, а так же примерной развесовки 70х30 перед/зад.
Расчёты выполнены для конической пружины, хотя в нашем варианте она не совсем коническая. Параметр внутренний диаметр наименьшего витка указан приблизительно. Вообще пружина цилиндрическая, кроме верхнего витка.
Теперь поговорим о клиренсе в стационарном режиме. Клиренс определяется как раз изменением длины пружины под действием силы тяжести.
Если мы хотим сохранить клиренс, но ужесточить подвеску, нам необходимо изменить параметр х в сторону уменьшения за счет увеличения коэфициента жесткости, при этом на столько же, насколько изменили значение х, необходимо выбрать пружину короче. Если мы увеличим только жесткость, но при этом длина пружина останется прежней, авто станет жестче, но при этом приподнимется.
Если мы хотим приподнять машину, но сохранить жесткость, то необходимо использовать более длинные пружины, но с тем же коэффициентом жесткости. На чем хотелось бы сакцентировать внимание: если происходит изменение клиренса одной из осей, а клиренс второй оси остается прежний, то автоматически происходит изменение распределения веса по осям. Если мы приподняли заднюю часть, то баланс веса смещается вперед, соответственно, сила, действующая на задние пружины становится меньше, а значит и параметр х тоже уменьшается. Этот прием часто применяется для снижения вероятности пробуксовки передней оси на переднеприводных автомобилях. Наиболее популярный метод сохранения жесткости с увеличением клиренса — это установка проставок под те же пружины или на опорную чашку. При таком подходе сама пружина сжимается под весом авто почти так же, как и до доработки, с небольшой поправкой на перераспределение веса по осям, но за счет проставок дорожный просвет увеличивается на толщину проставки.
Параметр х очень важен для стойки, так как у штока аммортизатора имеется некоторый участок примерно в треть длины, который в стационарном состоянии должен находиться внутри аммортизатора. Это необходимо для того, чтобы аммортизатор работал не только на отбой, но и на разгрузку. Если Вы поставите пружины настолько жесткие, что после опускания автомобиля с домкрата пружина не сожмется на необходимый ход штока, то в процессе эксплуатации аммортизаторы очень быстро выйдут из строя. Кроме того, неправильно подобранное значение х повлияет и на управляемость автомобиля — неправильно настроенная ось будет подпрыгивать на каждой кочке и в поворотах.
Ну, и в заключение поговорим о понятии «преднатяг». Если пружина ставится соосно с аммортизатором, то преднатяг определяется разницей между длиной пружины и длиной вытянутого штока. Т.е. это та часть значения х, которая сохраняется даже при подъеме авто на подъемнике. На само значение х преднатяг не влияет. Если говорят, что преднатяг нулевой, то это значит, что при разборе и сборе стойки Вам не понадобятся стяжки пружин.
Физика подвески и рулевого управления. Часть 1. Пружины
Начинаю новую рубрику записей, посвященную немаловажным узлам автомобиля — подвеска и рулевое управление. Если в Ваших планах нет изменения конструкции авто, то расчеты, которые мы будем здесь проводить, наврядли будут Вам полезны. Но вот если в планах доработка авто, то они придутся в самый раз.
Почему я решил начать данную рубрику? Потому что тюнинг авто необходимо начинать с подвески и тормозов. В большинстве случаев модернизация подвески производится методом перебора запчастей, что неслабо бьет по карману. Здесь я постараюсь рассмотреть задачи, которые помогут сэкономить время и деньги, тем самым получить желаемый результат.
Сегодня я напишу про такую простую деталь автомобиля как пружина подвески. Зачастую модернизация подвески начинается именно с этого узла. Почему? Ну, если спросить профессионального тюнера или гонщика, то он ответит, что это необходимо для настройки баланса автомобиля при торможении и в поворотах. Ну, а сели спросить владельца какой-нибудь заниженной Приоры, то, скорее всего, ответ будет: потому что круто смотрится=)
Итак, пружина подвески — это деталь, которая обеспечивает реакцию изменения клиренса на силовое воздействие дорожного покрытия или в результате маневров автомобиля. Кроме того, пружина с аммортизатором обеспечивают и стационарный клиренс.
Работает пружина просто: при воздействии некоторой силы происходит её сжатие на конкретную величину. Эта величина находится из закона Гука:
где х — это изменение длины,
F — действующая на пружину сила,
k — коэффициент жесткости.
В стационарном состоянии (т.е. когда авто не подвижен) силой является вес автомобиля. При развесовке автомобиля по осям 50/50 и наклоне оси пружины 0 градусов на каждую пружину действует сила, равная:
F = mg / 4,
где
m — масса автомобиля,
g — ускорение свободного падения.
Тут нужно отметить следующие моменты:
1. Развесовка 50/50 — это редкость
2. Нулевой наклон оси пружины — тоже редкость.
Тогда перепишем силу, действующую на реальную пружину подвески:
где
m — масса автомобиля,
g — ускорение свободного падения,
Y — коэффициент развесовки на данную ось (при развесовке 60 перед, 40 зад он будет равен 0,6 для передней пружины, 0,4 для задней),
а — угол наклона пружины.
Если же пружина работает в паре в газовым аммортизатором, то в стационарном состоянии на пружину действует меньшая сила:
F = mg * Y* cos(a) /2 — N,
где:
m — масса автомобиля,
g — ускорение свободного падения,
Y — коэффициент развесовки на данную ось (при развесовке 60 перед, 40 зад он будет равен 0,6 для передней пружины, 0,4 для задней),
а — угол наклона пружины,
N — сила реакции штока.
Теперь об изменении длины под действием силы. Как мы разобрались ранее данная величина находится из закона Гука:
Если с силами мы разобрались, то теперь поговорим о коэффициенте жесткости пружины. Для идеально цилиндрической пружины он равен:
k = G * d^4 / ( 8 * n * (D-d)^3 ),
где:
G — модуль сдвига (зависит от материала пружины),
d — диаметр прутка,
n — количество витков,
D — наружний диаметр пружины.
Какие выводы можно сделать?
1. Коэффициент жесткости не зависит от длины пружины, но зависит от количества витков, поэтому когда мы срезаем один или два витка, происходит увеличение коэффициента жесткости.
2. Увеличение толщины прутка на 10 процентов при тех же остальных параметрах дает увеличение коэффициента жесткости почти на 50 процентов. Это связано с тем, что коэффициент жесткости прямопропорционален диаметру прутка в четвертой степени.
3. Коэффициент жесткости зависит от материала, из которого сделана пружина.
Теперь поговорим о клиренсе в стационарном режиме. Клиренс определяется как раз изменением длины пружины под действием силы тяжести.
Если мы хотим сохранить клиренс, но ужесточить подвеску, нам необходимо изменить параметр х в сторону уменьшения за счет увеличения коэфициента жесткости, при этом на столько же, насколько изменили значение х, необходимо выбрать пружину короче. Если мы увеличим только жесткость, но при этом длина пружина останется прежней, авто станет жестче, но при этом приподнимется.
Если мы хотим приподнять машину, но сохранить жесткость, то необходимо использовать более длинные пружины, но с тем же коэффициентом жесткости. На чем хотелось бы сакцентировать внимание: если происходит изменение клиренса одной из осей, а клиренс второй оси остается прежний, то автоматически происходит изменение распределения веса по осям. Если мы приподняли заднюю часть, то баланс веса смещается вперед, соответственно, сила, действующая на задние пружины становится меньше, а значит и параметр х тоже уменьшается. Этот прием часто применяется для снижения вероятности пробуксовки передней оси на переднеприводных автомобилях. Наиболее популярный метод сохранения жесткости с увеличением клиренса — это установка проставок под те же пружины или на опорную чашку. При таком подходе сама пружина сжимается под весом авто почти так же, как и до доработки, с небольшой поправкой на перераспределение веса по осям, но за счет проставок дорожный просвет увеличивается на толщину проставки.
Параметр х очень важен для стойки, так как у штока аммортизатора имеется некоторый участок примерно в треть длины, который в стационарном состоянии должен находиться внутри аммортизатора. Это необходимо для того, чтобы аммортизатор работал не только на отбой, но и на разгрузку. Если Вы поставите пружины настолько жесткие, что после опускания автомобиля с домкрата пружина не сожмется на необходимый ход штока, то в процессе эксплуатации аммортизаторы очень быстро выйдут из строя. Кроме того, неправильно подобранное значение х повлияет и на управляемость автомобиля — неправильно настроенная ось будет подпрыгивать на каждой кочке и в поворотах.
Ну, и в заключение поговорим о понятии «преднатяг». Если пружина ставится соосно с аммортизатором, то преднатяг определяется разницей между длиной пружины и длиной вытянутого штока. Т.е. это та часть значения х, которая сохраняется даже при подъеме авто на подъемнике. На само значение х преднатяг не влияет. Если говорят, что преднатяг нулевой, то это значит, что при разборе и сборе стойки Вам не понадобятся стяжки пружин.
На сим все!
Аккуратнее экспериментируйте с ходовой частью;)
Герб Адамс — Разработка шасси. Глава 5. Пружины и амортизаторы (Часть 1)
ГЛАВА 5. ПРУЖИНЫ И АМОРТИЗАТОРЫ
Пружины и амортизаторы являются неотъемлемой частью подвески любого типа. Но общая система подвески должна рассматриваться как согласованный пакет, поэтому простая замена пружин и/или амортизаторов не всегда приведёт к желаемому результату. То, что работает на одном автомобиле, может не работать на другом автомобиле из-за различий в их конструкции. При выборе пружин и амортизаторов для вашего автомобиля следует учитывать следующие аспекты.
5.1 НАГРУЗКА ПРУЖИНЫ И ЕЁ ЖЁСТКОСТЬ
Пружинную нагрузку и жёсткость пружины часто путают. Для лучшего понимания того, как работает ваша подвеска, важно осознать эту разницу.
Нагрузка пружины — это величина веса, выраженная в кгс, которая потребуется для сжатия пружины на заданную высоту.
Жёсткость пружины — это величина веса, выраженная в кгс/см, которая потребуется, чтобы сжать пружину на один сантиметр (*т.е. это удельная пружинная нагрузка).
Пример этой взаимосвязи пружин приведен в табл. 5-1.
Табл. 5-1. Типичная задняя пружина
╔══════════════╦══════════════════╦═══════════════╗
║Сжатие пружины, см ║ Жёсткость пружины, кгс/см║ Нагрузка пружины, кгс║
║______________ 2.54║___________________ 26.8║_________________68║
║______________ 5.08║___________________ 26.8║________________136║
║______________ 7.62║___________________ 26.8║________________204║
║_____________ 10.16║___________________ 26.8║________________272║
║_____________ 12.70║___________________ 26.8║________________340║
║_____________ 15.24║___________________ 26.8║________________408║
║_____________ 17.78║___________________ 26.8║________________476║
║_____________ 20.32║___________________ 26.8║________________544║
╚══════════════╩══════════════════╩═══════════════╝
Обратите внимание, что при сжатии пружины её жёсткость не изменяется, а нагрузка — меняется. В табл. 5-1 на каждые 68 кгс нагрузки пружина сжимается на 2.54 см (1 дюйм). Жёсткость пружины определяет на сколько пружина будет сжиматься по мере увеличения нагрузки. Нагрузка пружины определяет сколько веса пружина может поддерживать на заданной высоте. Например, когда пружина сжимается на 17.78 см, она держит 476 кгс нагрузки. Если один из углов вашего автомобиля просел, то вам не нужна пружина бОльшей жёсткости, вам нужна пружина бОльшей нагрузки.
5.1.2 Жёсткость на колесе против жёсткости пружины
Эта взаимосвязь часто сбивает с толку, когда энтузиасты пытаются непосредственно измерить результаты. Жёсткость на колесе — это фактическая жёсткость пружины на колесе, а не жёсткость самой пружины. Это не простая взаимосвязь, поэтому добавление 17.8 кгс/см к жёсткости пружины не добавит 17.8 кгс/см к жёсткости на колесе, только если пружина не установлена непосредственно на оси. Всегда, когда есть связи, такие как задействованные рычаги подвески, вам необходимо учитывать коэффициенты передачи. Поскольку большинство современных автомобилей используют верхние и нижние рычаги на передней подвеске, мы воспользуемся этим примером, чтобы продемонстрировать как работают коэффициенты передачи. На рис. 5-1 показана схема типичной передней подвески с верхними и нижними рычагами подвески и пружиной, действующей на нижний рычаг. Формула для определения жёсткости на колесе:
Жёсткость на колесе = Жёсткость пружины × (A/B)² × (C/D)²,
где
A — расстояние от внутреннего шарнира нижнего рычага до центральной точки действия пружины;
B — расстояние от внутреннего шарнира нижнего рычага до его шаровой опоры;
C — расстояние от шаровой опоры нижнего рычага до мгновенного центра скоростей;
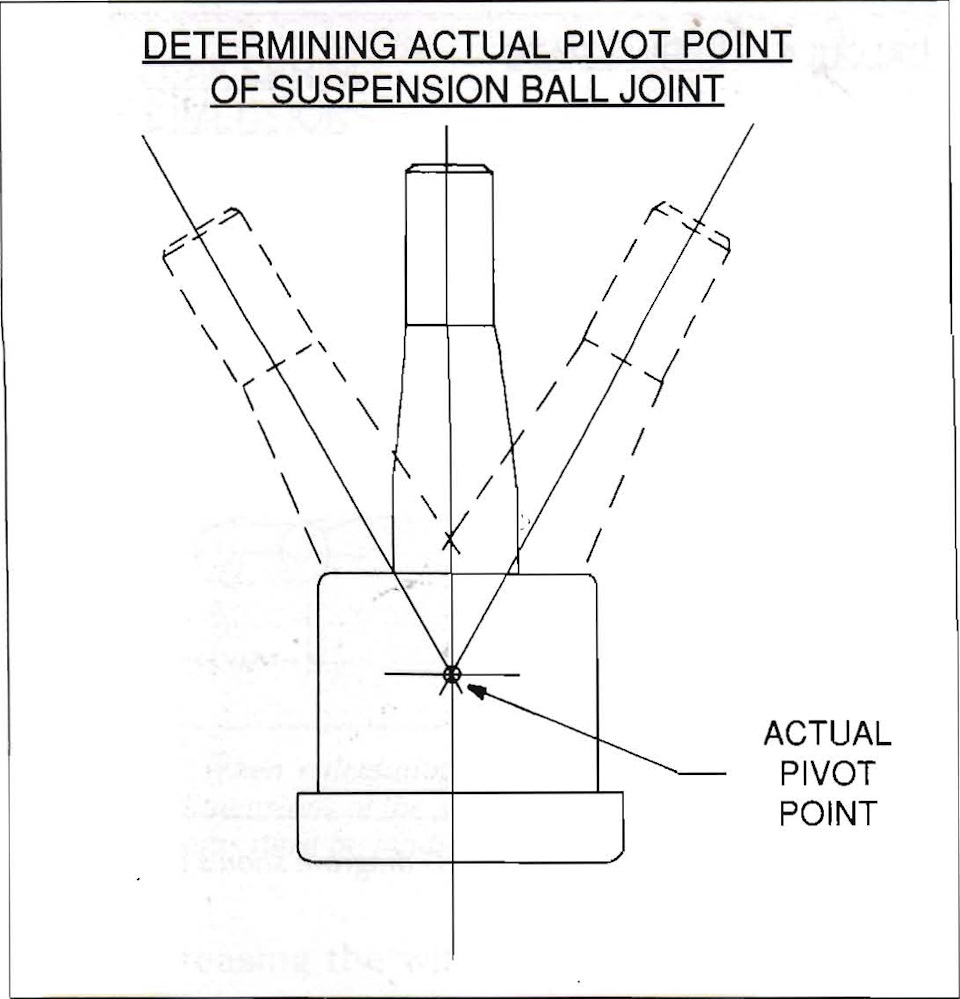
D — расстояние от середины пятна контакта шины до мгновенного центра скоростей.
Определение мгновенного центра скоростей. Чтобы точно найти мгновенный центр скоростей передней подвески, вам нужно сделать масштабный чертёж, основанный на измерениях, сделанных на автомобиле, установленном на ездовой высоте. Это звучит трудоёмко, но вы можете сделать это с рулеткой примерно за час. Чтобы получить достоверные результаты, нет необходимости измерять точнее 0.16 см. Однако, следует озаботиться определением фактической точки поворота шаровых опор. Её трудно определить, так как она находится внутри шарнира. Если у вас есть шаровая опора от автомобиля, то вы можете сдвинуть её из одного крайнего положения в другое и на глаз определить фактический центр вращения. Он обычно близок к фланцу или к концу корпуса, поэтому вы можете использовать его в качестве контрольной точки при проведении измерений на вашем автомобиле (рис. 5-2).
Когда вы сделаете схему своей передней подвески, у вас будут размеры A, B, C и D, необходимые для подстановки в уравнение жёсткости на колесе. В целях дальнейшего пояснения предположим, что вы имеете следующие размеры:
A = 22.86 см
B = 35.46 см
C = 228.6 см
D = 238.76 см
Если эти размеры подставить в формулу, то с пружиной жёсткостью 89.29 кгс/см получатся следующие результаты:
Жёсткость на колесе = 89.29 × (22.86/35.46)² × (228.6/238.76)² ≈ 33.83 кгс/см
Обратите внимание, что при такой конфигурации жёсткость на колесе составляет 37.9% от жёсткости пружины. Это означает, что добавление 10 кгс/см к жёсткости пружины добавит лишь 3.79 кгс/см к жёсткости на колесе.
Используя этот же пример, давайте посмотрим, что произойдёт когда крепление пружины на нижнем рычаге подвески сдвинется на 2.54 см наружу:
A = 25.4 см
B = 35.46 см
C = 228.6 см
D = 238.76 см
Жёсткость на колесе = 89.29 × (25.4/35.46)² × (228.6/238.76)² ≈ 41.76 кгс/см
Эта жёсткость на колесе составляет около 46.77% от жёсткости пружины, поэтому перемещение точки крепления пружины на 2.54 см наружу увеличивает жёсткость на колесе больше, чем добавление 10 кгс/см к жёсткости пружины.
Из-за влияния коэффициентов передачи, как правило, невозможно сравнивать жёсткости пружин одного автомобиля с жёсткостями пружин другого автомобиля, только если не известны размеры всех связей. Из приведенных выше примеров также очевидно, что простое использование колёс с бОльшим или меньшим вылетом будет иметь некоторое влияние на фактическую жёсткость на колесе (*уменьшение ET приводит к уменьшению жёсткости на колесе).
5.1.3 Расчёт жёсткости винтовых пружин
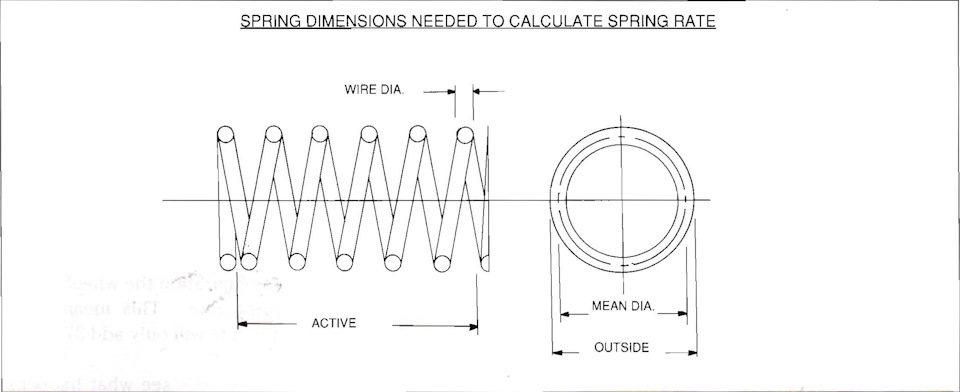
Если у вас есть доступ к измерителю жёсткости пружин, то вы можете измерить жёсткость всех ваших пружин. Если у вас нет измерителя жёсткости, то вы также можете определить жёсткость ваших пружин, сняв их размеры и воспользовавшись следующей формулой:
Жёсткость винтовой пружины = G(d²)²/(8ND³),
где
G — модуль сдвига материала пружины, для стали 79300 МПа;
d — диаметр прутка пружины, мм;
N — число рабочих витков;
D — срединный диаметр витков, мм.
Коэффициент G в уравнении для цилиндрических пружин, изготовленных из стали, всегда один и тот же. Для титановых пружин потребуется другой коэффициент (*41400 МПа, титан мягче).
Диаметр прутка пружины d можно измерить с помощью штангенциркуля. Он будет одинаков по всей длине пружины, только если это не пружина переменной жёсткости, и в этом случае вы не можете подставить этот размер в формулу. Для нашего примера мы предположим, что диаметр прутка составляет 15.75 мм.
Определение количества активных витков требует определённого решения с вашей стороны. Механическая обработка играет роль. Если концы пружины сплющены или механически обработаны, то эти витки неактивны, так как они покоятся на своих монтажных площадках. При подсчёте действующих витков учитывайте только те, которые могут перемещаться по мере сжатия пружины. Предположим, например, что пружина имеет 10 активных витков.
Определение срединного диаметра пружины можно выполнить с помощью рулетки, начиная с конца пружины, как показано на рис. 5-3. В нашем примере мы предположим, что срединный диаметр витка составляет 127 мм. Подставляя в формулу эти размеры, получим:
Жёсткость винтовой пружины = 79300∙(15.75²)²/(8∙10∙127³) ≈ 29.78 кгс/см.
Из этого расчёта следует отметить несколько вещей.
1. Если мы срежем один виток пружины, то у неё будет меньше активных витков, длина пружины изменится, а жёсткость будет увеличена:
Жёсткость винтовой пружины = 79300∙(15.75²)²/(8∙9∙127³) ≈ 33.09 кгс/см.
Это примерно на 11% больше, что пропорционально количеству срезанных витков.
2. Увеличение диаметра прутка приведёт к резкому увеличению жёсткости пружины. Если мы увеличим диаметр прутка только на 0.8 мм, то жёсткость пружины будет равна
Жёсткость винтовой пружины = 79300∙(16.55²)²/(8∙9∙127³) ≈ 40.34 кгс/см.
3. Ничто в расчёте жёсткости пружины не указывает на то, что винтовая пружина когда-либо меняет свою жёсткость. Жёсткость определяется материалом (сталью в нашем случае) и размерами пружины. Винтовые пружины не изнашиваются и не теряют жёсткость.
4. Ничто в расчёте жёсткости пружины не описывает пружинную нагрузку. Пружинная нагрузка определяет, сколько веса пружина может поддерживать на заданной высоте. Жёсткость пружины указывает только то, насколько изменится высота при изменении нагрузки. Пружина может потерять свою нагрузку с течением времени (*релаксировать) или если сталь не подвергалась термообработке должным образом. Тем не менее, когда пружина проседает, её жёсткость остаётся такой же, как когда она была новой.
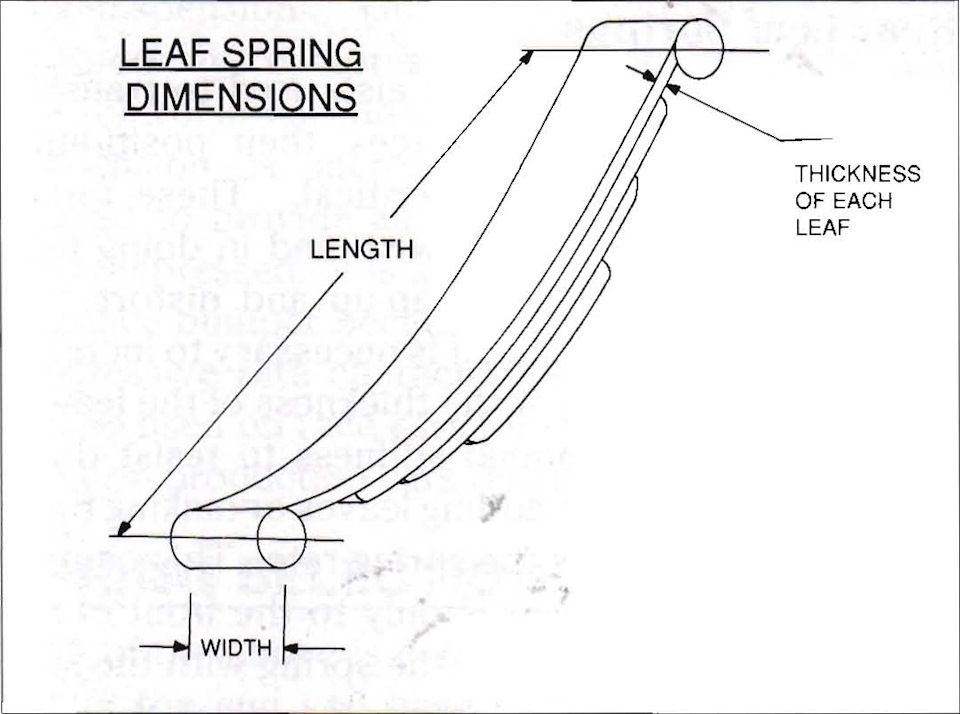
5.1.4 Расчёт жёсткости листовых рессор
Жёсткость листовой рессоры (*пластинчатой пружины) определяется её физическими размерами, как показано на рис. 5-4. Жёсткость листовой рессоры может быть аппроксимирована следующей формулой:
Жёсткость листовой рессоры = (WN/12) × (1000∙t/L)³,
где
W — ширина листов, мм;
N — число листов;
t — толщина одного листа, мм;
L — длина пружины, мм.
В качестве примера предположим следующие размеры:
W = 7.62 см;
N = 5;
t = 0.635 см;
L = 152.4 см.
Подстановка этих значений в формулу приводит к:
Жёсткость листовой рессоры = (W∙5/12) × (1000∙0.635/152.4)³ ≈ кгс/см.
5.2 ГДЕ УСТАНАВЛИВАТЬ ПРУЖИНЫ
Места установки пружин так же важны, как и их жёсткости. Эти факторы надо учитывать как на существующем автомобиле, так и на вновь проектируемом.
5.2.1 Передние пружины
Чтобы свести к минимуму влияние коэффициента передачи, обычно передние пружины лучше всего монтировать как можно ближе к шаровой опоре. Существуют очевидные соображения о допустимости монтажа, который должен быть разрешим, но в целом, чем ближе, тем лучше. На автомобилях Winston Cup, которые всё ещё используют пятидюймовые пружины, невозможно установить пружины очень близко к шаровой опоре. Это приводит к большому передаточному коэффициенту и потребности в пружинах очень высокой жёсткости. Также хорошей политикой является крепление пружин в как можно более вертикальном положении, чтобы иметь силу пружины в её полном объёме.
5.2.2 Задние винтовые пружины
Часто имеется возможность устанавливать задние винтовые пружины непосредственно на корпусе оси. Такая конфигурация создаёт жёсткость на колесе, равную жёсткости пружины. Задние пружины также могут быть установлены на задних рычагах подвески, но, поскольку это приводит к рассмотрению коэффициента передачи, жёсткость на колесе уже не будет такой же, как жёсткость пружины.
При установке задних пружин также необходимо учитывать угол наклона пружин относительно вертикали, так как этот угол может влиять на фактическую силу пружины. Установка пружин под углом к вертикали может уменьшить эффективное усилие, которое пружина обеспечивает в вертикальном направлении. Небольшое отклонение имеет небольшой влияние, но угол более 30° приведёт к значительному уменьшению вертикальной силы на оси и, соответственно, уменьшению эффективности пружины.
5.2.3 Задние листовые рессоры
Поскольку задние листовые рессоры используются также для передачи ускоряющих и тормозных усилий, их местоположение и форма являются более критичными. Эти силы заставляют корпус оси закручиваться, и при этом листовые рессоры имеют тенденцию к скручиванию и искажению. Чтобы противодействовать такому состоянию, необходимо увеличить количество листов или их толщину, чтобы дать рессоре достаточную угловую жёсткость для противостояния этим силам. К сожалению, добавление листов или их толщины увеличивает жёсткость рессоры в целом. Это противоречие решается путём добавления листов только к передней части рессоры, что даёт рессоре жёсткость в её передней половине, необходимой для противодействия реакции от крутящего момента на оси, при этом не увеличивая вертикальную жёсткость пружины в той мере, как если бы был добавлен полный лист. Именно по этой причине большинство листовых рессор, используемых на гоночных автомобилях, имеют дополнительные листы только на своей передней части.
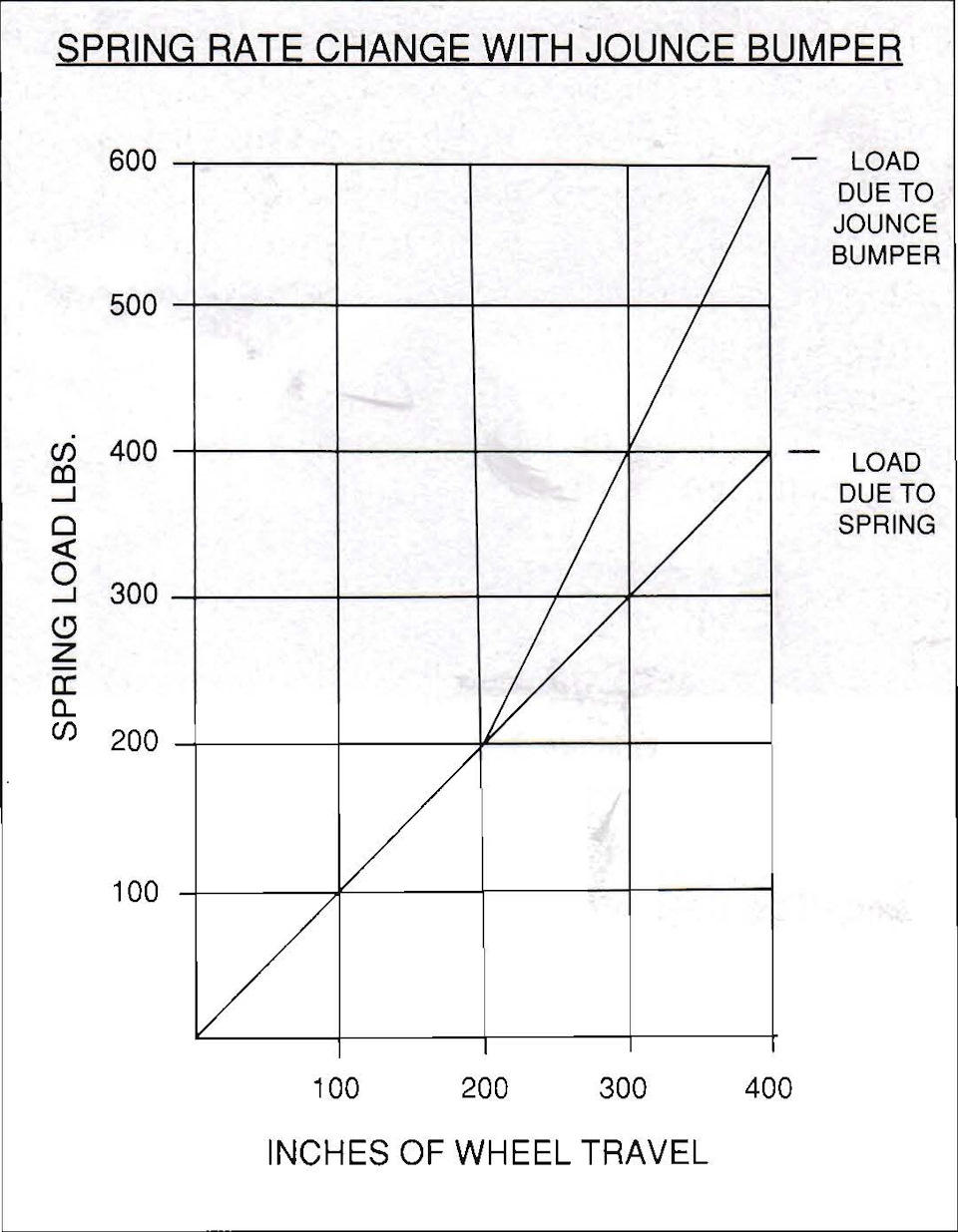
5.3 ОГРАНИЧИТЕЛИ ХОДА ПОДВЕСКИ
Ограничители хода подвески (буферы-отбойники) — это резиновые блоки, которые удерживают нижние рычаги подвески от удара о раму или кузов при сильных толчках. Многие энтузиасты выбрасывают их, что является ошибкой, поскольку они не осознают, что эти буферы в действительности являются пружинами переменной жёсткости. Используя буферы-отбойники, становится возможным использование более мягких пружин. В свободном ходе перед тем, как отбойники касаются рамы или кузова, только автомобильные пружины являются активными элементами подвески. При сильных ударах буферы-отбойники сжимаются между рамой и рычагами подвески, при этом эффективная жёсткость пружины увеличивается. Буферы-отбойники имеют форму, обеспечивающую всё возрастающую жёсткость по мере их сжатия. Ошибочно обрезать форму буфера-отбойника, поскольку это разрушает его прогрессивную характеристику жёсткости. Буферы-отбойники могут использоваться на гоночных автомобилях по тем же причинам, по которым они используются на серийных автомобилях (рис. 5-5).
5.4 ВЫБОР ПРУЖИН
Всё вышесказанное является хорошей справочной информацией, но в конце концов вы должны принять решение о том, какие пружины использовать на своём автомобиле. Понимание всех задействованных факторов поможет принять это решение, а также поможет рационализировать пружины, которые вы уже используете. Ниже приведены некоторые из факторов, которые следует учитывать при выборе пружин для вашего автомобиля.
5.4.1 Аэродинамические эффекты
Некоторые гоночные автомобили, такие как Indycar, могут иметь аэродинамическую прижимную силу, превышающую вес автомобиля. Если у вас 1360 кг автомобиль с 1360 кгс прижимной силы, то вам потребуются жёсткость и нагрузка пружины вдвое большие, чем при нулевой аэродинамической прижимной силе. Заводской автомобильный кузов на треке длиной 1/4 мили не имеет большой аэродинамической прижимной силы, но некоторые модифицированные автомобили имеют её значительную величину.
5.4.2 Жёсткость пружин слева и справа
Автомобили, используемые на круговых трассах, имеют большой процент веса, переносимого во время поворота на правый борт. Поскольку эффективный вес с правой стороны автомобиля увеличивается, там потребуется пружина бОльшей жёсткости и нагрузки. Установка более мягких пружин с левой стороны является популярным выбором, поскольку это не нарушает общий баланс автомобиля. Скоростные дорожные и уличные автомобили обычно используют пружины одних и тех же жёсткостей и нагрузок с левой и правой стороны, потому что они испытывают как левый, так и правый повороты.
5.4.3 Эффекты от слишком жёстких пружин
Так как большинство гоночных автомобилей могут регулировать пружинную нагрузку для установки правильной ездовой высоты, выбор наилучшей жёсткости пружины обычно вызывает наибольшую озабоченность у гонщиков. Мы обсудили причины, по которым может потребоваться бОльшая жёсткость пружин, но как узнать не слишком ли жёсткие у вас пружины? Как правило, лучше всего использовать как можно более мягкую пружину. Сцепление между автомобильными шинами и дорогой является единственным источником развития поворачивающей силы. Если шины теряют контакт с дорогой, то они создают нулевую силу для поворота. Мягкие пружины позволяют шинам лучше следить за дорожными ухабами и неровностями, поэтому шины остаются в контакте с дорогой в течение большего процента времени. Более высокая жёсткость пружины также может ограничить ход подвески как на сжатие, так и на отбой. Если ваш автомобиль не получает полного хода подвески, то, возможно, это не позволит шинам следовать по дороге в максимально возможной степени.
Пружины переменной жёсткости. Изучение оптимальных жёсткостей пружин для автомобиля в конечном итоге приводит к выводу, что наилучшая жёсткость пружины является переменной величиной. Мы хотели бы иметь мягкую пружину, чтобы поглощать дорожные неровности, а затем иметь высокую жёсткость пружины, чтобы поглощать большие удары. Имеются пружины, которые изготовлены с переменной жёсткостью. Вы можете определить эти пружины, заметив, что расстояние между витками отличается от одного конца к другому. Конструкторское решение для этих пружин верное, но на практике они не работают слишком хорошо. Поскольку автомобильные пружины работают только в ограниченной части от общего хода подвески, величина изменения в их жёсткости обычно довольно мала. Буферы-отбойники обеспечивают такую же функцию переменной жёсткости, но с большей согласованностью.
5.4.4 Жёсткость пружин для овальных трасс
Когда автомобиль движется по овальной трассе с наклоном, жёсткость пружин должна быть увеличена, дабы компенсировать увеличение эффективного веса автомобиля. В табл. 5-2 приведены приблизительные значения процента увеличения жёсткости пружин для разных углов наклона трасс. Эти расчёты выполнены для автомобиля, испытывающего перегрузку 1 на поворотах для всех углов наклона трассы. Поскольку автомобиль может не поддерживать такую перегрузку в поворотах из-за аэродинамики или мощности, эти цифры могут быть завышенными при некоторых обстоятельствах. Эти значения близки, но автомобиль и водитель должны быть последними элементами при выборе жёсткости пружин на любом заданном треке.
Табл. 5-2.
╔═══════════════╦════════════════════════╗
║Угол наклона трассы, °║Приращение жёсткости пружины, % ║
║__________________0║_____________________________ 0║
║__________________5║____________________________ 10║
║_________________10║____________________________ 23║
║_________________15║____________________________ 41║
║_________________20║____________________________ 67║
║_________________25║___________________________ 106║
╚═══════════════╩════════════════════════╝
5.4.5 Жёсткость пружин для уличного применения
Цель пружин подвески — удерживать автомобиль в спокойном состоянии, при этом позволяя колёсам отслеживать неровности дороги. В общем, самые мягкие пружины будут делать эту работу лучше всего. Более мягкие пружины позволяют каждому отдельному колесу перемещаться относительно шасси при минимальном воздействии на кабину водителя. Это приводит к мягкой езде, шумоизоляции и хорошей управляемости.
Более жёсткие пружины делают езду автомобиля жёсткой. У них нет возможности значительно улучшить управляемость. До тех пор, пока пружины на автомобиле достаточно жёсткие для того, чтобы автомобиль не цеплял днищем, они адекватны. Если автомобиль занижен, то небольшое увеличение жёсткости пружин может быть использовано для компенсации уменьшенного хода подвески.
Некоторые автомобильные энтузиасты ошибочно полагают, что если пружины жёсткостью 20 кгс/см хороши, то пружины жёсткостью 40 кгс/см должны быть ещё лучше. Они ошибаются. Оптимальное сцепление с дорогой требует, чтобы шины находились в контакте с дорожным покрытием; мягкая пружина позволяет колёсам отслеживать неровности дороги, так что шины могут создавать максимальное сцепление.
Наша рекомендация для передних пружин на уличных автомобилях — использовать стандартные заводские пружины. Чтобы немного опустить автомобиль для уличного использования, вы можете отрезать одну половину витка с верхней части пружины, используя ацетиленовую горелку.
Большинство передних пружин имеют жёсткость от 50 до 60 кгс/см. Обрезка витка, как мы рекомендовали, увеличит жёсткость примерно на 10%. Но истинная цель обрезки передних пружин — занизить автомобиль для улучшения аэродинамики и управляемости, а не для увеличения жёсткости пружины.
Некоторые автомобили, таких как Corvette с подвеской F-41, Pontiac WS-6 Trans Am и более поздняя модель Chevrolet Camaro Z-28, оснащены очень жёсткими пружинами. Мы обнаружили, что езда может быть значительно улучшена за счёт установки более мягких пружин, не влияя на возможности управляемости этих автомобилей. Многие энтузиасты покупают для этих автомобилей стандартные мягкие пружины у своего дилера и отрезают 1/2 витка для правильной ездовой высоты.