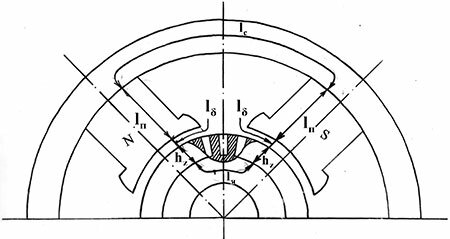
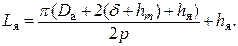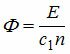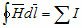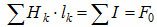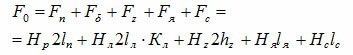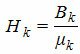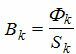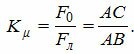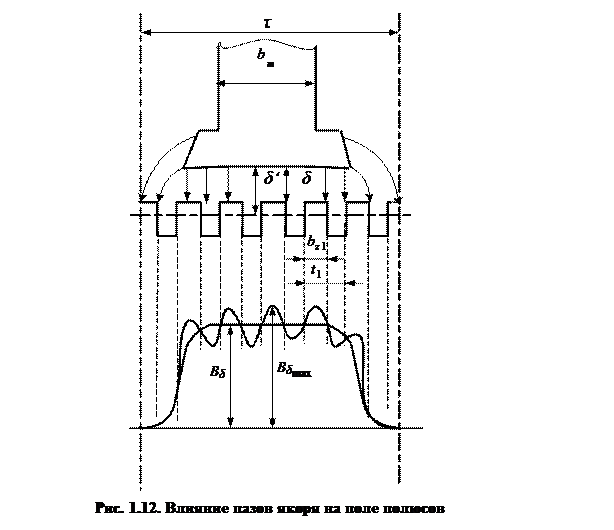Расчетный участок магнитной цепи четырехполюсной машины постоянного тока
Магнитная цепь машины постоянного тока
Магнитная система машины постоянного тока состоит из станины (ярма), сердечников главных полюсов с полюсными наконечниками, воздушного зазора и сердечника якоря.
На рис. 26.1 показана картина магнитного поля четырехполюсной машины. При этом имеется в виду V машина, работающая в режиме х. х., когда МДС создается лишь обмоткой возбуждения, а в обмотке якоря и обмотке добавочных полюсов тока нет или он настолько мал, что его влиянием на картину магнитного поля можно пренебречь. В целях упрощения на рисунке не показаны добавочные полюсы, так как в режиме х. х. их влияние на картину магнитного поля машины незначительно. Как это следует из рис. 26.1, магнитный поток главных полюсов состоит из двух неравных частей: большая часть образует основной магнитный поток Ф, а меньшая — магнитный поток рассеяния полюсов Ф„. Поток рассеяния учитывается коэффициентом рассеяния от (см. § 20.1).
Магнитодвижущая сила обмотки возбуждения на пару полюсов в режиме х.х. определяется суммой магнитных напряжений на участках магнитной цепи (рис. 26.2):
Fво= ∑F=2Fδ + 2Fz + 2Fm + 2Fa + Fя, (26.1)
где Fδ, Fz, Fm, Fa, Fя — магнитные напряжения воздушного зазора, зубцового слоя якоря, главного полюса, спинки якоря, станины (ярма) соответственно.
Если машина имеет компенсационную обмотку (см. § 26.4), то в (26.1) следует ввести еще одно слагаемое Fzm, представляющее собой магнитное напряжение зубцового слоя главного полюса.
Порядок расчета магнитных напряжений на участках магнитной цепи машины постоянного тока в принципе такой же, что и в случае асинхронной машины (см. гл. 11). При этом расчет магнитных
напряжений станины и сердечника главного полюса ведут по магнитному потоку главного полюса Фт, который больше основного потока Ф на значение потока рассеяния Фа:
где σm≈10δ/τ = 0,10-0,25 — коэффициент рассеяния.
Рис. 26.1. Магнитное поле машины постоянного тока в режиме х.х.
При заданном значении ЭДС машины Еа определяют требуемое значение основного магнитного потока (Вб) [см. (25.20)]:
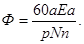
Рис. 26.2. Расчетный участок магнитной цепи четырехполюсной машины постоянного тока
Далее рассчитывают магнитную индукцию для каждого участка магнитной цепи:
По таблицам или кривым намагничивания для соответствующих ферромагнитных материалов находят напряженность магнитного поля на участках магнитной цепи Нх, а затем определяют магнитное напряжение (А)
Другие участки магнитной цепи выполняют из ферромагнитных материалов. В машинах постоянного тока для изготовления различных элементов магнитной цепи применяют следующие материалы.
Сердечник якоря — тонколистовые электротехнические стали марок 2013, 2312 и 2411 толщиной 0,5 мм (см. табл. 11.1).
Сердечник главного полюса — листовая анизотропная (холоднокатаная) сталь марки 3411 толщиной 1 мм, пластины не изолируют.
Станина — в машинах малой мощности станину изготовляют из стальных цельнотянутых труб, а для машин средней, и большой мощности станины делают сварными из листовой^ конструкционной стали марки СтЗ.
Магнитное напряжение воздушного зазора (А)
где δ — величина воздушного зазора, мм; — коэффициент воздушного зазора, учитывающий увеличение магнитного’ сопротивления зазора из-за зубчатости якоря (kδ>1).
Магнитная индукция в воздушном зазоре Вδ (Тл) пропорциональна основному магнитному потоку Ф. В машинах постоянного тока общего назначения Вδ = 0,6-1,0 Тл (большие значения Вδ, соответствуют более крупным машинам).
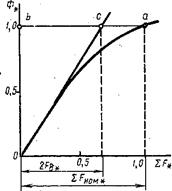
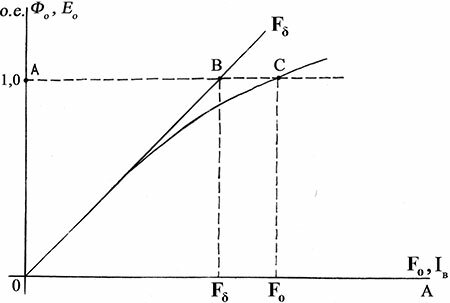
Обычно расчет МДС ∑F ведут для ряда значений магнитного потока (0,5Фном, 0,75Фном, Фном и 1,2 Фном), а затем строят магнитную характеристику машины Ф* = f(∑F*), где Ф* =Ф/Фном — относительное значение магнитного потока; ∑F* = ∑F/ ∑ZFном — относительное значение МДС обмотки возбуждения на пару полюсов в режиме х. х.; Фном и ∑Fном — номинальные значения магнитного потока и МДС в режиме х. х., соответствующие номинальному значению ЭДС Еа [см. (26.2) ]. В начальной части магнитная характеристика прямолинейна (рис. 26.3). Объясняется это тем, что при небольших значениях ∑F* магнитная цепь не насыщена и МДС возбуждения определяется, в основном, магнитным напряжением воздушного зазора ∑F≈2Fδ.Затем с ростом 2F*
наступает насыщение магнитной цепи и магнитная характеристика становится криволинейной. Коэффициент насыщения магнитной цепи машины
kμ = ∑Fном*/(2Fδ*) = ba/bc = 1/(2Fδ*) (26.5)
Магнитная цепь машины постоянного тока
Для получения в машине постоянного тока номинальных данных в ней необходимо наличие магнитного потока Ф. Требуемая величина магнитного потока может быть определена из формулы
Магнитный поток в машинах постоянного тока создается под действием
Рис. 1 — Магнитная цепь пары полюсов четырехполюсной машины
магнитодвижущей силы (МДС) обмоток возбуждения главных полюсов. Магнитный поток замыкается в машине между разноименными полюсами по определенному пути, который называется магнитной цепью машины.На рисунке 1.25 показана магнитная цепь пары полюсов четырехполюсной машины. Магнитная цепь машины обычно симметрична и имеет пять характерных однородных участков: главные полюса hп, воздушный зазор ?, зубцы якоря hz, сердечник якоря lя и станину lc машины. Поток, создаваемый каждым из полюсов,, делится относительно продольной оси полюса на две части, образующие вместе с соседними полюсами два одинаковых магнитных контура. Число таких контуров равно числу полюсов. Расчет магнитной цепи машины постоянного тока заключается в определении МДС, необходимой для создания под полюсами машины основного магнитного потока требуемой величины. Расчет ведут обычно на одну пару полюсов ввиду симметричности машины. Магнитную цепь можно рассчитать на основе закона полного тока для средней магнитной линии
где 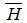
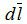
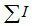
Предположив, что на протяжении каждого однородного участка Н постоянна, заменяем интеграл суммой
где Hk– напряженность магнитного поля в каждом однородном участке;
lk – средняя длина однородного участка;
F0 – полная МДС пары полюсов, действующая в контуре цепи.
Таким образом, общую МДС, действующую в контуре, можно представить суммой МДС, необходимых для проведения магнитного потока на заданных участках
Коэффициент K? учитывает возрастание среднего воздушного зазора, называется коэффициентом воздушного зазора (коэффициентом Картера) и равен 1,1?1,5. Величину напряженности поля в K–ом участке можно определить по формуле
где Bk – индукция магнитного поля в участке;
?k – магнитная проницаемость участка.
Для участков из ферромагнитных материалов Нk находится по кривым намагничивания В = f(H), так как для них ? = var.
Индукцию Bk определяют по величине потока Фk и сечению участка Sk
Эта зависимость (рис.2) носит название характеристики намагничивания машины. Степень насыщения магнитной системы машины характеризуется коэффициентом насыщения, который находится расчетным путем или из кривой намагничивания
Магнитная и электрическая цепи машин постоянного тока
Магнитная цепь машины предназначена для создания и распределения магнитного поля в воздушном зазоре и состоит из главных полюсов, сердечника якоря, воздушного зазора между полюсами и якорем и ярма (станины). В зависимости от числа главных полюсов магнитная система может быть двух- (рис. 1.1), четырех-(рис. 1.6), шестиполюсной и т.д. Пути магнитного потока для четырехполюсной машины показаны на рис. 1.6.
Распределение магнитной индукции в рабочем воздушном зазоре характеризуется кривой В (α) (рис. 1.7), где α – дуга окружности якоря (на рис. 1.7 магнитная система развернута в плоскость). Почти постоянное значение индукции В в воздушном зазоре необходимо для получения примерно постоянной ЭДС в проводниках, находящихся под полюсом, и оно обеспечивается специальной формой полюсных наконечников.
Линии симметрии m, n, делящие пространство между полюсами пополам, называются геометрическими нейтральными линиями, а линии, проходящие через точки, где В = 0, — физическими нейтральными линиями (в данном случае геометрическая и физическая нейтральные линии совпадают). Дуга между соседними нейтральными линиями называется полюсным делением. Она обозначается буквой τ и может выражаться в метрах, градусах, радианах, числе пазов и в других удобных для расчета единицах.
Электрическая цепь машины состоит из обмотки якоря, коллектора и щеток. Как указывалось, проводники якоря, соединяясь через коллекторные пластины, образуют замкнутую цепь. При вращении якоря по часовой стрелке проводники обмотки якоря пересекают магнитное поле полюсов и в них наводится переменная ЭДС: в верхней половине обмотки ЭДС направлены от нас, в нижней – к нам.

В обмотке якоря относительно внешней цепи образуются две параллельные ветви, ЭДС которых равны и которые во внешней цепи действуют согласно. При вращении якоря картина распределения ЭДС не изменяется, меняются только номера проводников, входящих в параллельные ветви. Разность потенциалов между щетками остается практически постоянной (если пренебречь небольшими пульсациямии ЭДС).
Замкнутую обмотку якоря можно получить двумя способами: соединять на коллекторе проводники обмотки двигаясь вперед – назад, т.е. возвращаясь назад к соседнему проводнику (рис. 1.9, а), или только вперед, обходя проводники якоря, двигаясь все время в одном направлении (рис. 1.9,б). Очевидно, что в любом случае каждый следующий проводник должен находится под полюсом противоположной полярности.
Это означает, что шаг обмотки близок к полюсному делению τ. В первом случае получаем так называемую петлевую обмотку, во втором – волновую обмотку.
В петлевых обмотках при числе полюсов больше двух (6, 8 и т.д.) число параллельных ветвей и щеток равно числу полюсов. В волновых обмотках число параллельных ветвей и щеток вне зависимости от числа полюсов равно двум.
Магнитная цепь машины постоянного тока
Магнитопровод – деталь электрических машин, предназначенная для усиления потока магнитной индукции на определенных участках магнитного поля. Магнитопровод машин и аппаратов с переменным или пульсирующим магнитным полем изготавливается из тонких изолированных стальных листов для уменьшения потерь из-за токов Фуко.
Магнитная цепь – это путь, по которому замыкаются магнитные силовые линии основного магнитного потока.
Основной магнитный поток Фδ – это поток в зазоре δ, приходящийся на один главный полюс машины и проходящий из статора в ротор. Величинаосновного магнитного потока определяет величину индуктируемой в обмотке якоря ЭДС. Магнитная цепь ЭМПТ симметрична. Рассмотрим её на пару полюсов. Магнитная цепь машины постоянного тока приведена на рисунке 1.10.
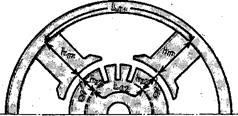
Рис. 1.10. Магнитная цепь ЭМПТ:
ha – высота спинки якоря;
hz – высота зубца ( паза) якоря;
δ – воздушный зазор;
Dа – наружный диаметр ротора;
Фδ – основной магнитный поток;
iв – ток обмотки возбуждения;
Часть потока, создаваемого полюсами, не проникает из статора в ротор через зазор, а рассеивается непосредственно вокруг обмотки возбуждения, называется потоком рассеяния – Фσ.
Тогда полный поток, созданный полюсами, будет:
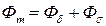

где кσ – коэффициент рассеяния полюса:
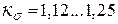
1.4.1. Расчёт магнитной цепи ЭМПТ
Магнитная цепь ЭМПТ рассчитывается в режиме холостого хода, т.е. ток якоря Ia = 0.
В основе расчёта лежит закон полного тока:
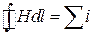
где Н – напряжённость магнитного поля;
dl – элемент длины магнитной силовой линии;
∑i – полный ток, охватываемый магнитной линией.
При расчёте магнитную цепь ЭМПТ разбивают на пять участков. Каждый участок по всей своей длине имеет одинаковое сечение, одинаковое значение магнитной индукции и одинаковую магнитную проницаемость, т.е. на всём протяжении участка напряжённость магнитного поля (Н = const):
1) воздушный зазор – δ;
Тогда по (1.11) запишем:
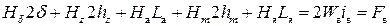
Здесь Fв – МДС возбуждения.
Поверочный расчёт магнитной цепи заключается в определении МДС возбуждения по заданным номинальным данным машины (Рн, nн, Uн, ηн, Iaн).
1. Приведём расчёт МДС магнитного зазора.
Рассмотрим ЭМПТ в пределах полюсного деления τ (рис. 1.11). При этом предположим, что якорь гладкий, т.е. пазы и зубцы отсутствуют.
Тогда магнитная индукция на протяжении полюсного деления распределяется по трапецеидальному закону (рис. 1.11, а), и индукция по длине машины распределяется также по трапецеидальному закону, максимальна и одинакова под полюсом, и поле ослабляется до нуля к торцам якоря (рис. 1.11, б).
На рис. 1.11, lа, lm – длины сердечников якоря и полюса соответственно. Тогда расчётная длина якоря lб находится при замене трапецеидальной кривой магнитного поля по длине машины (рис. 1.11,б) равновеликим по площади прямоугольником с основанием lб и высотой Вб:
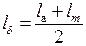
Расчётная длина полюсной дуги bб находится при замене трапецеидальной
кривой магнитного поля в пределах полюсного деления (рис. 1.11,а) равновеликим по площади прямоугольником с основанием bб и высотой Вб:

где αδ – коэффициент полюсной дуги, αδ = 0,6…0,85
Тогда определим магнитную индукцию в зазоре:

После расчёта номинальной магнитной индукции в зазоре, необходимо сверить полученной значение с рекомендуемыми:

Затем рассчитывается напряжённость магнитного поля в воздушном зазоре:

где 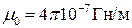
Тогда МДС воздушного зазора на пару полюсов при гладком якоре:

Но при наличии на якоре пазов, поле под ними ослабляется, и кривая поля в этом случае приобретает зубчатый вид (рис. 1.12).
Наличие пазов приводит к увеличению воздушного зазора, при этом вводят понятие эквивалентного воздушного зазора, который определяется как:
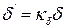
Здесь 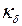
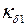
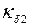
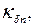
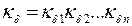
Пусть 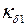
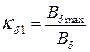
Коэффициент 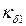

где t1 – зубцовое деление; 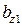
Найденное значение 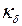

Тогда МДС воздушного зазора при учёте неравномерности зазора на пару полюсов:

2. Приведём расчёт МДС пазово-зубцовой зоны.
Расчёт пазово-зубцовой зоны производят на одно пазовое деление 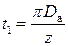
Возьмём произвольное сечение на расстоянии х от низа паза (рис. 1.13). Тогда магнитный поток, приходящийся на одно пазовое деление:

Этот поток делится на поток, проходящий через зубец, и поток, проходящий через паз:
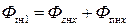
Разделим обе части последнего выражения на сечение зубца (на расстоянии х от низа паза):

а второе слагаемое правой части помножим и разделим на сечение паза (на расстоянии х от основания паза):
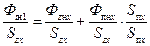

где 
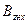


Тогда в сечениях 1,3, и среднем сечении, магнитная индукция будет:

При расчёте 
Здесь 

где nк, bк – число и ширина вентиляционных радиальных каналов (рис. 1.14).
Если магнитная индукция в данном сечении зубца, например, в сечении х, 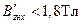

Затем по основной кривой намагничивания 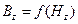

Если магнитная индукция в данном сечении зубца 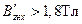

и напряжённость поля в данном сечении 

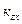
Таким образом, определили напряжённость поля в 3-х сечениях зубца 
По формуле Симпсона определим усреднённое значение 
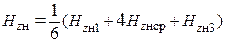
Тогда МДС зубцовой зоны на пару полюсов:

3. Приведём расчёт МДС спинки якоря.
Определим магнитную индукцию в спинке якоря:

Затем по основной кривой намагничивания 
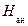
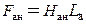
Здесь 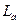
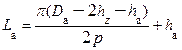
4. Приведём расчёт МДС полюса.
Определим магнитную индукцию в сердечнике полюса:
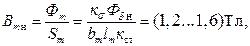
где кσ – коэффициент рассеяния полюса, 
Затем по кривой намагничивания 


5. Приведём расчёт МДС ярма.
Определим магнитную индукцию в ярме:

Затем по основной кривой намагничивания 

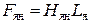
Здесь