Машина тьюринга возведение в квадрат
Машина Тьюринга. Записать все квадраты чисел, не превосходящих m≥1
Добрый день.
Задали задание на часть курсовой работы. :
Записать все квадраты чисел, не превосходящих m≥1
Ни каких разьяснений конечно же не дали. Какие числа, что к чему вообще. В задание нужно решить 2 способами. 1 построить программу с табличкой(Ну это вопрос кодирования. Это меня пока не волнует.). И второй способ вручную. Тоесть написать как переключается головка выполняя эту задачу.
П.С. Спасайте Выручайте.
Напечатать в строку квадраты всех целых чисел от 10 до b (значение b вводится с клавиатуры; b≥10)
1)Напечатать в строку квадраты всех целых чисел от 10 до b (значение b вводится с клавиатуры;.

Нужно помощь с алгоритмом Дано двоичное число. Справа через пробел записать цифры числа в обратном.
Составить программу-генератор простых чисел, в основу положить формулу 2*(x)^2 + 29 при 0 ≥ х ≥ 28
Составить программу-генератор простых чисел, в основу положить формулу 2*(x)^2 + 29 при 0 ≥ х.
Решение
Каким образом задаётся число m? Оно должно быть зашито в программу или записано в виде строки на ленте?
Какова система кодировки? Обычная единичная система счисления?
Насчёт последовательного вычисления квадратов могу дать такую наводку. Каждый квадрат — это сумма последовательных нечётных чисел.
1 = 1
4 = 1+3
9 = 1+3+5
16 = 1+3+5+7
.
Примерно так я себе представляю получение, например, из квадрата тройки квадрат четвёрки.
Пусть у нас имеется квадрат тройки в таком виде:
221121111
количество символов равно самому квадрату, с двойки начинается очередное нечётное число.
Копируем эту строку через пробел (надеюсь, вы умеете это делать, если не умеете, спросите меня как):
221121111 221121111
Затем копируем в конец последней строки её же собственную подстроку, начиная с последней двойки
221121111 22112111121111
Затем приписываем в конец ещё две единицы
221121111 2211211112111111
Всё, 16 получили, дальше таким же макаром получаем 25.
Там есть, конечно, нюансы, которые я опустил. Например, в конце процесса нужно пройтись через всю шеренгу назад и заменить двойки на единицы. При копировании строк придётся тоже переименовывать ячейки, чтобы не сбиться со счёта.
В общем, задачка у вас весёлая. Но всё же легче, чем писать на машине Тюринга компилятор языка C# :
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Машины Тьюринга
| Заслуженный участник |
| Последний раз редактировалось Deggial 16.11.2013, 09:37, всего редактировалось 1 раз. |
| формулы поправил |
А что это за вид? Обычно же вид такой: 
Последний раз редактировалось cool.phenon 10.05.2013, 11:55, всего редактировалось 1 раз.
Этот вид предложил преподаватель, впоследствии такой же я обнаружил в учебнике «Введение в дискретную математику» Яблонского.
Ну тут тоже вроде похоже, только вместо 
А вот тут можно поподробнее? Не очень понятно, как это конкретно делается. Вообще не понятно, как на этом языке реализовать условие. Предполагаю
A вот умножать- что- то совсем глухо. Не могли бы вы поподробнее объяснить?
| Заслуженный участник |
Последний раз редактировалось Sonic86 10.05.2013, 13:55, всего редактировалось 1 раз.
Так, я домыслю: 


| Заслуженный участник |
Лента бесконечная в обе стороны, здесь считается, что считывающая головка стоит в начале (на первой единице), то есть, искать начало не нужно, что уже хорошо.
Вот, попробовал нечто другое.
Сложение на 1 бесконечной ленте я знаю, 2 группы единичек разделены нулём, нуль заменяем на 1, идём в самый конец и убираем 1 единицу.
Но вот тут у меня проблема, допустим, сложил один раз, но дальше мне уже нужно знать, сколько именно единиц слева или справа нужно приписать, а этого в машине Тьюринга никак не напишешь. Что здесь можно сделать?
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
| Заслуженный участник |
Последний раз редактировалось Sonic86 10.05.2013, 17:39, всего редактировалось 4 раз(а).
А зачем писать запятые?
| Заслуженный участник |
Последний раз редактировалось cool.phenon 10.05.2013, 18:24, всего редактировалось 3 раз(а).
| Заслуженный участник |
(О структурном подходе.)

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Машина тьюринга возведение в квадрат
Нечасто гипотетические механизмы, существовавшие только в воображении автора, становились фундаментом грандиозных перемен. Машине Тьюринга, абстрактной математической модели алгоритмов, это удалось в полной мере, а 24‑летний британский математик, фактически предсказав устройство и логику всех вычислительных машин нашего времени, невольно стал отцом информационных технологий, полностью изменивших мир.
Эта статья была опубликована в журнале OYLA №9(37). Оформить подписку на печатную и онлайн-версию можно здесь.
Наша жизнь буквально пронизана всевозможными инструкциями и алгоритмами, ведь если вдуматься, жизненный опыт — это сумма усвоенных алгоритмов: чем их больше, тем легче в разных условиях добиться желаемого результата. А большая часть физиологических процессов в нашем теле, таких как дыхание и пищеварение, настолько автоматизированы, что организм выполняет их с точностью прописанной программы. Не делает ли это нас подобием машин? От этой мысли совсем недалеко до принятия концепции детерминизма. Согласно ей, мир — это сложная, но всё же машина, работающая на основе простых физических законов. Следовательно, взаимодействие этих машин подчинено причинно-следственной связи: зная совокупность причин, можно однозначно предсказать исход события. Например, если говорить о движении небесного тела вокруг звезды, то, зная массу, начальную скорость объектов и всемирный закон тяготения Ньютона, можно с большой точностью предсказать местоположение этого объекта в любой момент его существования.
Подобных взглядов придерживался великий французкий математик Пьер-Симон Лаплас. В 1814 году, описывая мысленный эксперимент, он предложил представить гипотетическое существо (наречённое позже демоном Лапласа), способное абсолютно точно предсказать все события во Вселенной на основе знания о положении и скорости всех её частиц. Приведём рассуждение учёного:
«Мы можем рассматривать настоящее состояние Вселенной как следствие его прошлого и причину его будущего. Разум, которому в каждый определённый момент времени были бы известны все силы, приводящие природу в движение, и положение всех тел, из которых она состоит, будь он также достаточно обширен, чтобы подвергнуть эти данные анализу, смог бы объять единым законом движение величайших тел Вселенной и мельчайшего атома; для такого разума ничего не было бы неясного и будущее существовало бы в его глазах точно так же, как прошлое».
Лаплас предполагал, что Демон будет оперировать законами классической механики. Но последующие открытия в физике показали, что законы Вселенной намного сложнее механики Ньютона. Термодинамическая необратимость и законы неопределённости в квантовой механике опровергают даже гипотетическую возможность существования Демона. Из чего следует, что наш мир не настолько детерминирован. Несмотря на это, именно детерминизм оказал сильнейшее влияние на научный метод, ведь он подталкивал учёных искать первопричину тех или иных явлений.
Спустя столетие подобными вопросами задался кембриджский студент Алан Тьюринг. Ещё в школьные годы он решал сложные математические задачи и самостоятельно освоил такие непростые дисциплины, как дифференциальное и интегральное исчисления. Математика стала его истинной страстью, и Тьюринг с радостью вступил в ряды её ревностных служителей. С наставником Алану тоже повезло: им вызвался быть талантливый математик Годфри Харди, видевший в древней науке такую же красоту, как на полотнах Леонардо и в сонетах Шекспира. Кстати, Харди считал своим величайшим достижением не работы по теории чисел, а открытие миру гениального индийца Сринивасы Рамануджана, который самостоятельно, без специального образования и общения с профессорами, дошёл до вершин математической науки.
Вернёмся к Тьюрингу. С таким замечательным наставником Алан всё чаще вспоминал отрывок из прочитанной в детстве книжки популяризатора науки Эдвина Тенни Брюстера «Чудеса природы, о которых должен знать ребёнок»:
«Человеческое тело представляет собой машину. Очень замысловатую машину с гораздо, гораздо более сложным устройством, чем у любой другой, созданной человеком, но всё-таки машину».
В машине теоретически можно определить всё: количественное взаимодействие частей, поведение в прошлом, настоящем и, главное, в будущем. Кроме того, раз можно рассчитать все мыслимые параметры для одной машины, то почему бы не сделать это для десятка? Для миллиона? Триллиона, наконец? Вспомним детерминизм Лапласа.
На практике дело упирается лишь в вычислительную мощь устройства расчёта и необходимое для него время. А что мы понимаем под словом «расчёт»? Формально это последовательность некоторых операций над некими символами (числами и буквами). Причём заданная последовательность операций — не что иное, как алгоритм. Например, нам необходимо рассчитать значение функции f(x, y) = x²+ y² для некоторых x и y. Мы видим следующие символы: x, y, 2, +. И два вида операций: возведение в квадрат и сложение. А ведь все действия, подумал Тьюринг, в конечном счёте сводятся к нескольким элементарным: считать символ, произвести операцию, записать результат и перейти к следующему действию. Все эти расчёты умела делать машина Тьюринга, более того, на её базе можно было составлять алгоритмы. Хотя Тьюринг описывал свою машину как абстрактную, она имеет достаточно механическое воплощение. Об этом и поговорим далее.
Самодостаточна ли математика?
Вы наверняка слышали фразу, что решить можно любую задачу, главное — правильно сформулировать условия. Немецкий математик Давид Гильберт, чьи работы оказали колоссальное влияние на математику XX века, вообще считал, что «в математике не может быть неразрешимых проблем». Он перечислил 23 задачи, требующие решения, полагая, что объединёнными усилиями с ними удастся справиться. До сих пор решена только часть из них, а из семи так называемых задач тысячелетия, сформулированных Математическим институтом Клэя в 2000 году, вообще решена только одна.
Если есть задачи, решение которых затруднительно в рамках существующих методов, то, может, есть и такие, которые решить алгоритмически вообще невозможно? Об этом задумался австрийский математик и философ Курт Гёдель, сформулировавший и доказавший знаменитую теорему о неполноте, смысл которой в самом простом изложении таков: в рамках заданной символьно-логической системы (учёный взял в качестве примера арифметику и теорию множеств) есть такие утверждения, которые нельзя ни опровергнуть, ни подтвердить средствами этой системы.
Теперь давайте рассмотрим простую интерпретацию этой теоремы. Представим компьютер, который работает строго логически. Согласно теореме Гёделя, существует утверждение, истинность или ложность которого этот компьютер не сможет проверить, потому что сама аксиоматика логики, основного принципа его работы, неполна. Британский математик Роджер Пенроуз использовал этот довод для демонстрации принципиальной разницы между мозгом человека и компьютера. Последний, в отличие от человека, неспособен осознать неполноту.
На идею о механизме Тьюринга натолкнула пишущая машинка. Казалось бы, при чём здесь машинопись? Не вдаваясь в детали конструкции и особенности привода (ручного или электрического), пишущая машинка — это устройство работы с символами: буквами, цифрами, знаками препинания и т. д. На каждое нажатие клавиши она отвечает строго определённым образом, переходя в одно из возможных состояний — верхний или нижний регистры, соответствующие прописным или строчным буквам.
К моменту набора очередного символа оператор сравнивает текущее и необходимое состояние устройства. Если они совпадают, то всё в порядке, если же нет — от оператора требуется перевести машину в другой регистр. Элементарно? Конечно! Но вот что интересно: можно было совершенно точно сказать, в каком состоянии будет находиться старенький, но исправный «ремингтон» в момент, когда напечатают последний символ текста.
А что, если объединить оператора и пишущую машинку в автоматического исполнителя алгоритмов? Ведь на базовом уровне всё соответствует: обрабатываемые символы, алгоритм действий, разные состояния. А ещё каретка машинки могла перемещаться и печатать символы в любом месте листа, то есть устройство срабатывало в произвольной, но корректной в заданных условиях позиции. Механизм, придуманный Тьюрингом, был аналогом пишущей машинки, но более универсальным и не требующим присутствия и вмешательства человека. Гипотетический агрегат обладал заданным числом конфигураций-состояний и однозначно (это важно) срабатывал в каждом из них.
Лента. Чтобы не распыляться на технические детали вроде валика для протяжки бумаги, Тьюринг для своей машины выбрал простейший вариант: рабочая поверхность представляла собой бесконечную ленту, разбитую на клетки, в каждую из которых впечатывается (или стирается) один символ. На этой ленте изначально записывается некоторое выражение, которое требуется рассчитать. То есть она используется для хранения информации.
Каретка. Каретка свободно перемещается влево и вправо на неограниченное количество позиций. Существенное отличие от пишущей машинки заключалось в том, что каретка могла «сканировать» (по выражению самого Тьюринга) информацию в клетке и при необходимости стирать её. Обработав ячейку, каретка смещается на следующую позицию.
Машина Тьюринга — агрегат «умный», обходится без помощи человека. В зависимости от комбинации отсканированного символа и собственной конфигурации (помните регистры у пишущей машинки?) она выполняет следующие действия:
В результате по заданному на ленте набору символов машина Тьюринга должна выдать некий результат и прекратить работу.
Давайте создадим машину Тьюринга, которая будет складывать два натуральных числа N и M, а результат, как и исходные числа, — записывать на ленте в виде последовательности единиц. Каретка находится в самой левой части ленты (в месте, обозначенном как ↓).
Для наглядности приведём пример результата работы машины Тьюринга для задачи 4 + 3 = 7:
Все состояния машины можно занести в таблицу-инструкцию. Машина начинает работу с состояния q₀ и заканчивает в состоянии q₅.
Поменяйте что-нибудь в таблице — и вы получите другую машину! А так как изменения можно вносить бесконечно, то и машин будет множество. Правила перехода можно сделать такими, что машина Тьюринга превратится в универсальный автомат, способный выполнять арифметические операции, искать определённые символы, вычислять тригонометрические функции, наконец, останавливать работу, достигнув так называемой терминальной конфигурации. Такой «всеядности» способствует простейшее обстоятельство: цифры тоже символы, а значит, машине Тьюринга подвластны не только буквы, но и сложнейшая математика.
Машина Тьюринга
Содержание
Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.
Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:
При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.
Определение [ править ]
Определение машины [ править ]
Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.
Определение процесса работы [ править ]
Особо следует рассмотреть случай переходов по пробельному символу:
Для машины Тьюринга, которая пишет символ [math]B[/math] на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.
Результат работы [ править ]
Примеры машин-распознавателей и машин-преобразователей будут даны ниже.
Примеры машин Тьюринга [ править ]
Прибавление единицы [ править ]
Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:
| [math]0[/math] | [math]1[/math] | [math]B[/math] | |
| [math]S[/math] | [math]\langle R, 1, \downarrow \rangle[/math] | [math]\langle S, 0, \rightarrow \rangle[/math] | [math]\langle R, B, \leftarrow \rangle[/math] |
| [math]R[/math] | [math]\langle R, 0, \leftarrow \rangle[/math] | [math]\langle R, 1, \leftarrow \rangle[/math] | [math]\langle Y, B, \rightarrow \rangle[/math] |
Проверка того, является ли слово палиндромом [ править ]
| [math]0[/math] | [math]1[/math] | [math]B[/math] | |
| [math]S[/math] | [math]\langle F_0, B, \rightarrow \rangle[/math] | [math]\langle F_1, B, \rightarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]F_0[/math] | [math]\langle F_0, 0, \rightarrow \rangle[/math] | [math]\langle F_0, 1, \rightarrow \rangle[/math] | [math]\langle B_0, B, \leftarrow \rangle[/math] |
| [math]F_1[/math] | [math]\langle F_1, 0, \rightarrow \rangle[/math] | [math]\langle F_1, 1, \rightarrow \rangle[/math] | [math]\langle B_1, B, \leftarrow \rangle[/math] |
| [math]B_0[/math] | [math]\langle R, B, \leftarrow \rangle[/math] | [math]\langle N, 1, \downarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]B_1[/math] | [math]\langle N, 0, \downarrow \rangle[/math] | [math]\langle R, B, \leftarrow \rangle[/math] | [math]\langle Y, B, \downarrow \rangle[/math] |
| [math]R[/math] | [math]\langle R, 0, \leftarrow \rangle[/math] | [math]\langle R, 1, \leftarrow \rangle[/math] | [math]\langle S, B, \rightarrow \rangle[/math] |
Варианты машины Тьюринга [ править ]
В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.
Многодорожечная машина Тьюринга [ править ]
Машина Тьюринга с полубесконечной лентой [ править ]
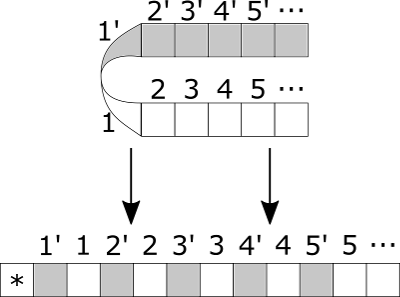
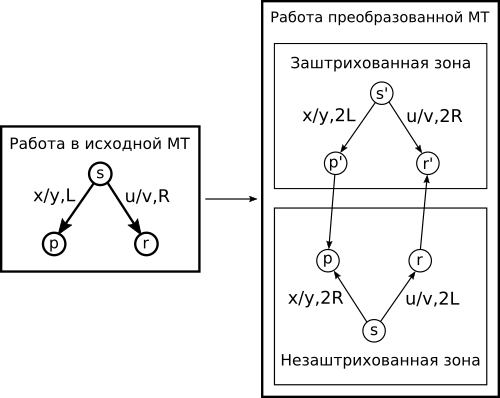
Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.
Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом:
Затем перенумеруем ячейки, и запишем символ [math]c \in \Pi \setminus \Sigma, B[/math] в начало ленты, который будет означать границу рабочей зоны:
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации.
Многоленточная машина Тьюринга [ править ]
Многоленточная машина с [math]n[/math] дорожками эмулируется многодорожечной машиной с [math]2n[/math] дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом [math]*[/math] позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).
Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов [math]*[/math] символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.
Аланом Тьюрингом было сформулировано следующее утверждение: