Машины с неограниченными регистрами определение
Алгоритмы для исполнителя МНР
(машины с неограниченными регистрами)
Опишем исполнителя МНР. МНР состоит из памяти данных и программной памяти. Ячейки памяти данных называют регистрами и обозначают R0, R1, R2 и т.д. до бесконечности. В каждом регистре может содержаться любое целое неотрицательное число. Число, содержащееся в Rn, или значение регистра Rn будем обозначать rn. В каждый момент времени только конечное число регистров содержит какие-то числа, т.е. память данных является не бесконечной, а потенциально бесконечной. МНР работает по программе. Программой называется пронумерованная конечная последовательность команд, хранящаяся в программной памяти. Программная память МНР также является потенциально бесконечной. Будем считать, что во всех ячейках, свободных от команд программы записана специфическая команда – Stop, результатом исполнения которой является остановка выполнения программы.
Система команд МНР содержит следующие команды:
1. Команда обнуления.
Команда обнуления записывается Z(n). Команда Z(n) выполняется так: содержимое регистра Rn обнуляется, т.е. rn становится равным нулю (rn:=0), содержимое других регистров не изменяется.
Пример 5. Пусть начальная конфигурация МНР имеет вид:
МНР выполнит команду обнуления – Z(3). Результатом будет следующая
2. Команда прибавления единицы.
Команда прибавления единицы имеет вид S(n). Команда S(n) выполняется так: содержимое регистра Rn увеличивается на единицу, т.е. rn:=rn+1, новое значение rn равно старому значению, сложенному с 1, содержимое других регистров не изменяется.
Пример 6. Пусть начальная конфигурация МНР имеет вид (*). МНР выполнит команду S(4). Тогда новая конфигурация имеет вид:
3. Команда переадресации.
Команда переадресации имеет вид T(m,n). Команда T(m,n) выполняется так: содержимое регистра Rn заменяется числом rm, содержащимся в регистре Rm, т.е. rn:=rm, содержимое других регистров (включая Rm) не изменяется.
Пример 7. Пусть начальная конфигурация МНР имеет вид (**). МНР выполнит команду T(4,2). Тогда новая конфигурация МНР имеет вид:
В МНР есть особый регистр, который назовем счетчиком адресов команд (САК). При запуске программы на выполнение в САК заносится 1. Выполнение каждой команды МНР состоит из четырех этапов:
1. Читается адрес из САК.
2. Запоминается команда из памяти по этому адресу.
3. САК увеличивается на единицу.
4. Выполняется запомненная команда.
МНР выполняет каждую команду программы в 4 этапа, пока не встретит команду Stop.
Команды обнуления, прибавления единицы и переадресации называются арифметическими. После каждой команды типа 1-3 выполняется команда со следующим номером.
4. Команда условного перехода.
В работе алгоритма могут быть моменты, когда предписываются альтернативные действия, зависящие от результата работы алгоритма к этому моменту. В других ситуациях может потребоваться повторить группу команд несколько раз. МНР может выполнять такие процедуры, используя команды условного перехода; они позволяют делать скачки вперед и назад в списке команд. Мы будем использовать команду условного перехода для совершения, например, следующего действия: «Если r2=r6, перейди к десятой команде программы, в противном случае, перейди к следующей команде программы». Команда, вызывающая это действие, записывается как J(2,6,10).
Команда условного перехода в общем виде записывается так J(m,n,q). Выполнение команды осуществляется следующим образом: сравнивается содержимое регистров Rm и Rn, если rm=rn, то МНР переходит к выполнению q-ой команды исполняемой программы, в САК заносится число q; если rm¹rn, то МНР переходит к выполнению команды, следующей в программе за J(m,n,q), САК увеличивается на единицу, содержимое регистров не изменяется. Если условный переход невозможен ввиду того, что в исполняемой программе команд меньше, чем q, то МНР прекращает работу.
С помощью данной команды можно осуществлять и безусловный переход. Для этого команду нужно записать следующим образом: J(m,m,q).
Работа на МНР состоит из следующих этапов:
1. Заполняем регистры памяти данных какими-то числами, т.е. задаем так называемую начальную конфигурацию.
2. Заполняем командами ячейки программной памяти.
3. Записываем в САК единицу, запускаем МНР и она работает так, как было описано выше до тех пор, пока не встретит команду Stop. При этом полученное по окончании работы машины содержимое регистров памяти данных называется конечной конфигурацией.
Задача 37. Напишите для исполнителя МНР алгоритм вычисления суммы целых положительных чисел x и y, результат запишите в регистр R0.
Решение. Поместим x в регистр R0, y – в регистр R1, т.е. зададим начальную конфигурацию:
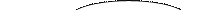
Исполнение алгоритма при x=3, y=2
Исполнение алгоритма представим в виде последовательности состояний конфигурации МНР после исполнения очередной команды.
| Шаги | САК | Исполняемая команда | Конфигурация МНР после исполнения команды | Проверяемое условие |
| R0 | R1 | R2 | R3 | |
| … | … | |||
| Z(2) | … | |||
| J(1,2,6) | … | 2=0 (нет) | ||
| S(0) | … | |||
| S(2) | … | |||
| J(0,0,2) | … | 4=4 (да) САК=2 | ||
| J(1,2,6) | … | 2=1 (нет) | ||
| S(0) | … | |||
| S(2) | … | |||
| J(0,0,2) | … | 5=5 (да) САК=2 | ||
| J(1,2,6) | … | 2=2 (да) САК=6 | ||
| Stop |
Задача 38. Напишите для исполнителя МНР алгоритм определения является ли треугольник с заданными сторонами a, b, c равнобедренным: 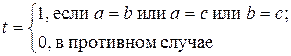
Решение. Зададим начальную конфигурацию:
Алгоритм вычисления t:
Исполнение алгоритма при a=5, b=4, c=4
| Шаги | САК | Исполняемая команда | Конфигурация МНР после исполнения команды | Проверяемое условие |
| R0 | R1 | R2 | R3 | |
| … | ||||
| Z(3) | ||||
| J(0,1,6) | 5=4 (нет) | |||
| J(0,2,6) | 5=4 (нет) | |||
| J(1,2,6) | 4=4 (да) САК=6 | |||
| S(3) | ||||
| T(3,0) | ||||
| Stop |
| R0 | R1 | R2 | … |
| x | y | z | … |
Задача 39.Напишите для исполнителя МНР алгоритм нахождения большего из трех целых положительных чисел t = max(x,y,z). Результат запишите в регистр R0.
Решение. Зададим начальную конфигурацию:
Немного логики…
Задача #2 «Позитивные автоматы»
Для тех, кто не хочет читать:
Найти значение выражения: |x — |y||
X, Y — любые целые ( и отрицательные тоже )
Ограничение: нельзя пользоваться sub, dec… и любое другое вычитание, нельзя пользоваться регистрами флагов и бинарными операциями. (в частности сдвигами)
Все что у вас есть: je, cmp (нельзя смотреть флаги), jmp, inc, mov. (я же сказал, немного)
Для того, что бы лучше разобраться в задаче:
Есть такая замечательная штуковина, называется:
Машина с неограниченными регистрами (МНР)
Итак, зачем это? Лично для меня — расшевелить мозги.
Теперь попробуем в деле!
Как ей можно пользоваться? Пример: сложите два числа, в R0-первое число, в R1-второе число. Ответ записать в R0, при том r0, r1 >= 0
Замечание: я пишу имена регистров rn, а не Rn, и имена команд тоже маленькими, имхо удобнее.
Решение:
с1) s(r0); x = x+1
c2) s(r2); r2 = r2+1
c3) j(r2,r1,c1); если r2=r1, тогда прыгнуть на с1.
с4)
Как видно, если не произойдет прыжок на метке c3, то программа остановиться и в регистре r0 будет ответ.
Ограничения:
— прыгать можно только на метки (нельзя делать адрес переменным)
— класть в регистры отрицательные числа
Если на МНР писать большие программы (например ОС), удобно сделать эквивалентные команды для ассемблера (тестирование).
Заметка:
r0. rn — это зарезервированные в памяти слова. Пример: r0 dw 0
При том все «регистры» сначала в нуле.
МНР команды / АСМ. эквивалент
T(r1,r2) mov ax,r2
mov r1,ax
J(r1,r2,c1) mov ax,r2
cmp r1,ax
je c1
В общем идея: завязать себе правую руку на ноге, склеить 3 пальца на левой руке и пойти прогить на асме. Ну ничего, у нас целые 4 команды.
Хватит теории, пора задачи решать.
Задача 1. Найти ошибку в моем примере.
Задача 2. Вычесть одно число из другого, при том первое больше. r0 — первое, r1- второе. Результат в r0
Задача 3. Найти значение выражения: |x — |y||
X, Y — любые целые ( и отрицательные тоже )
r0 — x; r1-y. Результат записать в r0. В комментариях привести аналог на ассемблере или на МНР.
Машины с неограниченными регистрами
Использование механических вычислительных процессов для решения однотипных задач. Составляющие машины с неограниченными регистрами. Отражение команд обнуления, прибавления единицы и переадресации. Реализация подстановки, рекурсии и минимизации.
| Рубрика | Программирование, компьютеры и кибернетика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 11.06.2020 |
| Размер файла | 95,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Министерство образование Узбекистана
Ургенчский Государственный Университет
по курсу: «Теория алгоритмов»
Тема: «Машины с неограниченными регистрами»
Выполнил: Режепов Нуршод
Проверил: Мадатов Х
1. Машина с неограниченными регистрами (МНР)
2. Соединение программ
3. МНР-вычислимость частично рекурсивных функций
3.1 Реализация подстановки на МНР
3.2 Реализация рекурсии на МНР
3.3 Реализация минимизации на МНР
3.4 Основной результат
машина неограниченный регистр вычислительный
Машина с неограниченными регистрами является исполнителем, представляющим собой простой «идеализированный компьютер». Идеализация состоит в том, что каждый отдельный реальный компьютер ограничен как величиной чисел, которые поступают на вход, так и размером памяти (необходимой для запоминания промежуточных результатов), МНР лишена этих ограничений. Машина с неограниченными регистрами имеет неограниченно большую память, ячейки которой будем называть регистрами и обозначать R1, R2, R3,…. Каждый регистр в любой момент времени содержит неотрицательное целое число.
1. Машина с неограниченными регистрами (МНР)
Машина с неограниченными регистрами (МНР) состоит из:
1) ленты, содержащей бесконечное число регистров, обозначаемых через R1, R2, R3, …, каждый из которых в любой момент времени содержит некоторое натуральное число. Число, содержащееся в Rn, мы будем обозначать через rn;
2) программы Р, состоящей из конечного списка команд.
Команды бывают следующих четырех видов:
обозначается также 0 Rn или rn:= 0 (читается, как rn присваивается 0);
Команды обнуления, прибавления единицы и переадресации называются арифметическими.
1) Регистры R1, R2, R3. в которых содержатся соответственно натуральные числа r1, r2, r3.
Число регистров бесконечно, но только конечное множество регистров
R1, R2. Rk содержит числа, отличные от нуля. Все остальные регистры Rk+1, Rk+2. заполнены нулями.
I1, I2. Is из следующих четырех типов команд:
* Команда обнуления Z(n) делает содержимое регистра Rn равным нулю.
* Команда прибавления единицы S(n) к содержимому регистра Rn прибавляет число 1.
* Команда переадресации T(m, n) заменяет содержимое регистра Rn на содержимое регистра Rm.
Команды обнуления, прибавления единицы и переадресации называются арифметическими командами. Отразим действие команд следующей таблицей (табл. 1).
Действие, производимое МНР
при выполнении команды
Если rn= rm, то перейти к выполнению команды с номером q, иначе выполнить следующую по порядку команду.
Таблица 1: Команды МНР
Пусть, например, регистры МНР имеют вид
Выполним команду S(2). Эта команда прибавит 1 к числу 3 в регистре R2 и не затронет остальные регистры. В результате получим следующее содержимое регистров
Выполним затем команду T(2,1). Содержимое 4 из регистра R2 заменит старое содержимое 2 в регистре R1. Получим регистры
Условие остановки. Машина останавливается тогда и только тогда, когда невозможно выполнить очередную предписанную команду. Это означает, что МНР только что совершила i-вый такт работы и следующим i+1 тактом должна выполнить несуществующую команду. Эта ситуация при выполнении программы I1, I2. Is возникает ровно в одном из трех следующих случаев.
2) Если в i-вом такте выполнена команда условного перехода J (m, n, q), где rm= rn и q > s, тогда следующим i+ 1 тактом должна выполняться несуществующая команда Iq.
Результат вычислений. Если выполнение программы завершилось, то число r1 из регистра R1 считается результатом применения алгоритма к исходному набору чисел r1, r2. Если выполнение программы никогда не заканчивается, то нет результата вычислений. В этом случае алгоритм неприменим к исходным данным. Тем самым при работе МНР возможно лишь два типа завершения работы: 1) выдача результата и 2) бесконечная работа. Третий случай (безрезультатная остановка) невозможен.
ПРИМЕР 6.1. Составить программу для МНР, которая вычисляет функцию f(x) = x +2.
Решение. Рассмотрим работу МНР со следующей программой:
ПРИМЕР 6.2. Составить программу для МНР, которая вычисляет функцию f (x, y) = x+y.
Решение. Рассмотрим работу МНР со следующей программой:
В регистр R1 перед первым тактом работы машины занесено число x,
Первый тактом работы МНР исполняется команда I1 J (2, 3, 5), где R2 сравнивается с R3, т.е. y сравнивается с числом 0.
Далее I4 задает переход к первой команде I1. Итак, МНР готова выполнить команду I=J (2, 3, 5) и совершить третий проход цикла. Однако теперь в регистрах R2 и R3 содержатся равные числа 2 и y. Тогда J(2, 3, 5) вызывает команду с номером 5. Такой команды нет. Поэтому МНР останавливается. В регистре R1 содержится результат x+ 2.
В общем случае произойдет y проходов цикла, добавляющих к числам в регистре R1 и R3 число 1. В начале y+ 1 прохода цикла в момент исполнения команды I1 J(2, 3, 5) в регистре R1 имеем x+ y, в регистре R3-число y. По команде J(2, 3, 5) МНР останавливается, имея в регистре R1 результат вычислений x+ y.
Обозначим через F множество всех функций, которые можно вычислить на подходящей машине с неограниченными регистрами.
ТЕОРЕМА 6.1. Следующие функции вычислимы на МНР.
1 Функция следования s(x).
Доказательство. Укажем программы для вычисления данных функций.
1) Функция следования s(x) имеет программу из одной команды S(1).
Действительно, если в регистре R1 занесено число x, то МНР выполнит один такт работы, сменит число x в R1 на число x+1 и остановится.
2) Аналогично программа, состоящая из одной команды Z(1), вычисляет нулевую функцию o n (x1, x2. xn).
3) Для функции проектирования (x1, x2. xn) применяем программу из одной команды T (m, 1). МНР выполнит один такт работы, перешлет в регистр R1 число xm и остановится.
Итак, все простейшие функции из определения частично рекурсивной функции вычислимы на МНР. Далее установим, что все частично рекурсивные функции вычислимы на МНР.
ОПРЕДЕЛЕНИЕ 6.2. Стандартизацией программы I1, I2. Is называется замена в данной программе всех команд J (m, n, q), где
q s+1, на команды J (m, n, s+1).
В результате стандартизации из программы P нестандартного вида получим стандартную программу P? с тем же действием. Используя P? вместо P, считаем, что все программы, которые мы рассматриваем, стандартны.
ОПРЕДЕЛЕНИЕ 6.3. Соединением программ P и Q называется программа из s+ t команд вида
где команды Is+1, Is+2. Is+t получены из команд I?1, I?2. I?t программы Q приращением номеров на число s. При этом каждая команда условного перехода J (m, n, q) из Q заменена на команду вида J (m, n, q+s).
Замена команды J(m, n, q) на команду J(m, n, q+ s) нужна по следующей причине. Номера команд из Q, когда эти команды перемещены на новые позиции в (6.1), подросли на s. Если в команде переадресации J(m, n, q) оставлен старый номер q, то вызываемой команды с таким номером q уже нет, т.к. у нее новый номер q+ s. Поэтому нужна команда J(m, n, q+s).
Соединение программ P и Q будем обозначать через PQ. Можно соединить программы P, Q, R и получить программу PQR=(PQ)R и т.д.
Выделения регистров для подпрограммы. Пусть программа P используется как подпрограмма в основной программе Q. В некоторых регистрах хранятся данные основной программы. При выполнении подпрограммы P можно испортить данные основной программы Q.
ПРАВИЛО 6.1. Пусть с=с(P) число с условием, что действие программы P меняет лишь регистры R1. Rс и не затрагивает регистры Rl для l? с. Отводим регистры R1. Rс для работы подпрограммы P, и выделяем регистры Rl при l?с в качестве рабочих регистров для остальных команд основной программы Q.
Это правило изображено в следующем виде
Если соблюдено правило выделения регистров, то программа P в процессе выполнения меняет лишь регистры R1. Rс, а данные программы Q находятся в регистрах Rс1. и не могут быть затронуты и испорчены программой P.
Вставка подпрограммы. Пусть в программе Q имеется подпрограмма P для вычисления функции f (x1. xn). В подпрограмме P имеются входные данные (x1. xn) и результат вычислений f (x1. xn). По определению МНР должны соблюдаться следующие требования.
* При старте P аргументы x1. xn обязаны находиться в регистрах R1. R1.
* После окончания работы подпрограммы P результат f (x1. xn) должен содержаться в регистре R1.
Однако в ходе работы основной программы Q возможно следующее.
Настал момент для старта подпрограммы P, которой нужны аргументы x1. xn. В данный момент аргументы хранятся в каких-то регистрах Ri1. Rin, а не в регистрах R1. Rn, как нужно. Поэтому перед применением подпрограммы P мы должны извлечь аргументы из Ri1. Rin и переслать их в регистры R1. Rn. Для осуществления такой пересылки аргументов выполняется следующее действие.
1) Перед командами из P размещается набор команд T (i1,1). T (in, n).
2) Выполняется набор команд Z (n+1). Z(с).
После выполнения подпрограммы P результат находится в регистре R1. Однако регистр R1 нужен для последующих вычислений программы Q. Поэтому из регистра R1 результат выполнения подпрограммы P нужно пересылать для его последующего использования на хранение в некоторый рабочий регистр Ri, где i? с(P). Это можно осуществить следующим способом.
3) Выполняется команда переадресации T (1, i).
Итак, для правильной работы подпрограммы P могут потребоваться следующие действия, которые назовем вставкой подпрограммы.
1) Распределение памяти. Вычисляется число с=с(P) и выделяется память R1. Rс, достаточная для работы подпрограммы P. Задается регистр Ri, где i?с, для хранения результата работы подпрограммы.
2) Извлечение аргументов. Для этого записываются следующие команды: T (i1, 1). T (in, n) для передачи аргументов из места их хранения в регистры R1. Rn.
3) Очистка регистров. Для этого записываются следующие команды:
4) Вставка команд подпрограммы P.
5) Пересылка результата на хранение. Добавляется команда T (1, i).
В итоге в основной программе получается следующий фрагмент.
Вставку данного фрагмента в основную программу обозначаем через
2. Соединение программ
Модифицированную таким образом программу P будем обозначать
3. МНР-вычислимость частично-рекурсивных функций
3.1 Реализация подстановки на МНР
Докажем, что класс всех МНР-вычислимых функций замкнут относительно операции подстановки.
G1 [m + 1, m + 2. m + n т + п + 1]
Gk[m + 1,m + 2. m + n т + п + k]
F[m + п + 1. m + п + k 1].
Действительно, вспомнив только что введенные обозначения для модифицированных программ, видим, что если в начальный момент в регистры R1. Rn помещены числа x1. хn, а в остальных регистрах содержится число 0, то в результате выполнения первых п команд программы Н числа x1. хп оказываются переписанными в регистры Rm+1,…, Rm+ n не используемые ни одной из программ F, G1. Gk.
Затем выполняется подпрограмма G1, модифицированная таким образом, что исходные данные для нее берутся из регистров Rm+1. Rm+n, а результат, если он существует, записывается в регистр Rm+n+1. В случае завершения выполнения этой программы в регистре Rm+n+1 содержится число g1(х1. хп). Затем выполняется подобным же образом модифицированная программа G2 с той лишь разницей, что результат ее выполнения записывается в регистр Rm+n+2. Вообще, если выполнение модифицированной программы Gi-1(i=2, …, k) завершилось результативно, то выполняется модифицированная программа Gi, и, в случае ее завершения, в регистр Rm+n+i помещается число gi(x1, …, xn).
Таким образом, если все значения g1(x1, …, xn). gk(x1. хп) определены, то они оказываются помещенными в регистры Rm+n+1. Rm+n+k. Затем выполняется программа F, модифицированная таким образом, что исходные данные для нее берутся из регистров Rm+n+1. Rm+n+k. Значит, эта модифицированная программа (F) вычисляет значение
т. е. значение h(x1. xn ), и, если оно определено, помещает его в регистр R1.
Таким образом, программа Н вычисляет функцию h. Следовательно, функция h является МНР-вычислимой.
3.2 Реализация рекурсии на МНР
Докажем, что класс всех МНР-вычислимых функций замкнут относительно операции рекурсии.
G[m + 1,m + 2. m + n,t + 2,t + 3 t + 3]
При у = 0 выполняется команда с номером р, которая переписывает содержимое регистра Rt+3 в регистр R1, а затем программа завершается. Таким образом, после выполнения программы в регистре R1 оказывается число f
и так далее, пока не будет получено значение h(x1. xn, у).
3.3 Реализация минимизации на МНР
Докажем, что класс всех МНР-вычислимых функций замкнут относительно операции минимизации.
Тогда программа G будет выглядеть как следующее соединение нескольких программ:
с: F[m + 1,m + 2. m + n + 1 1]
Действительно, если в начальный момент в регистры R1. Rn помещены числа x1. хn, то в результате выполнения первых п команд программы G эти числа окажутся записанными в регистрах Rm+1. Rm+n. Затем выполняется программа F, модифицированная таким образом, что исходные данные для нее берутся из регистров Rm+1. Rm+n, Rm+n+1. Заметим, что в регистре Rm+n+1 в этот момент содержится число 0. Таким образом, модифицированная программа F вычисляет значение f(x1. xn, 0) и, если оно определено, помещает его в регистр R1.
Затем содержимое регистра R1 сравнивается с содержимым регистра Rm+n+2, которое в процессе исполнения программы G остается равным нулю. Так проверяется выполнение условия f(x1. хn, 0) = 0. Если это условие выполнено, то содержимое регистра Rm+n+1, т. е. число 0, записывается в регистр R1, и программа завершается. В этом случае в регистре R1 действительно содержится значение g(х1. хп) = му[?(х1. хn, у) = 0].
© 2000 — 2021, ООО «Олбест» Все права защищены