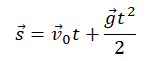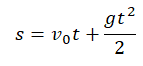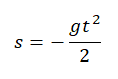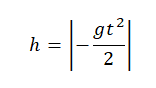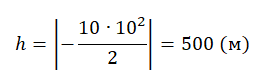На рисунке 13 изображен график движения второго автомобиля в системе отсчета

Математика 6 класс Виленкин. Номер №1445

На рисунке 132 изображены графики движения двух автомобилей: грузового (график АВ) и легкового (график CD). Определите, пользуясь графиком:

Решение а

Грузовой автомобиль вышел из города в 2 часа, а легковой в 4 часа.

Решение б

Легковой автомобиль в 4 ч 30 мин был от города на расстоянии 45 км, а в 7 ч − на расстоянии 270 км.

Решение в

Грузовой автомобиль в 4 ч был от города на расстоянии 90 км, а в 6 ч 30 мин − на расстоянии 230 км.

Решение г

Грузовой автомобиль находился на расстоянии 150 км от города в 5 ч, на расстоянии 230 км − в 6 ч 30 мин.

Решение д

Легковой автомобиль находился на расстоянии 135 км от города в 5 ч 30 мин, а на расстоянии 225 км − в 6 ч 30 мин.

Решение е

Легковой автомобиль догнал грузовой в 6 ч 20 мин на расстоянии 210 км от города.

Решение ж

Легковой и грузовой автомобиль шли с постоянными скоростями, так как график их движения − прямая линия.

Решение з

Скорость грузового автомобиля между 5 ч и 6 ч равна 195 − 150 = 45 км/ч;
его скорость между 6 ч и 7 ч равна 240 − 195 = 45 км/ч.

Решение и

В 5 ч автомобили были друг от друга на расстоянии 150 − 90 = 60 км;
в 7 ч − на расстоянии 270 − 240 = 30 км.

Источник

На рисунке 13 изображен график движения второго автомобиля в системе отсчета

МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 3. Относительность движения → номер 40 №40*(н). На рисунке 12 приведены графики движения велосипедиста I и движения мотоциклиста II в системе отсчета, связанной с землей. Написать уравнение движения велосипедиста в системе отсчета, связанной с мотоциклистом, и построить график его движения в этой …
Подробнее…

№41*(н). На рисунке 13 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движений и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения п

МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 3. Относительность движения → номер 41 №41*(н). На рисунке 13 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движений и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения первого автомобиля …
Подробнее…

№41.1(41). Скорость продольной подачи резца токарного станка 12 см/мин, а поперечной подачи 5 см/мин. Какова скорость резца в системе отсчета, связанной с корпусом станка?

МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 3. Относительность движения → номер 41 Дано: Найти v. Решение. По теореме Пифагора Ответ: v = 13 см/мин

№42. Вертолет летел на север со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует западный ветер со скоростью 10 м/с?

МЕХАНИКА. ГЛАВА I. ОСНОВЫ КИНЕМАТИКИ. 3. Относительность движения → номер 42 Дано: Найти v, α. Решение. 1). По теореме Пифагора 2) Ответ:

Источник

Задание №1 ЕГЭ по физике

В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем данные относительно Земли:

Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает вид :

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

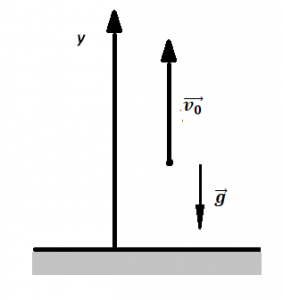
Записываем исходные данные:

Записываем формулу для определения скорости тела в векторном виде:

Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:

Подставим известные данные и вычислим скорость:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

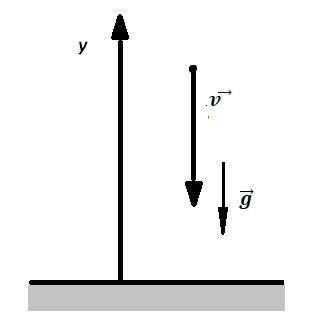
Записываем исходные данные:

Перемещение (высота) свободно падающего тела, определяется по формуле:

В скалярном виде эта формула примет вид:

Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:

Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:

Вычисляем высоту, подставив известные данные:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем исходные данные:

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

На рисунке 13 изображен график движения второго автомобиля в системе отсчета

Точечное тело равномерно движется по окружности радиусом 2 м. На рисунке изображён график зависимости угла поворота φ тела от времени t. Определите модуль линейной скорости этого тела в интервале времени 0

На рисунке показан график зависимости от времени для проекции скорости тела. Какова проекция a_x ускорения этого тела в интервале времени от 5 до 6 c? Ответ дайте в метрах на секунду в квадрате.

Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость проекции скорости V_x этого тела от времени t. Чему равен модуль изменения координаты этого тела за третью секунду движения?

Точечное тело начинает прямолинейное движение вдоль оси OX. На рисунке показана зависимость координаты x этого тела от времени t. Определите проекцию скорости этого тела на ось OX в интервале времени от 6 до 10 секунд.

Два точечных тела начинают двигаться из одной точки вдоль оси OX в противоположных направлениях. На рисунке показаны графики зависимостей проекций их скоростей V_x на ось OX от времени t. Чему будет равно расстояние между этими телами через 8 секунд после начала движения?

На рисунке приведён график зависимости проекции скорости тела v_x от времени. Чему равна проекция ускорения этого тела a_x в интервале времени от 5 до 10 с? Ответ выразите в метрах на секунду в квадрате.

На рисунке показана зависимость проекции скорости V_x точечного тела на ось OX от времени t. Определите проекцию ускорения этого тела на ось OX в интервале времени от 0 до 3 с.

Тело движется вдоль оси Оx. По графику зависимости проекции скорости тела v_x от времени t установите модуль перемещения тела за время от t₁ = 6 с до t₂ = 10 с.

Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.

Точечное тело движется вдоль оси OX. На рисунке изображён график зависимости проекции скорости V этого тела на ось OX от времени t. В момент времени t = 0 с тело имеет координату x = 10 м. Найдите координату этого тела в момент времени t = 3 с. Ответ дайте в метрах.

Материальная точка начинает двигаться по плоскости в момент времени t = 0. Её координаты x и y зависят от времени t по законам и (время измеряется в секундах, координаты — в метрах). Чему равен модуль перемещения точки за первую секунду движения?

На рисунке приведён график зависимости проекции v_x скорости тела от времени t.

Определите путь, пройденный телом в интервале времени от 0 до 5 с. Ответ приведите в метрах.

На рисунке приведён график зависимости проекции v_x скорости тела от времени t.

Определите путь, пройденный телом в интервале времени от 15 до 19 с. Ответ приведите в метрах.

Точечное тело движется вдоль оси OX. На рисунке изображён график зависимости проекции скорости V этого тела на указанную ось от времени t. В момент времени t = 0 с тело находилось в точке с координатой x₀ = 4 м. Определите координату тела в момент времени t = 3 с. Ответ дайте в метрах.

Источник

На рисунке 13 изображен график движения второго автомобиля в системе отсчета

На рисунке представлен график зависимости модуля скорости от времени t для тела, движущегося прямолинейно в инерциальной системе отсчёта.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

Это задание ещё не решено, приводим решение прототипа.

На рисунке представлен график зависимости модуля скорости от времени t для тела, движущегося прямолинейно в инерциальной системе отсчёта.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) На участке DE тело двигалось равномерно.

2) Наибольшее ускорение тело имело на участке АВ.

3) В интервале времени от 6 до 8 с тело прошло путь 6 м.

4) На участке CD кинетическая энергия тела уменьшалась.

5) В интервале времени от 0 до 2 с тело прошло путь 6 м.

Проанализируем каждое утверждение.

1) Участок DE соответствует движению с постоянной скоростью равной 3 м/c. Следовательно, утверждение верно.

2) Тело движется ускоренно на участках AB и CD. На участке AB ускорение равно а на участке CD — Следовательно, утверждение неверно.

3) В этом интервале тело двигалось со скоростью 3 м/c, следовательно, тело прошло путь 6 м.

4) Кинетическая энергия пропорциональна скорости тела. На участке CD скорость увеличивалась, таким образом, утверждение неверно.

Источник