Определить расстояние на машине между точками
Расстояние между городами
Примеры расчета расстояний:
Когда может пригодиться расчет расстояний?
Бесплатный расчет расстояний между городами показывает точное расстояние между городами и считает кратчайший маршрут с расходом топлива. Он может быть востребован в следующих случаях:
Как пользоваться расчетом расстояний?
Для того чтобы рассчитать маршрут между городами, начните вводить в поле «Откуда» название начального пункта маршрута. Из выпадающей контекстной подсказки выберите нужный город. По аналогии заполните поле «Куда» и нажмите кнопку «рассчитать».
На открывшейся странице на карте будет проложен маршрут, красными маркерами будут обозначены начальный и конечный населенные пункты, а красной линией будет показан путь по автодороге. Над картой будут указаны суммарная длина маршрута, продолжительность пути и расход топлива. Под этой информацией будет размещена сводная таблица с подробными данными о маршруте и об участках пути: тип дороги, расчетная длина и продолжительность каждого фрагмента маршрута.
Полученный маршрут можно распечатать или, изменив некоторые параметры, повторить расчет. В дополнительных настройках можно задать транзитные населенные пункты, а также скорректировать расчетную скорость движения по дорогам каждого типа. Ниже дополнительных настроек расположены поля ввода данных топливного калькулятора. Внесите в них актуальный расход горючего вашей машины и среднюю цену 1 литра топлива. При повторном расчете эти данные будут использованы для подсчета необходимого количества топлива и его стоимости.
Другие методы прокладки маршрута
Если курвиметра нет под рукой, то можно воспользоваться линейкой. Приложите нулевую отметку линейки к начальному пункту маршрута и двигайте линейку, плотно примыкая ее к извилинам дороги.
Рассчитать расстояние между городами также можно с помощью таблиц, которые опубликованы в атласах и справочниках. Это достаточно удобно для маршрутов, начинающихся и заканчивающихся в крупных городах. Мелких населенных пунктов, как правило, нет в таблицах.
Алгоритм расчета расстояния между городами
Расчет маршрута основан на алгоритме поиска кратчайшего пути во взвешенном графе автодорог (алгоритм Дейкстры). Расстояния определены по точным спутниковым координатам дорог и населенных пунктов. Расчет является результатом компьютерного моделирования, а модели не бывают идеальными, поэтому при планировании маршрута поездки не забудьте заложить резерв.
Существует несколько подходов к определению расстояния между городами:
В наших расчетах расстояния между городами берутся по автодорогам.
Рассчитать маршрут и расстояние на карте.
• Вы можете выбрать город или крупный населенный пункт из выпадающего меню, помеченного знаком ▼.
• Найти населенный пункт по почтовому Индексу:
a) Наберите «почтовый индекс» и выберите объект из выпадающего списка.
в) Наберите «почтовый индекс и страну» и нажмите кнопку «Показать».
• С помощью кнопки «Показать», вы можете найти любой населенный пункт или объект, даже если к нему невозможно построить маршрут.
• Вы можете кликать по карте, чтобы устанавливать метки, зелёная метка начало маршрута и красная метка конец маршрута.
• Вы можете удалять метки, ещё раз кликнув по ней левой кнопкой мыши.
• Вы можете перемещать по карте любую метку маршрута для изменения маршрута. Для этого нужно кликнуть мышью по метке и удерживая её нажатой, двигайть метку по карте и маршрут будет мгновенно обновляться.
• Вы можете добавлять в маршрут любое количество промежуточных меток. Для этого нужно кликать по линии основного маршрута и устанавливать новые метки. Далее, перемещая метки в нужном направлении, строить любой маршрут.
• Вы можете переключать карты, для просмотра местности в различных вариантах.
• Вы можете подробно посмотреть любую точку маршрута, кликнув по названию населенного пункта в описании маршрута в колонке слева. Маршрут включает населенные пункты в радиусе 2 км.
• Распечатать маршрут и данные на карте
Расчет маршрутов и расстояний производится без использования сторонних сервисов, по гео-данным Openstreetmap.
Расчет расстояний между городами России, Расчет маршрута и определение расстояний
Сервис определения расстояний между городами России будет полезен для планирования и расчета оптимального маршрута перед долгосрочной поездкой. Кроме, того, задавая скорость движения на различных типах дорог можно оценить время в пути. Алгоритм расчета маршрута базируется на справочной табличной информации расстояний между городами России. Не смотря на то что, расстояние между населенными пунктами является величиной относительно постоянной, тем не менее, как известно, справочные данные содержат определенную погрешность, внося не точности в общую картину расчета расстояния между городами. Это обстоятельство необходимо учитывать при планировании маршрута, а транспортным компаниям руководствоваться фактическими показаниями счетчиков пробега при расчете стоимости транспортных услуг. Обратите внимание, сервис позволяет рассчитать, как непосредственно расстояние между двумя городами России, так и через (и/или минуя) какой-либо промежуточный населённый пункт.
Удачных Вам поездок!
Проложить маршрут на основании Google карт
Обзор методов расчета расстояний между городами
С задачей определения расстояний между городами часто сталкиваются при планировании маршрута перед длительной поездкой для примерной оценки времени в пути и стоимости ГСМ.
Естественно значение расстояния по прямой линии даст весьма существенную погрешность в такие расчеты. А вот расстояние с учетом изогнутости маршрута следования будут куда более точны.
Рассмотрим основные методы определения расстояний между городами с учетом изогнутости трассы.
1. Определение расстояний по карте.
Незаменимым инструментом для определения расстояний по карте является Курвиметр. Курвиметр представляет собой портативный механический прибор с одним небольшим колесиком, которым проводят по интересующему маршруту. При этом на циферблате отображается реальное расстояние на местности в километрах. Циферблаты курвиметров могут иметь шкалы для карт разных масштабов. Обычно это масштабы 1:5000, 1:20000 и 1:50000. Курвиметр имеет метрическую шкалу.
Картографический способ нагляден и универсален, но требует не мало времени для расчета маршрута.
2. Определение расстояний по справочным таблице.
Уже достаточно давно существуют справочные таблицы расстояний между городами, позволяющие быстро получить нужную величину. Такой подход достаточно удобен, но менее нагляден. Для того чтобы продумать маршрут все равно придется воспользоваться картой. Кроме того, такие таблицы имеют весьма ограниченный перечень населенных пунктов. Если Вам нужно рассчитать расстояние от города до города, то такой метод вполне удобен.
3. Расчет расстояний с помощь специализированных программ.
В основе метода также лежат справочные данные расстояний, но прокладывание маршрута происходит автоматически. Достаточно задать название двух населенных пунктов и программа сама просчитает маршрут с указанием промежуточных точек. При необходимости можно скорректировать траекторию следования, указав населенные пункты через которые нужно проложить маршрут или наоборот – которые необходимо объехать. Некоторые программные продукты такого типа позволяют производить оценку времени пути с учетом типа трасс и возможной скорости следования по ним. Это в некоторой степени позволяет получить более точные расчетные показатели времени в пути и затрат.
Следует иметь ввиду, что не зависимо от метода расчета расстояний реальные показатели все равно будут отличны от расчетных. Поэтому при планировании поездки целесообразно все расчеты принимать во внимание с некоторым запасом, а транспортным компаниям для расчета стоимости транспортных услуг лучше пользоваться фактическими показаниями.
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Предупреждение
Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
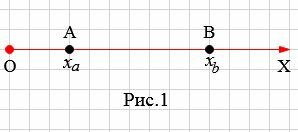 |
Расстояние между точками A и В равно:
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
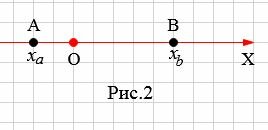 |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
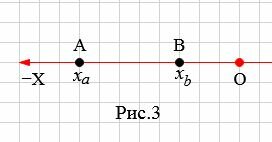 |
B этом случае рассояние между точками A и B равно:
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
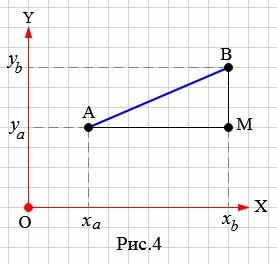 |
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
Тогда, учитывая (8), получим:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
 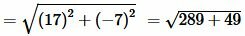 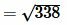 , , |
Ответ: 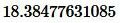
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
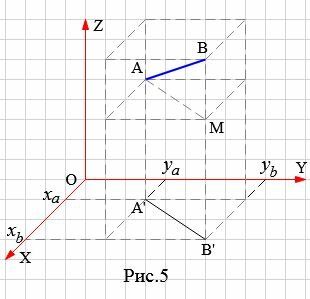 |
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
Но AM=A’B’. Тогда из (10) и (11) следует:
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
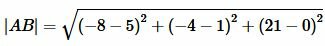 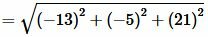 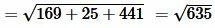 , , |
Ответ: 
Время, скорость, расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.





