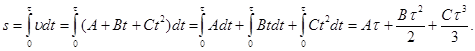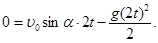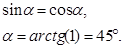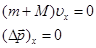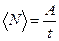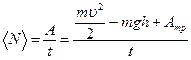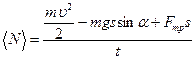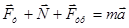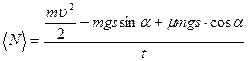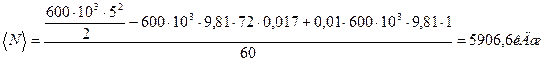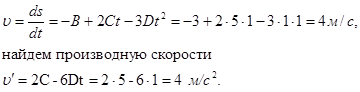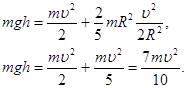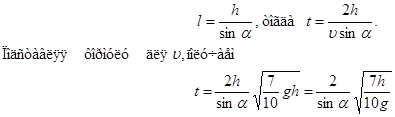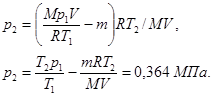По трассе в одном направлении движутся 1 и 2 автомобили
Задачи на движение в одном направлении
Рассмотрим задачи, в которых речь идёт о движении в одном направлении. В таких задачах два каких-нибудь объекта движутся в одном направлении с разной скоростью, отдаляясь друг от друга или сближаясь друг с другом.
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
Решение задачи по действиям можно записать так:
Ответ: Через 5 часов второй пешеход догонит первого.
Задача на скорость удаления
Скорость удаления — это скорость, с которой объекты отдаляются друг от друга.
Чтобы найти скорость удаления двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача. Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго — 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение: Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:
Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:
Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Два автомобиля и мотоцикл движутся по трассе в одном направлении с постоянными скоростями?
Два автомобиля и мотоцикл движутся по трассе в одном направлении с постоянными скоростями.
Когда автомобили находились в одной точке, мотоцикл отставал от них на 24 км.
Когда первый автомобиль и мотоцикл поравнялись, второй автомобиль был впереди них на 6 км.
Найдите расстояние в километрах между автомобилями в тот момент, когда мотоцикл и второй автомобиль находились в одной точке трассы.
На самом деле автомобиль 1 здесь участвует лишь для запутывания, по сути он никакой роли не играет и можно рассмотреть его не двигающимся (назовем его просто точка О), а мотоцикл и автомобиль 2 двигающимися относительно него.
Перефразируем, когда автомобиль находился в точке О, мотоцикл отставал от него на 24км.
Когда мотоцикл доехал до точки О, автомобиль был впереди него на 6км.
Найти расстояние между точкой О и автомобилем в тот момент когда мотоциклист его догонит.
За время t1 мотоциклист проехал 24км, а автомобиль 6 км, значит скорость мотоциклиста в 4 раза больше скорости автомобиля.
Если скорость автомобиля обозначить за икс, то скорость мотоциклиста будет 4x.
24 = t1 * 4x или 6 = t1 * x
Теперь представим что автомобиль не двигается, а скорость мотоцикла рассмотрим относительно него.
Скорость мотоцикла в таком случае будет 3x.
Мотоцикл догонит автомобиль (проедет 6км) на скорости 3x за время t2
Значит время t2 и t1 между собой связаны так : t1 = 3 * t2
Подставим это выражение t1 в уравнение 6 = t1 * x :
6 = 3 * t2 * x или 2 = t2 * x
А значит всего от точки О до автомобиля (и мотоцикла) будет 2 + 6 = 8км.
Решить задачу автомобиль и мотоцикл выехали одновременно в одном направлении автомобиль ехал со скоростью 75 километров час а мотоцикл 67 км какое расстояние проехал мотоцикл и автомобиль опередил его?
Решить задачу автомобиль и мотоцикл выехали одновременно в одном направлении автомобиль ехал со скоростью 75 километров час а мотоцикл 67 км какое расстояние проехал мотоцикл и автомобиль опередил его на 32 километра.
Автомобиль и мотоцикл выехали одновременно в одном направлении?
Автомобиль и мотоцикл выехали одновременно в одном направлении.
Автомобиль ехал со скоростью 75 км / ч а мотоцикл 67 км / ч какое расстояние проехал мотоцикл если автомобиль опередил его на 32км?
Автомобиль и мотоцикл выехали одновременно в одном направлении?
Автомобиль и мотоцикл выехали одновременно в одном направлении.
Автомобиль ехал со скоростью 75км \ ч, а мотоцикл 67км \ ч.
Какое расстояние проехал мотоцикл, если автомобиль опередил его на 32км?
Автомобиль и мотоцикл выехали одновременно в одном направлении?
Автомобиль и мотоцикл выехали одновременно в одном направлении.
Какое расстояние проехал мотоцикл, если автомобиль опередил его на 32км?
Задача автомобиль и мотоцикл выехали одновременно в одном направлении?
Задача автомобиль и мотоцикл выехали одновременно в одном направлении.
Автомобиль и мотоцикл выехали одновременно в одном направлении?
Автомобиль и мотоцикл выехали одновременно в одном направлении.
Автомобиль ехал со скоростью 75км / ч а мотоцикл 67км / ч.
Какое расстояние проехал мотоцикл, если автомобиль опередил его на 32км Дам 49 баллов!
Задача автомобиль и мотоцикл выехали одновременно в одном направлении автомобиль ехал со скоростью 75км / ч а мотоцикл 67км / ч какое расстояние проехал мотоцикл если автомобиль опередил его на 32км?
Задача автомобиль и мотоцикл выехали одновременно в одном направлении автомобиль ехал со скоростью 75км / ч а мотоцикл 67км / ч какое расстояние проехал мотоцикл если автомобиль опередил его на 32км.
Автомобиль и мотоцикл выехали одновременно в одном направлении?
Автомобиль и мотоцикл выехали одновременно в одном направлении.
Автомобиль ехал со скоростью 75км / ч, мотоцикл 67км / ч.
Какое расстояние проехал мотоцикл если автомобиль опередил его на 32км?
Если из этих пунктов одновременно в одно направлении ведут автомобиль и мотоцикл то автомобиль догонит мотоцикл через 5ч.
Найдите скорость автомобиля и скорость мотоцикла.
Три автомобиля движутся по шоссе в одну сторону с постоянными скоростями?
Три автомобиля движутся по шоссе в одну сторону с постоянными скоростями.
Когда первые два из них находились в одной точке, третий был на расстоянии 30 км позади них.
Когда третий автомобиль догнал второй, первый отставал от них на 6 км.
Найдите расстояние между первым и вторым автомобилями в тот момент, когда первый и третий находились в одной точке.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Задача 1.Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении



Решение. В соответствии с законом сложения скоростей υ1 = u + υ2, где υ1 – скорость первого автомобиля относительно земли, υ2 – второго, u – скорость первого автомобиля относительно второго.
Тогда скорость первого автомобиля относительно другого автомобиля будет равна разности их скоростей относительно земли, то есть
Чтобы найти скорости υ1 и υ2, необходимо найти производные пути s1 и s2 по времени.
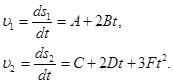
Подставляя полученные значения в выражение (1) определим относительную скорость автомобилей:
Задача 2.В течение времени τ скорость тела задается уравнением вида
υ = A + B t + C t 2 (0 ≤ t ≤ τ). Определите среднюю скорость за промежуток времени τ.
Решение. Средняя скорость определяется как отношение пути, пройденного телом ко времени движения.
По определению скорости
Для того, чтобы определить путь, пройденный телом, необходимо произвести операцию интегрирования.
Средняя скорость определяется по формуле (1)
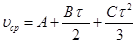
Задача 3. Для определения глубины шахты можно воспользоваться камнем и секундомером. Определить глубину шахты, если время с начала падения камня до прихода звука равнялось 5 секунд. Скорость звука в шахте принять равной 330 м/с.
Решение. Пусть время падения камня до дна шахты равно t1. Камень падает с нулевой начальной скоростью. Начало отсчета пути, пройденного камнем свяжем с точкой падения. Связь между временем падения камня до дна шахты и ее глубиной можно выразить равенством
Обозначим t2 время, за которое звук дойдет до поверхности шахты. В свою очередь, связь между временем прихода звука со дна шахты до наблюдателя и ее глубиной можно выразить следующим равенством
где υ – скорость звука в шахте. Известно, что звук доносится через некоторое время t = 5 сек от начала падения камня. За это время камень должен упасть и звук должен дойти до поверхности:
Приравнивая правые части равенств (1) и (2), найдем время падения камня до дна шахты
Получаем квадратное уравнение, одним из корней которого будет положительное значение времени t1 = 4,7 c. Подставляя полученное значение времени в выражение (1), получим высоту шахты h = 109 м.
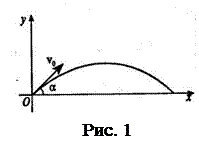
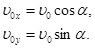
Запишем проекцию уравнения движения тела на оси х и у:
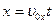
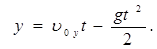
Обозначим t – время подъема тела, тогда полное время полета тела 2 t. В этот момент времени координата y = 0. Тогда из (1) и (2) получим:
И выразим отсюда время подъема тела
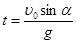
Зная время подъема, можно вычислить высоту подъема тела (как координату y в данный момент времени). Тогда, используя формулы (2) и (3) получим:
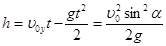
По условию задачи h = s /4. Дальность полета s будет определяться как координата x, соответствующая времени полета (2 t). Из формул (2) и (3):
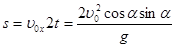
Используя соотношение h = s /4 и формулы (4) и (5) получим
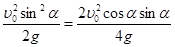
Сокращая выражение (6) получаем
Задача 5.Точкасовершает гармонические колебания с частотой
v = 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение xmax = 1 мм. Написать уравнение колебаний точки.
Решение. Уравнение колебаний точки можно записать в виде
Циклическая частота ω связана с частотой v соотношением
Для момента времени t = 0 формула (1) примет вид
Откуда начальная фаза φо = arcsin (xmax / A)=arcsin 1,
Изменение фазы на 2 π не изменяет состояния колеблющейся точки, поэтому можно принять φо = π / 2.
С учетом этих равенств, уравнение колебаний примет вид
Подставляем значения и получаем
Снаряд выпущен под углом к горизонту, следовательно, у него присутствует вертикальная составляющая импульса, которая увеличивается. Запишем этот закон в проекции на направление движения платформы и снаряда (Рис. 2).
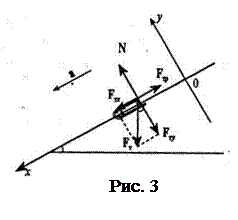
Задача 7. Поезд массой m = 600 т равноускоренно движется под гору с уклоном α = 1° (Рис. 3) и за время t = 1 мин развивает скорость υ = 18 км/ч. Коэффициент трения μ = 0,01. Определите среднюю мощность локомотива.
Решение. Средняя мощность по определению определяется по формуле
Работа представляет собой изменение кинетической энергии, потенциальной энергии, и работы сил трения.
Выразим высоту h = s sin α, а работу сил трения представим как произведение силы трения на перемещение
В соответствии со вторым законом Ньютона
Спроецировав данное выражение на ось oy, с учетом 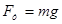
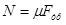
Получим, что сила трения 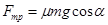
Тогда средняя мощность определяется следующим образом
Так как по условию задачи, поезд движется равноускоренно, то 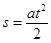
Ускорение в нашем случае будет определяться формулой
Вычислим значение работы, зная, что 18 км/ч = 5 м/с.
Решение. Определить показания весов — это значит найти вес телаG, т. е. силу, с которой тело действует на пружину. Но эта сила, по третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости N (силе реакции опоры), с которой пружина через посредство прикрепленной к ней чашки весов действует на тело, т. е.

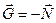
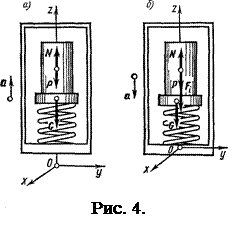
На тело действуют две силы: сила тяжести Р= mg и сила N.
Направим ось z вертикально вверх и спроецируем на нее все силы, действующие на тело. Индекс z у проекции сил опустим, так как проекции и сами силы совпадают по величине. Направление сил учтем знаком плюс или минус. Напишем уравнение движения:
Из равенств (1) и (2) следует
При вычислении показания весов следует учесть знак ускорения:
1) ускорение направлено вертикально вверх (a>0), тогда
G1 = 10∙(9,81 + 2) = 118 Н;
Решение. Величина мгновенной мощности представляет собой производную работы по времени
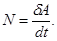
Бесконечно малая работа равна бесконечно малому дифференциалу кинетической энергии материальной точки.
Кинетическая энергия по определению равна
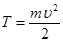
Согласно выражению (1), находим производную кинетической энергии по времени
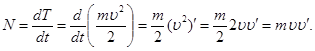
Для того, чтобы вычислить значение мощности, необходимо знать скорость движения точки, ее мы определяем по определению скорости
Тогда мощность будет равна
Задача 10. С наклонной плоскости, составляющей угол α = 30° с горизонтом, скатывается шарик. Пренебрегая трением, определите время движения шарика, если известно, что центр масс его опустился на 30 см.
Решение. В результате движения потенциальная энергия шарика mgh перешла в кинетическую энергию поступательного движения mυ 2 /2 и в кинетическую энергию вращения Jω 2 /2. Тогда, по закону сохранения энергии
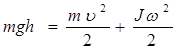
Момент инерции шара равен
где R – радиус шара, m – масса шара.
Угловая скорость связана с линейной скоростью следующим соотношением ω = υ/R.
Подставляем необходимые значения в выражение (1)
Из полученного соотношения выражаем линейную скорость движения центра масс шарика 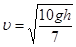
Время движения шарика можно определить из кинематического уравнения движения шарика по наклонной плоскости длинной l.
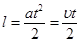
Ускорение мы определили в данном случае как a = υ/t.
Из уравнения (3) выражаем время движения шарика
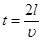
Для того, чтобы определить длину пути l шарика по наклонной плоскости воспользуемся соотношениями в прямоугольном треугольнике. Гипотенуза l будет равна
Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция Lz момента импульса системы платформа-человек остается постоянной.
Где Jz – момент инерции платформы с человеком относительно оси z,
ω – угловая скорость платформы.
Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы (платформы и человека), поэтому в начальном состоянии
а в конечном состоянии
С учетом этого равенство (1) примет вид:
где значения моментов инерции J1 и J2 соответственно относятся к начальному состоянию системы, а J’1и J’2 к конечному.
После сокращения на R 2 и простых преобразований находим скорость υ.
Тогда получим, что υ =0,94 м/с.
Решение. Запишем основное уравнение динамики вращательного движения: момент силы M равен произведению момента инерции J на угловое ускорение β.
Момент инерции шара равен
где R – радиус шара, m – масса шара.
Чтобы найти угловое ускорение, необходимо найти вторую производную от уравнения вращательного движения. Сначала найдем угловую скорость
Подставляя значения заданных физических величин, получаем, что
Знак минус показывает, что на шар действует тормозящая сила.
Задача 13. Баллон содержит m1 = 80 г кислорода и m2 = 320 г аргона. Давление смеси p = 1 МПа, температура Т = 300 К. Принимая данные газы за идеальные, определить объем баллона.
Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева-Клапейрона, парциальные давления p1 кислорода и p2 аргона выражаются формулами:
Следовательно, по закону Дальтона, давление смеси газов
Откуда объем баллона
Задача 14.В баллоне объемом 10 л находится гелий под давлением p1 = 1 МПа и при температуре Т1 = 300 К. После того, как из баллона взято m = 10 г гелия, температура в баллоне понизилась до Т2 = 290 К. Определите давление p2 гелия, оставшегося в баллоне.
Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа.
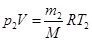
где m2 – масса гелия в баллоне в конечном состоянии, M – молярная масса гелия, R – молярная газовая постоянная.
Из уравнения (1) выразим искомое давление
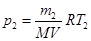
Массу m2 гелия выразим через массу m1, соответствующую начальному состоянию и массу m гелия, взятого из баллона:
Массу m1 гелия найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию:
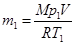
Подставив это выражение массы в (3), а затем найденное значение m2 в (2), найдем
Задача 15. Найти среднюю кинетическую энергию вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию Ек вр вращательного движения всех молекул кислорода массой m = 4 г.
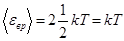
Кинетическая энергия вращательного движения всех молекул газа
Число всех молекул
где NA – постоянная Авогадро, v – количество вещества.
Если учесть, что количество вещества v = m / M, где m – масса газа,
M – молярная масса газа, то формула (3) примет вид
Подставив N в формулу (2), получим
Решение. Изменение внутренней энергии газа
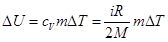
Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона pV = (m/M)RT, откуда
Работа расширения газа при постоянном давлении выражается формулой
Работа газа, нагреваемого при постоянном объеме равна нулю А2 = 0.
Следовательно, полная работа, совершаемая газом
Задача 17. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика Т1= 500 К. Определить термический КПД цикла и температуру Т2 теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу A = 350 Дж.
Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Термический КПД выражается формулой:
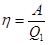
где Q1 – теплота, полученная от теплоотдатчика, А – работа, совершенная рабочим телом тепловой машины. КПД для цикла Карно выражается формулой:
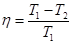
Следовательно, температура охладителя
ТАБЛИЦА ВАРИАНТОВ К КОНТРОЛЬНОЙ РАБОТЕ № 1