На рисунке представлен график зависимости скорости движения автомобиля

На рисунке представлен график зависимости скорости движения автомобиля

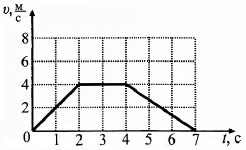
На рисунке представлен график зависимости модуля скорости автомобиля от времени t. Найдите путь, пройденный автомобилем за 5 c. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом, необходимо вычислить площадь под графиком (в единицах произведения величин, отложенных по осям координат). За 5 c автомобиль прошёл путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Здраствуйте! Я хотел бы попросить Вас подробно описать 2 способ решения. У меня почему-то не сходится.

— модуль начальной скорости

— модуль ускорения

На интервале от 0 с до 1 с равноускоренное движение:

,

Следовательно, путь равен

На интервале от 1 с до 3 с равномерное движение:

,

Путь равен

На интервале от 3 с до 5 с равнозамедленное движение:

,

Следовательно, путь равен

Итого:

почему в некоторых заданиях этого типа «за 5 секунду» означает найти путь именно за одну секунду, а в данном задании находится путь за весь промежуток??

Здесь нужно узнать путь за пять секунд, а не за пятую секунду.

Источник

На рисунке представлен график зависимости скорости движения автомобиля

На рисунке представлен график зависимости модуля скорости автомобиля от времени t. Найдите путь, пройденный автомобилем за 5 c. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом, необходимо вычислить площадь под графиком (в единицах произведения величин, отложенных по осям координат). За 5 c автомобиль прошёл путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Здраствуйте! Я хотел бы попросить Вас подробно описать 2 способ решения. У меня почему-то не сходится.

— модуль начальной скорости

— модуль ускорения

На интервале от 0 с до 1 с равноускоренное движение:

,

Следовательно, путь равен

На интервале от 1 с до 3 с равномерное движение:

,

Путь равен

На интервале от 3 с до 5 с равнозамедленное движение:

,

Следовательно, путь равен

Итого:

почему в некоторых заданиях этого типа «за 5 секунду» означает найти путь именно за одну секунду, а в данном задании находится путь за весь промежуток??

Здесь нужно узнать путь за пять секунд, а не за пятую секунду.

Источник

На рисунке представлен график зависимости скорости движения автомобиля

По графику зависимости модуля скорости тела от времени, представленного на рисунке, определите путь, пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный телом за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале времени от 0 до 2 с автомобиль прошёл путь

Примечание. В принципе, интересующий нас участок (от 0 до 2 с) не обязательно разбивать на два, площадь под графиком можно посчитать, как площадь трапеции:

В принципе, можно использовать стандартные кинематические формулы для изменения координаты, скорости, ускорения, а все необходимые данные снимать с графика. Но так получается значительно дольше.

Почему же не через площадь дольше?

S= So + vt + (at^2) / 2 т.е. S1= 0 + 0 + 2*1/2=1 ; S2= 0 + 2*1 + 0*1/2= 2 ;

Правильно. Так тоже можно.

В общем, соглашусь, что здесь правильнее говорить, что этот способ не более длинный, а скорее менее вариативный. Подсчет по формула соответствует подсчету площади как суммы фигур,соответствующих определенному типу движения (здесь у вас получился один участок с ускорением и один участок равномерного движения). Площадь же можно считать и иначе, например, сразу рассмотреть эту фигуру как трапецию.

В любом случае, как делать, это личное дело каждого, я не навязываю свое мнение 🙂

Утверждение «в первую секунду авто проехало 1 метр (т.е. оно двигалось со скоростью 1 метр в секунду)» не совсем верно, правильно тогда уж говорить так: «за первую секунду авто переместилось на такое расстояние, как если бы оно двигалось с постоянной скоростью в 1 м/с».

Однако такое утверждение в свою очередь требует разъяснений.

так путь же нужно найти почему нельзя воспользоваться формулой S=Vt

Эта формула подходит только для равномерного движения, а здесь это скорость тела изменяется

В задании не сказано, но тело двигалось прямолинейно

Решение и ответ задачи не зависят от того, двигалось ли тело прямолинейно или нет.

На рисунке представлен график зависимости модуля скорости автомобиля от времени. Определите по графику путь, пройденный автомобилем в интервале от момента времени 0 с до момента времени 5 с после начала отсчета времени. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени (в единицах произведения величин, отложенных по осям координат). В интервале от момента времени 0 с до момента времени 5 с после начала движения автомобиль прошел путь

Другой способ решения заключается в анализе каждого участка графика в отдельности, определения из графика начальных скоростей и ускорений на каждом этапе и использования стандартных кинематических формул для пути.

Источник

На рисунке представлен график зависимости скорости движения автомобиля

На рисунке представлен график зависимости модуля скорости v от времени t для тела, движущегося прямолинейно. Равномерному движению соответствует участок

Равномерное движение — это движение с постоянной скоростью. На графике зависимости скорости от времени это будет соответствовать горизонтальному участку графика, то есть участку DE. Участок BC, хотя и имеет также постоянную скорость, но при этом значение скорости на этом участке равно нулю, то есть тело покоится.

Правильный ответ указан под номером 4.

На рисунке представлен график зависимости проекции скорости v_x от времени t для тела, движущегося по оси Ox. Максимальное по модулю ускорение тело имело в интервале времени

Ускорение — скорость изменения скорости. В интервале от 1 до 3 секунд тело двигалось с постоянной скоростью, следовательно, этот интервал не подходит. Из оставшихся интервалов нам необходимо выбрать тот, на котором скорость менялась быстрее всего. Поскольку из графика видно, что движение равноускоренно, можем вычислить ускорение на каждом интервале по формуле где и скорости, соответственно, в начале и в конце интервала, а t — длина интервала.

Интервал от 0 до 1 секунд:

Интервал от 3 до 4 секунд:

Интервал от 4 до 6 секунд:

Источник

На рисунке представлен график зависимости скорости движения автомобиля

На рисунке представлен график зависимости скорости автомобиля, движущегося прямолинейно по дороге, от времени. Используя данные графика, выберите из предложенного перечня два верных утверждения и запишите в ответе цифры, под которыми они указаны.

1) Равнодействующая всех сил, действующих на автомобиль, равна нулю в промежутке времени 3-4 с

2) Ускорение движения автомобиля в промежутке времени 0-2 с меньше, чем в промежутке времени 4-7 с

3) Ускорение движения автомобиля в промежутке времени 0-2 с равно 4 м/с 2

4) Путь автомобиля за последние 3 с равен 6 м

5) Автомобиль остановился через 7 с после начала движения

В точке времени 7с скорость автомобиля равна нулю, а это свидетельствует о том, что автомобиль остановился.

На участке 2-4с автомобиль двигался с постоянной скоростью, это означает что действие всех сил было скомпенсировано.

По наклону линий можно увидеть что при разгоне автомобиль имел большее ускорение чем при торможении (по модулю конечно же)

Ну и для проверки 3его утверждения нужно воспользоваться формулой связи скорости и ускорения [math]\mathrm a=\frac<\triangle\mathrm v><\triangle\mathrm t>[/math]

Для проверки четвертого следует вспомнить формулу [math]\mathrm S=\frac<\mathrm^2>2[/math], ускорение находится по известной выше формуле.

Ответ: 15
2 1 7 5 8 6 4

Источник